图论全知识
前言
$\space\space\space\space\space$本篇的tanjan算法 我们分成两部分来进行讲解
1. 前置知识
$\space\space\space\space\space$ 在进行tanjan的讲解之前 我们需要知道一些图论的基础定义
1.图的定义
由若干个不同顶点与连接其中某些顶点的边所组成的图形就称为图。（顶点的位置以及边的曲直都是无关紧要的，而且也是没有假定这些顶点和边都要在一个平面内，只关心顶点的多少和这些变是连接哪些顶点的），通常用大写字母G表示图，V表示所有顶点的集合，E表示边的集合，记作G = (V, E)。
2.子图
如果对图G = （V, E）与G1 = （V1，E1），G1的顶点集是G的顶点集的子集，G1的边集是G的边集的子集，则G1是G的子图。
3.简单图
如果一个图没有环，并且每两个顶点之间最多只有一条边，这样的图称为简单图。
4.完全图
如果G是一个简单图，并且每两个顶点之间都有一条边，就称G为完全图。通常将具有n个顶点的完全图记为Kn。
5.二分图
如果G是一个简单图，它的顶点集合V是由两个没有公共元素的子集X = {X1，X2，……，Xn}与Y = {Y1，Y2，……，Yn}组成的，并且Xi与Xj，Yi与Yj之间没有边连接，则G称为二分图。
6.完全二分图
把图中的顶点分成两个集合，使得第一个集合中的所有顶点都与第二个集合中的所有顶点相连。
7.补图
如果G是一个N个顶点的简单图，从完全图Kn中把属于G的边全部去掉后，得到的图称为G的补图。一个图的补图的补图是本身。
8.相邻&&度数
如果图G的两个顶点Vi与Vj之间有边相连，我们就说Vi与Vj是相邻的，否则Vi与Vj不相邻。如果顶点V是边e的一个断点，就说顶点V和边e是相邻的，e是从V引出的边。从一个顶点V引出的边的条数，称为V的度数。
9.道路
在图G中，一个由不同的边组成的序列e1，e2，……，ei称为从V0到Vi的一条道路，数i称为路长，V0与Vi称为这条道路的两个端点，叫做道路的内点。
10.连通图
在无向图G中，如果从顶点V到顶点V1有路径，则称V和V1是连通的。如果对于图中任意两个顶点Vi和Vj，Vi和Vj都是连通的，则这个图称为连通图。
11.连通分量
无向图中的极大连通子图称为连通分量。
12.强连通图
在有向图G中，如果对于每一对Vi和Vj，从Vi到Vj和从Vj到Vi都存在路径，则称图G为强连通图。有向图中的极大强连通子图称为有向图的强连通分量。
2.tanjan
tarjan是一种求强连通分量、双连通分量的常用算法，其拓展例如求缩点、割点、割桥以及2-SAT等都是非常实用的
1.什么是强连通分量
在有向图G中，如果对于每一对Vi和Vj，从Vi到Vj和从Vj到Vi都存在路径，则称图G为强连通图。有向图中的极大强连通子图称为有向图的强连通分量。
如下图
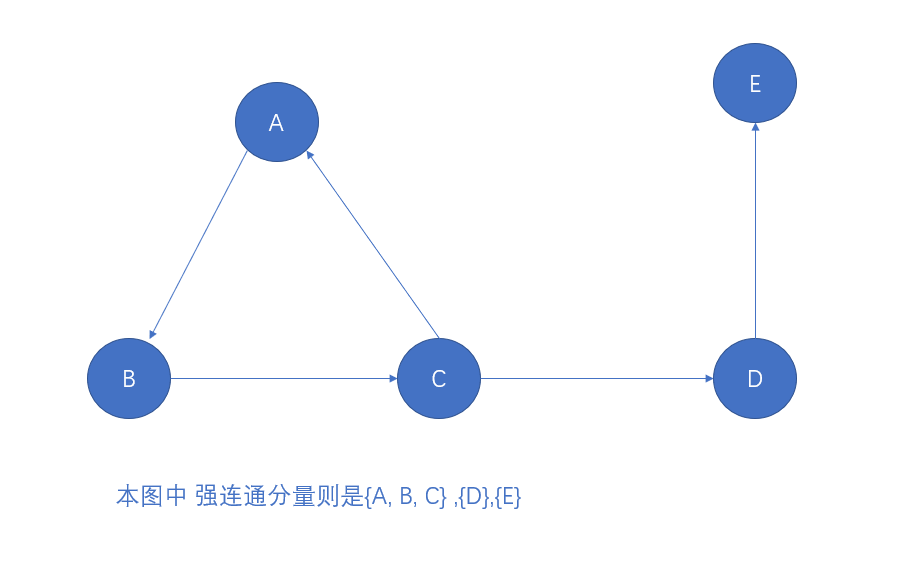
2.怎么求强连通分量
推荐视频
前置知识
树枝边：DFS时经过的边，即DFS搜索树上的边。
前向边：与DFS方向一致，从某个结点指向其某个子孙的边。
后向边：与DFS方向相反，从某个结点指向其某个祖先的边。（返祖边）
横叉边：从某个结点指向搜索树中的另一子树中的某结点的边。
$\space\space\space\space\space$我们知道tanjan是基于Dfs遍历的 过程如下
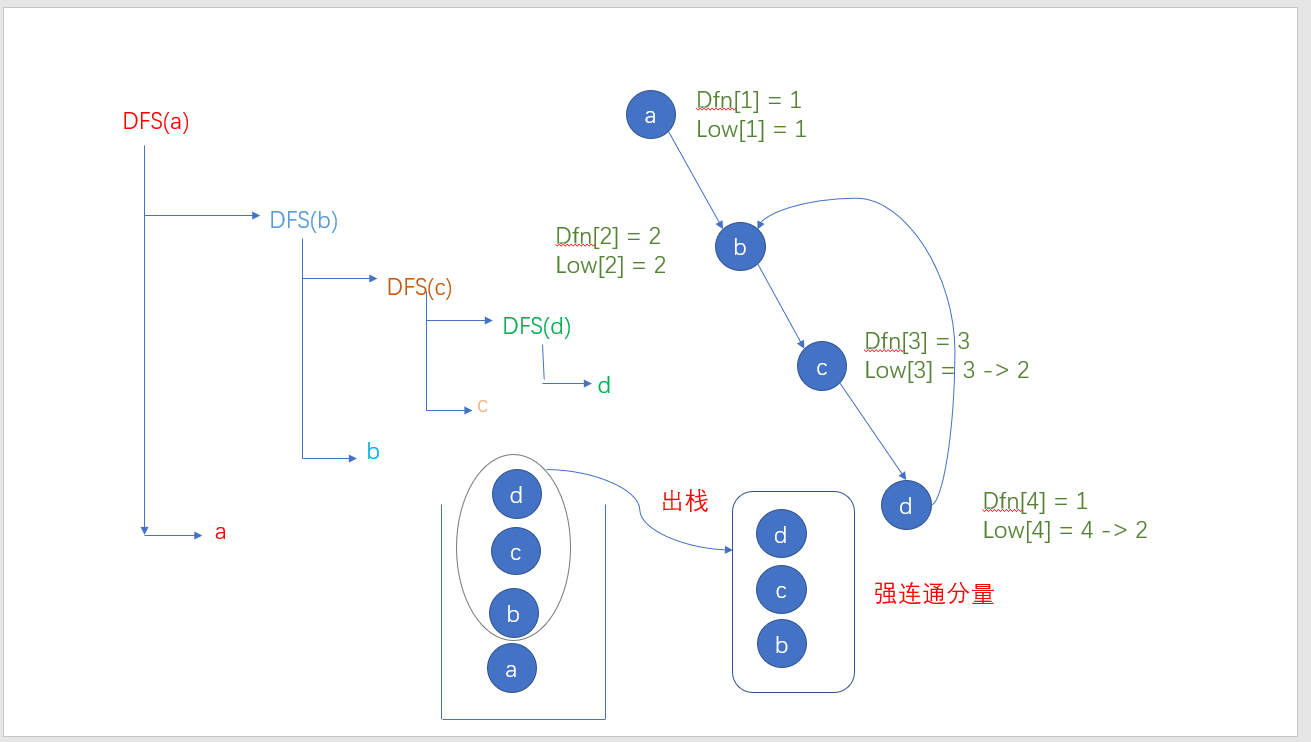
$\space\space\space\space\space$Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。 定义Dfn(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。 由定义可以得出，Low(u)= min {Low(u), Low(v) } (u,v)为树枝边，u为v的父节点 . Low(u)=Min {Low(u), Dfn(v) } DFN(v),(u,v)为指向栈中节点的后向边(指向栈中结点的横叉边) } 当结点u搜索结束后，若DFN(u)=Low(u)时，则以u为根的搜索子树上所有还在栈中的节点是一个强连通分量。
3.代码实现
我们先明确一些数组定义
dfn[ ] 表示每个点的搜索顺序 即记录每个点的时间戳
low[ ] 表示这个点所能连通的所有点中dfn最小的点
stack[ ] 数组模拟栈
in_stack[ ] boll值 记录是否在栈中
void tarjan(int u)// u当前点
{
dfn[u] = low[u] = ++ timestamp; //初始化两个数组 进行赋值
stk[++ top] = u, in_stk[u] = true; //入栈
for(int i = h[u]; i != -1; i = ne[i]) //遍历该点开始的子图
{
int j = e[i];
if(!dfn[j]) //如果没有遍历过
{
tarjan(j);//继续递归调用
low[u] = min(low[u], low[j]); // j能走到的点 u也一定能走到 更新节点信息
}
else if(in_stk[j]) //如果在当前的栈中 则属于当前的强连通分量 则进行更新节点信息
low[u] = min(low[u], dfn[j]); //更新节点u所能走到的最小编号
}
if(dfn[u] == low[u])//如果两数相等 代表强连通分量的第一个点
//要么是单独的一个点组成的强连通 要么是多个点组成的第一个入栈的点 即一个枚举起点的作用
{
++ scc_cnt;
int y;
do{
y = stk[top --]; in_stk[y] = false; //出栈
id[y] = scc_cnt;//记录所属id
Size[scc_cnt] ++; //所属"缩点"中元素+1
} while(y != u);
}
}
for(int i = 1; i <= n; i ++)
if(!dfn[i]) tarjan(i);
4.tanjan的用处
$\space\space\space\space\space$我们都知道 DAG是构成所有图类中最基础的图形 因为没有环 所以我们可以进行一系列操作 如跑Dfs 求最短路 计算方案数 搞DP 但如果是一张有向有环图 那么就不易而去处理了 因为我们这些理论都是基于DAG图
$\space\space\space\space\space$所以为了将一个有向有环图转化为DAG图 我们使用tanjan来进行缩点等一系列操作 进而等价将问题转化
$\space\space\space\space\space$简单来说 就是基于强连通分量的性质 我们可以确定该连通分量中的点对答案的贡献相同 我们就可以啥用tanjan变相将环去掉 再进行一系列操作
