1.排序算法

1.1快速排序

1.2归并排序

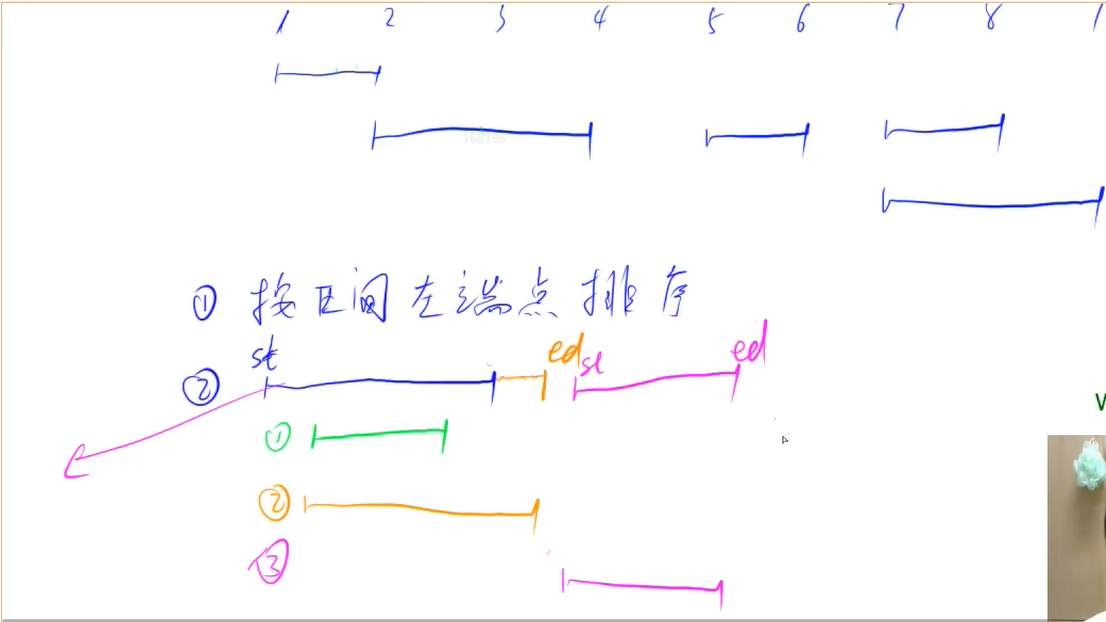
 归并和快排都是基于分治,快排是用一个具体的元素来分,归并排序是以数组下标的中间点为分界点

步骤:

• 找分界点,mid = (l + r) / 2
• 递归排序left,right
• 归并,合二为一

时间复杂度为啥是o(nlog2n)

每次都是拆分为两个一样的区间,n,(n/2,n/2).......(1,1,1...,1),可以理解为n除多少次2变为1,n / log2n = 1,
而每层都是O(n)的计算量,总共是log2n层,所以时间复杂度是o(nlog2n)

2.二分

2.1整数二分

本质,有单调性一定可以二分,可以二分的不一定有单调性.有个性质可以把整个区间一分为二,左半边满足右半边不满
足二分可以把边界给二分出来,有两个边界,所以是两个模板,一个满足性质的边界,一个不满足性质的边界

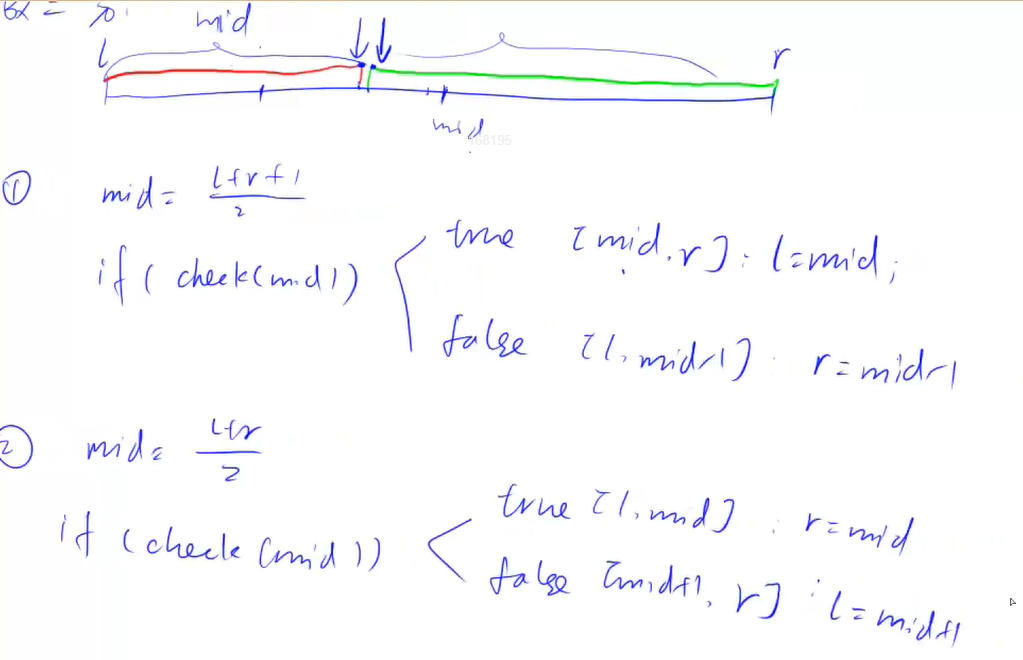
(1)为什么l+r+1,因为当l = r-1时,若不+1,则 mid = l + r >> 1  = l,当check成功后,区间没变还是[l,r]
造成死循环

(2)二分的主要思想,在一个区间内部二分我们所求的边界,每次选择区间都是选择答案所在的区间进行下一步判断

3.双指针算法

类别

1.第一类,在两个序列里面,一个指针指向第一个序列,另一个指针指向第二个序列(eg:归并排序)
2.第二类,指向一个序列(eg:快排)

用途

大概模板如下:

for(i = 0,j = 0, i < n; i++){
    while(j < i && check(i,j)) j++;
    //每道题目的具体逻辑
}

核心思想:

for(int i = 0; i< n; i++){
    for(int j = 0; j < n; j++)
    O(n^2)
}
可以将上面的朴素算法优化到O(n)

基本思路:先写一个暴力的算法,然后看枚举时,i和j之间有没有单调关系,有单调关系的话就可以把枚举数量从n^2变为n

4.位运算操作

整数n的二进制表示里,第K位数字是几

1.先把第k位数字移到最后一位 n >> k
2.看下个位是几 x & 1
3.合并 n >> k & 1

lowbit(x) :返回x的最后一位1

eg x = 1010 lowbit(x) = 10; x = 101000 lowbit(x) = 1000

5.离散化(整数离散化,保序)

值域较大,数值个数比较少,概念如下

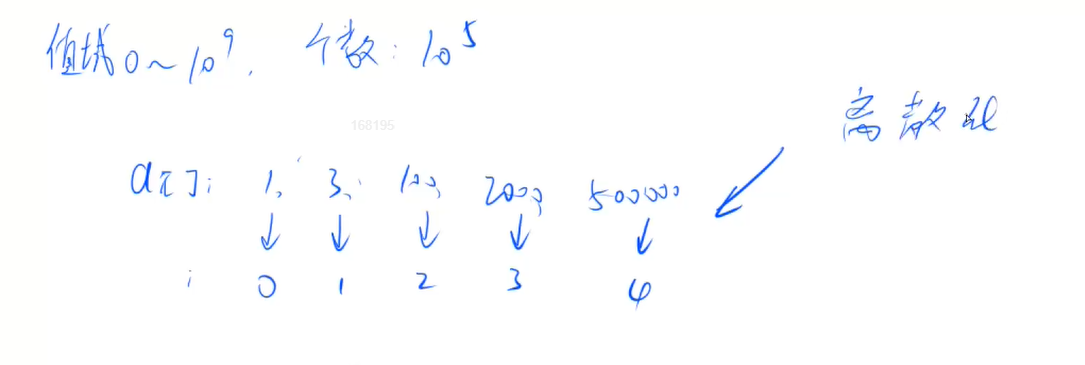
存在的问题:
1.a[]中可能有重复元素,需要去重
2.如何算出x离散化后的值 (二分)

具体实现如下

6.区间合并(贪心)

如果两个区间有交集,则合并这两个区间用一个表示