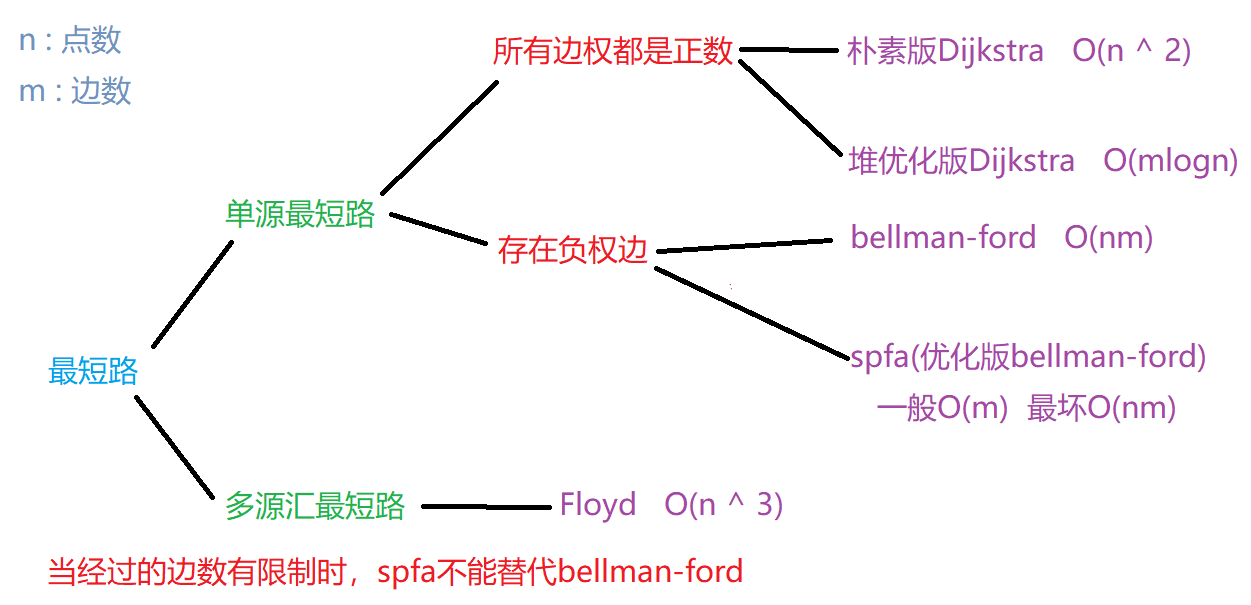
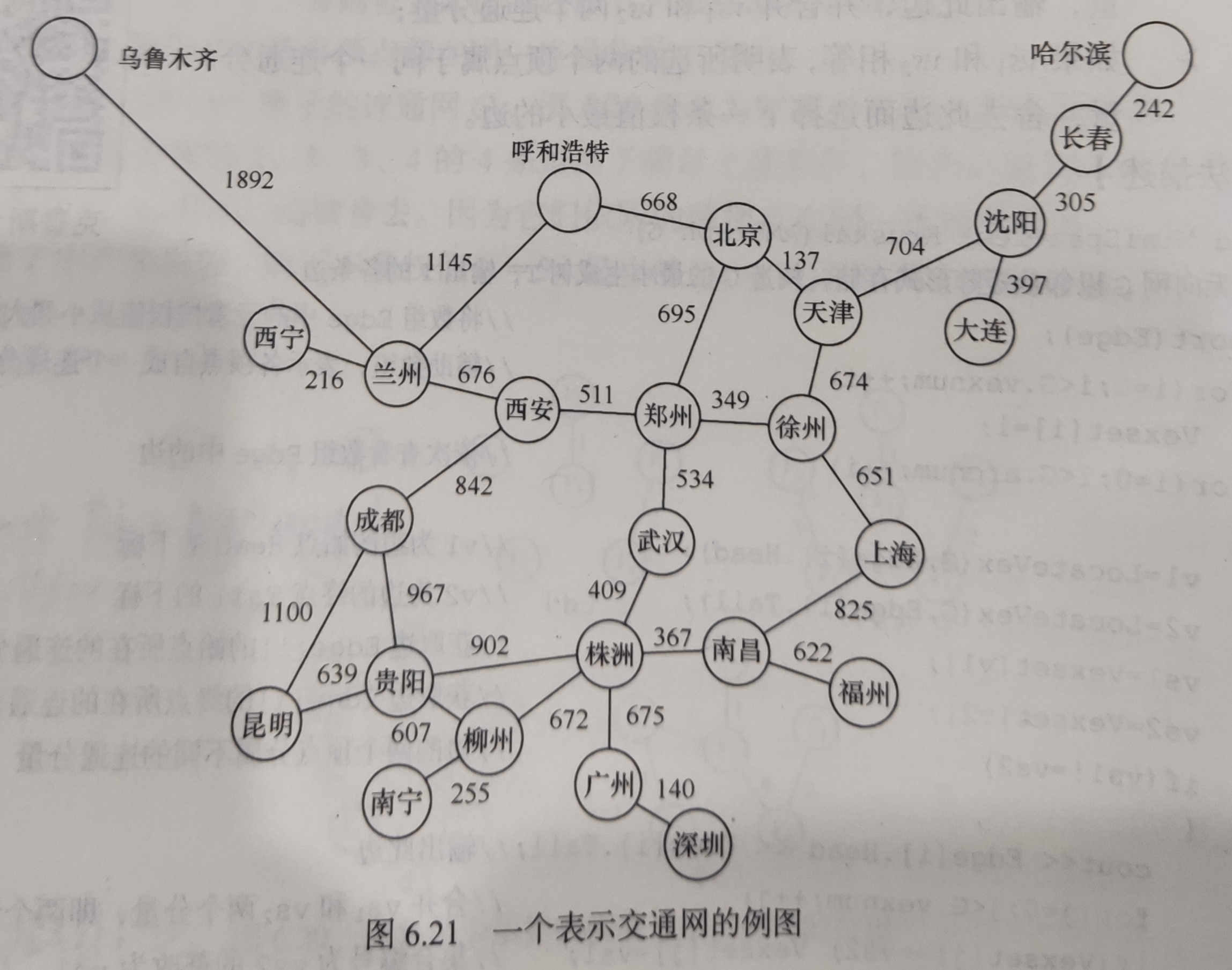
从某个源点到其余各顶点的最短路径（单源最短路）

源点、终点：在带权有向网中，习惯性称路径上的第一个顶点为源点，最后一个顶点为终点。

问题解释：给定带权有向图 G 和源点 v ，求从 v 到 G 中其余各顶点的最短路径。

边权为正数

朴素版Dijkstra $O(n ^ 2)$

算法思想：
对于一个网，算法会将网中的所有顶点分成两组：
第一组：已求出的最短路径的终点的集合（初始时只包含源点v）
第二组：尚未求出的最短路径的顶点的集合

算法将按各顶点与v间最短路径长度递增的次序，逐个将第二组中的顶点加入第一组当中。
在此过程中，总保证从v到第一组中各顶点的路径长度不大于到第二组中各顶点的路径长度

算法实现：
int g[N][N]; // 稠密图用邻接矩阵存
int dist[N]; // 存1号点到N的最短距离
bool st[N]; // 判断点N是否搜索过

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n; i ++ ) 
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j; // t存的是当前还没定好最短距离的点中距离最近的点

        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

堆优化版Dijkstra $O(mlogn)$

struct Edge
{
    int e;
    int w;
    int ne;
} E[N];

int head[110], idx;
int n, m;
int dist[110];
bool vis[110];

void Init()
{
    memset(head, -1, sizeof head);
    idx = 0;
}

void add(int a, int b, int c)
{
    E[idx].e = b, E[idx].w = c, E[idx].ne = head[a], head[a] = idx++;
}

void dijkstra()
{
    memset(vis, false, sizeof vis);
    memset(dist, 0x3f, sizeof dist);
    priority_queue<PII, vector<PII>, greater<PII>> q;
    dist[1] = 0;
    q.push({0, 1});
    while (!q.empty())
    {
        PII temp = q.top();
        q.pop();
        int t = temp.second;
        if (vis[t])
            continue;
        vis[t] = true;
        for (int i = head[t]; i != -1; i = E[i].ne)
        {
            int j = E[i].e;
            if (dist[j] > dist[t] + E[i].w)
            {
                dist[j] = dist[t] + E[i].w;
                q.push({dist[j], j});
            }
        }
    }
}

边权存在负数

Bellman-Ford $O(nm)$

两层for循环，第一层1~n,第二层m条边。
存图方式：傻瓜存图即可，开一个结构体保存每条边的信息。
图中可以存在负环！！！（如果图中存在负环，则最短路径不一定存在）
也可以判断图中是否存在负环，但是时间复杂度很高，不如用spfa判断好。
总结起来"三步走":预处理、松弛操作、三角不等式

struct Edge
{
    int a, b, c;
}edges[M];

int n, m, k;
int dist[N];
int last[N];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < k; i ++ ) // 限制最短路径的最多边数！！！
    {
        memcpy(last, dist, sizeof dist); // 备份，防止出现串联更新问题
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c); // 注意是last[e.a]
        }
    }
}

spfa 一般$O(m)$ 最坏情况$O(nm)$

spfa算法在国际上统称为队列优化的Bellman-Ford算法，只是在中国有这种叫法。
spfa算法使用队列就避免了Bellman-Ford算法中对不需要扩展的节点的冗余扫描。

struct edge
{
    int e;
    int to;
    int val;
} edges[N];

int head[N], idx;
int dist[N];
int n, m;
bool vis[N];

void add(int a, int b, int c)
{
    edges[idx].e = b, edges[idx].val = c, edges[idx].to = head[a], head[a] = idx++;
}

void spfa()
{
    queue<int> q;
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    q.push(1);
    vis[1] = true;
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        vis[t] = false;

        for (int i = head[t]; ~i; i = edges[i].to)
        {
            int j = edges[i].e;
            if (dist[j] > dist[t] + edges[i].val)
            {
                dist[j] = dist[t] + edges[i].val;
                if (!vis[j])
                {
                    q.push(j);
                    vis[j] = true;
                }
            }
        }
    }
}

任意两点之间的最短路径（多源最短路）

问题解释：我们为了求出图中任意两点之间的距离，当然可以把所有点都看成源点，转化为求解n次单源最短路的问题，但是多源最短路的题目往往都是稠密图，且使用Floyd算法可以在O(n^3)内解决问题，它的写法也很简单。

Floyd $O(n^3)$

Floyd算法的思想源于动态规划。其中状态方程为
f[k,i,j]表示“经过若干个编号不超过k的节点”从i到j的最短路的长度。
状态转移方程的思想类似于01背包。
f[k,i,j] = min(f[k-1,i,j], f[k-1,i,k]+f[k-1,k,j])
它的初始状态为f[0,i,j] = g[i,j],也就是我们日常使用的邻接矩阵。
k是阶段，必须置于最外层循环。类似于背包问题的状态压维，k这一维可以省略。
最终我们可以通过三层for使得邻接矩阵g[i,j]表示i到j的最短路的长度。

void floyd()
{
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
memset(g, 0x3f, sizeof g);
for (int i = 1; i <= n; i++)
    g[i][i] = 0;