LCA问题 y总提高课有详细的高阶讲法， 倍增法。简单的暴力方法就是暴搜，然后放到set里，再查第一个在的就是LCA
简单写一下自己的浅显理解
235. Lowest Common Ancestor of a Binary Search Tree
BST对于BST，我们可以根据root点的值和pq的关系决定往哪面走，所以可以进行前序遍历就可以了，因为最多走高度h层，所以时间复杂度时O(h), h 也是logN

236. Lowest Common Ancestor of a Binary Tree
这里首先要明确，在递归函数 dfs遍历tree的时候，他并不会找到LCA就break返回这个LCA的值，而是会遍历整颗树，这也是我开始被绕蒙了的一个地方。一定会递归到root根节点。
找p q的lca，那么对于每一个根节点都要知道子节点的信息：
子节点是否有p， 子节点是否有q，子节点是否已经有lca…
接下来有几种情况
1. 当p，q在root两边的时候，那么root就是p q的LCA
2. 当P或者q就是root的时候，那么就要返回这个点（这里可能会疑惑，那如果root的左子树只有p，那么返回了p，而这个p并不是pq的LCA，要递归到真正的LCA才能找到，所以这块我觉得更严谨的来讲，递归调用本身的lca函数，并不能说是返回lca，返回的意义只是当前这个点子树含有pq的情况，如果都含有那么就说明这个点就是LCA，如果只含有一个就返回那个点，都不含有就返回null）
3. 因为一个root根节点要知道左右子树含有pq的情况，所以采用后续遍历的思路

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;

        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        //后序遍历
        if(root == p || root == q) return root;
        if(left == null) return right;
        if(right == null) return left;
        return root;
    }
}

参考 小呆呆题解 第二种算法 讲的很好

Y总高级解法，设置状态来判断
也是后序遍历，父节点要关注子节点返回的信息， 采用二进制来计数
如果是1，就是有q，如果是二进制10， 也就是2，那就是有p，当state第一次达到3的时候，这个root就是根节点
而且y总的这种写法，可以对子节点找到的情况做判断，如果p或者q不存在，我们也能得到这个信息，在后面的1644题可以用到

class Solution {
    TreeNode ans = null;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root, p, q);
        return ans;
    }

    public int dfs(TreeNode root, TreeNode p, TreeNode q){
        if(root == null) return 0;
        int state = dfs(root.left, p, q);
        state |= dfs(root.right, p, q);

        if(root == p) state |= 2;
        if(root == q) state |= 1;
        if(state == 3 && ans == null){
            ans = root;
        }
        return state;
    }

}

这种写法会有一个疑惑，

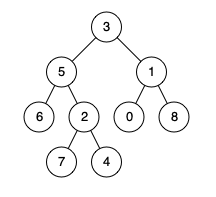
如果找2，4 那么递归到5的时候，也是返回2，递归到3 也是返回2， 递归到1 就会返回 null，
递归到2，会根据2的子节点情况和自己进行比较，如果都是null，就是null，如果left为null就返回right， right为null就返回left，都不为null，就返回该节点

1644. Lowest Common Ancestor of a Binary Tree II
这个题的LCA是当要找的P,Q 可能不存在， 那么在后序遍历的同时，要维护一个是否找到了哪个节点，用y总讲的

class Solution {
    TreeNode ans = null;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        int state = dfs(root, p, q);
        if(state == 3) return ans;
        return null;
    }

    public int dfs(TreeNode root, TreeNode p, TreeNode q){
        if(root == null) return 0;
        int state = dfs(root.left, p, q);
        state |= dfs(root.right, p, q);

        if(root == p) state |= 2;
        if(root == q) state |= 1;
        if(state == 3 && ans == null){
            ans = root;
        }
        return state;
    }
}

1650. Lowest Common Ancestor of a Binary Tree III
有父节点的树，相当于链表找交点的问题，一起往上走，走到头换到另一个node，最终相交的位置就是LCA
循环两倍高度的整棵树，正统做法还是y总讲的像上找，倍增法，暂时还没有理解

y总讲的LCA的第一种做法，暴力解法
从一个点往上走，一直加到root节点进set，然后再将p节点一直往上走，第一个在set里出现的点就是LCA

class Solution {

    Set<Node> set = new HashSet<>();
    public Node lowestCommonAncestor(Node p, Node q) {
        if(p.val == q.val) return p;

        Node x = p;
        while(x != null){
            set.add(x);
            x = x.parent;
        }

        Node y = q;
        while(y != null){
            if(set.contains(y)) return y;
            y = y.parent;
        }
        return x;
    }
}

1676. Lowest Common Ancestor of a Binary Tree IV
采用set计数，像y总讲的解法那样，dfs返回的是那个节点找到了多少个set里的点
后序遍历
236也可以采用这样的做法

class Solution {
    Set<TreeNode> set = new HashSet<>();
    TreeNode ans = null;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {

        for(TreeNode n : nodes) set.add(n);
        dfs(root);
        return ans;
    }

    public int dfs(TreeNode root){
        if(root == null) return 0;

        int left = dfs(root.left);
        int right = dfs(root.right);

        int sumFound = left + right;
        if(set.contains(root)) sumFound++;
        if(sumFound == set.size() && ans == null) ans = root;
        return sumFound;
    }
}