题单:LeetCode Hot 100
1.两数之和
[模拟]
暴力:两重循环,复杂度 $O(n^2)$
哈希表:维护下标
5.最长回文子串
[动态规划] [区间DP]
我们定义 $f[i][j]$ 为 1 时表示 从 $i$ 到 $j$ 是回文串,为 0 时不是。
对于一个子串而言,如果它是回文串,并且长度大于 $2$,那么将它首尾的两个字母去除之后,它仍然是个回文串。
枚举子串长度 len
枚举左端点,此时右端点是确定的
r = l + len -1 ;
if(s[l]==s[r]){
if(len == 2) f[l][r] = true;
else f[l][r] = f[l+1][r-1]
}
else
f[l][r] = false;
上述讨论是针对于子串长度大于 2,所以当子串长度为 2 时需要特殊处理一下
初始 令 $f[i][i] =true$ ;在过程中 ,维护 左端点 和 最大长度
53.最大子数组和
[动态规划] [背包]
我们定义 $f[i]$ 表示 以 $a[i]$ 结尾的最大子数组和
假设我们已知 $f[i-1]$,如何来求解 $f[i]$ 呢
对于第 $i$ 个位置:
- 考虑加入 $f[i-1]$ 的子数组:
f[i-1]+a[i] - 还是另开一段子数组:
a[i]
过程中 维护 一个 $f[i]$ 的最大值即可。
f[i] = max(f[i-1]+a[i] , a[i]) ;
ans = max(ans,f[i]) ;
96.不同的二叉搜索树
[动态规划] [顺序 DP]
考虑第三棵树是如何构建的
第三颗树 一定是由左子树和右子树构成的 (可能为空子树)
-
左子树的结点个数 是从 $0$ 到 $i-1$ , 对应的 右子树的结点 是 $i-1$ 到 $0$
-
结点个数确定之后,下面讨论 整棵树 有多少种
注意这里不要想着一个吃个胖子。
在给的样例中,我们可以得到
g[3] = g[2](3-1) +g[1](3-2)但这 并不是本质规律,只是这个题刚好满足这样的规律
因为
g[2]=f[2]*f[1],g[1]=f[1]*f[1]
令 $f[i]$ 表示 由$ i$ 个结点组成二叉搜索树 的种类数目
由上面的讨论可以得到 $f[i]$ 是由两个 子树构成的,
左子树的种类数目 * 右子树的种类数目 ==》 这种形状 的 二叉搜索树的 种类数目
c++
f[i] = f[j] * f[i-1-j]
Q:为什么确定了 左子树和右子树之后 根节点是确定的呢?
A:这是由于 二叉排序树的中序排列 是严格递增的,左子树和右子树的结点确定之后,只会剩下唯一一个结点 ,即根节点。
312.戳气球
[动态规划] [区间DP]
石子合并 的变种
样例
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
\\ 下面是对样例的解释,k 为戳破的气球,l是左边的气球的下标,r是右边气球的下标,sum 是 f[l][r] 的值
\\ 因为在数组的起始和结尾都插入了一个值为1的结点,所以l最小为0,r最大为5
k=4, l=3,r=5 sum=40
k=3, l=2,r=5 sum=45
k=3, l=2,r=4 sum=40
k=4, l=2,r=5 sum=48
k=2, l=1,r=5 sum=51
k=2, l=1,r=3 sum=15
k=3, l=1,r=5 sum=70
k=2, l=1,r=4 sum=64
k=3, l=1,r=4 sum=135
k=4, l=1,r=5 sum=159
k=1, l=0,r=5 sum=162
k=1, l=0,r=2 sum=3
k=2, l=0,r=5 sum=162
k=1, l=0,r=3 sum=30
k=2, l=0,r=3 sum=30
k=3, l=0,r=5 sum=162
k=1, l=0,r=4 sum=159
k=2, l=0,r=4 sum=159
k=3, l=0,r=4 sum=159
k=4, l=0,r=5 sum=167
思路
我们 定义$ f[l][r]$ 为从 $l$ 到 $r$ 的最大收益,且 $l$ 和 $r$ 不戳破
假设 在 $k$ 处戳破气球受益最大,我们反着思考
没戳破之前 是两堆 “石子” ,分别是 $f[l][k]$ 和 $f[k][r]$
要使得 $l ,k ,r$ 这三个气球能合并的 充分条件是 $l ,k ,r$ 三者相邻
这时题目就转化为 求解在 $f[l][k] $ 中 $l$ 和 $k$ 不戳破且受益最大 和 在 $f[k][r]$ 中 $k$ 和 $r$ 不戳破且收益最大
所以状态转移方程就来啦~
将两堆 “石子” 合并在一块 的受益是 $f[l][k] + f[k][r] + a[l]*a[k]*a[r]$
因为要保证前后都不戳破,我们在数组的起始和结尾加上一个值为 1 的结点
代码
int f[310][310];
class Solution {
public:
int dp(int l,int r,vector<int>& a){
int len = r-l+1;
if(len <= 2) return 0;
if(f[l][r]!=0) return f[l][r];
int res = -1;
for(int k = l+1; k <r; k++){
f[l][r] = max(f[l][r] , dp(l,k,a)+dp(k,r,a)+a[l]*a[r]*a[k]);
}
return f[l][r];
}
int maxCoins(vector<int>& a) {
memset(f,0,sizeof f);
int n = a.size();
a.insert(a.begin(),1);
a.push_back(1);
return dp(0,n+1,a);
}
};
139.单词拆分
class Solution {
public:
bool f[1010];
// 依次检查能否用词典中的单词替代即可
bool wordBreak(string s, vector<string>& a) {
f[0] = true;
int n = s.size(),m = a.size();
for(int i=0;i<n;i++){
if(!f[i]) continue;
for(auto c:a)
if(c.size()+i<=n && c == s.substr(i,c.size()))
f[i+c.size()]=true;
}
return f[n];
}
};
152.乘积最大子数组
[动态规划] [最大子数组]
想要乘积越大,自然是乘的数越多,乘积大的可能性越大。
考虑负数:
- 最大值 是 c 乘 当前连续的最大值 或 c(当前连续的最大值小于 0 )
- 最小值 是 c 乘 当前连续的最小值 或 c(当前连续的最小值大于 0 )
考虑负数:
- 最大值 是 c 乘 当前连续的最小值 或 c(当前连续的最小值大于 0 )
- 最小值 是 c 乘 当前连续的最大值 或 c(当前连续的最大值小于 0 )
考虑 0:
- 最大值 –》0
- 最小值 –》0
class Solution {
public:
int maxProduct(vector<int>& nums) {
int ans = -11 , mx=1,mn=1;
for(auto c:nums){
if(c<0){
swap(mx,mn);
}
mx = max(c,mx*c);
mn = min(c,mn*c);
ans = max(mx,ans);
}
return ans;
}
};
221. 最大正方形
[动态规划]
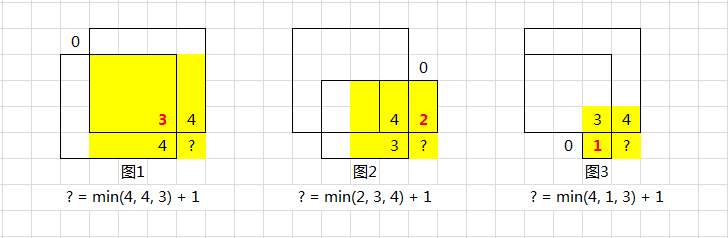
从0到1是很难的这我们都知道,而 DP 是想让你从1 到 2 ,这相对 0 到 2 就简单很多了。
题目中要求正方形的面积,即正方形由多少个格子组成,是一个二维的状态变量,表述起来不方便,我们想办法给他降低一个维度,考虑到 正方形的面积等于边长的平方,故只需要 边长 这个一维标量。
依据 二维差分矩阵 的变量表示方法:用 s[i][j] 以 $(i,j)$ 作为右下角的从 $(1,1)$ 到 $(i,j)$ 的矩阵内所有元素和
此题我们 用 f[i][j] 表示 以 $(i,j)$ 作为右下角的 最大正方形的 边长
考虑 在 $(i,j)$ 一点如何形成最大的正方形
- $(i,j)$ 这点 需要为 ‘1’ (废话)
- 受限制于 上面 $(i-1,j)$,左边 $(i,j-1)$,左上 $(i-1,j-1)$ 三个点
- 三个点彼此限制,但要形成以 $(i,j)$ 为右下的最大正方形,必须取个最小值,再加上 $(i,j)$ 这个点 贡献的 1
下图参考于leetcode题解 偷来的
代码
f[i][j] = min({f[i-1][j-1],f[i-1][j],f[i][j-1]})+1;

