看这个博客之前，强烈建议先把前面的学学再来

考研要点之高级排序的总结:
https://www.acwing.com/blog/content/16486/
考研要点之初级排序的总结:
https://www.acwing.com/file_system/file/content/whole/index/content/4239728/

考研排序（笔试续集）

咱们用了两篇文章的精力终于搞明白初级和高级的排序，但我要说的是那些排序都是基于比较的排序，那么，有没有更焖骚的一些排序呢？耐心看！

前言,精细讲解:

基于比较排序时间复杂度的下界必须要nlogn,因为基于比较的排序,排的序列长度为n的话,那么它的不同的排列的方案数有n!种不同的排列,那么,我们排序的话要保证给予任何数的序列都要将它排成有序,也就是说一个排序算法要想正确的话对于n!种不同的情况,都可以得出正确结果,那么排序过程就是将n!种情况完全分开就可以.

那么,我们假设排序只有两种情况<或>=,也就是说我们划分的时候,每次只能分出来两个分支构建出决策满完全二叉树,那么我们总共要将n!种不同的元素完全分开,也就是说要把每一个集合里的元素数量变成一个点,在叶结点的地方每一次只能包含一个元素,所以说我们在划分的过程中路径的比较次数就是我们的高度,所以这个树的高度下界,就是我们比较次数的下界,整个划分的过程起码要划分成log(n!)次跟nlogn都是同一级别<这里的log都是以2为底>

完蛋,这里竟然有人问我如何证nlogn和log(n!)是同一个级别,行吧,看看我写的图一乐,想深入自己翻书吧

同时,我们也可以将集合划分成不同的判断策略的完全二叉树,每一次往下判断就多一层,也就是log(n!)与nlogn是同一个级别

点到为止,这种深入证明分析,讲多了容易让人干呕，回到正题

桶排序（计数排序）

插个小曲，你要感觉这种理论探讨看不下去，我建议你直接找个书例如《啊哈!算法》直接学生动简单的桶排序，咱们这里就是看了不一定能看懂的去讲，一般考研不会如此刁难人，但要认认真真理解一下的话，学到家还是不错的，真看不懂，直接把代码理解了学会就够了，如果连代码都不理解，直接背下来吧，不丢人！

不基于比较的排序,那就可以做成线性的策略，桶排序就如此。

a0,a1,a2…an-1 1<=ai<=m n->10^5级别
假设我们排序结果是相同元素，相对顺序不发生变化，则结果唯一
ai：取决于小于ai的元素数+等于ai且在ai左边的元素数
举个栗子：
0 1 2 3 4
2 4 1 5 3
比如对于2来说，它在数组里的位置，取决于小于2的数量就1，没有任何元素和2相等，所以说2左边就应该是有1个元素，所以说2的左边的位置应该是1，同理小于4有3个元素，那么排完之后小于4的应该有3个元素在4的左边，那么4就在下标为3的位置，以此类推，我们可以生动形象成如下：
1 2 3 4 5 6 7 … m

我们可以开m个桶，每个桶用来记录这个桶里有多少个元素，
第一个桶里记录值是1的有多少个C1
第二个桶里记录值是2的有多少个C2，
以此类推一直到Cm,
假设我们现在想求小于5的有多少个，相当于C1加到C4，相当于求一个前缀和
所以我们定义一个前缀和Si=C1+C2+…+C
求小于ai的数的个数就是Sai-1
因此，我们预处理Ci数组(O(n))和前缀和Si数组(O(m))都是线性的
这样我就可以确定每个元素最终的位置了，最后把它塞进去即可这部操作还是O(n)

这里不考虑元素相等问题，如果出现的话，规定相等元素相对顺序不发生变化
举栗子：
3 2 x 1 x x 5 x
第一个x应放到所有x的前面所以要小于x的个数：Sx-1
第二个元素应当放到第一个x的后面：Sx-1 + 1
第三个元素应当放到第二个x的后面：Sx-1 + 2
第四个元素应当放到第三个x的后面：Sx-1 + 3 也等于 Sx - 1
所以从后往前排一直到Sx-1为止，至于证明就不展开
模拟个例子：
0 1 2 3 4
3 2 2 1 5
开5个桶：1 2 3 4 5

看看借助前缀和的桶排序写法：

int N = 1000010;//笔试N有多大循环多大，这里的设定是为了一般上机防止数组越界
int q[N], s[N]; //q序列，s前缀和数组
int w[N];       //辅助数组

/*桶排序：如果把上面N（桶的大小）开的更大一点数据会过的更多。但是数值过大
就不太适用*/
void bucket_sort(){
    //统计每个桶里面应该有多少元素，即小于和等于在该元素左边的个数
    for(int i = 0 ;i < n ; i++)   s[q[i]]++;
    //求所有桶的前缀和（循环到数值的最大范围）
    for(int i = 0 ; i < N ; i++)  s[i] += s[i - 1];
    /*把每个元素放到对应的位置上，一定要从后往前放（稳定），先放到
    辅助数组里面，防止产生读写的冲突*/
    for(int i = n - 1 ; i >= 0 ; i --)  w[-- s[q[i]]] = q[i];
    //排完序之后，把序列复制到原数组中去
    for(int i = 0 ; i <  n ; i++)  q[i] = w[i];

}

分析：

①时间复杂度：最好，平均，最坏都是O(n + m)
②空间复杂度：O(n + m)
③稳定！

桶排序看似很快，但数据量一定过大，就撑不住了！这时候，有科学家对此进行优化，引出来了基数排序！

基数排序(桶排序的扩展)

策略（大致讲讲吧，讲的不足评论区见）：

将每个十进制数转化成r进制的
ai -> (d2,d1,d0)r转化成r进制，多关键字
-> 有序数组
基数表示的是进制的基数
在进行排序的时候，每个关键字都在0~r-1之间，很小
——>桶排序即可 O(n+r)
做k次桶排序即可

从高位到地位来做：需要递归用到系统栈
从低位到高位来做，先将所有元素按低位排好序，一次类推用桶排序每一步都来进行多关键字排序，且相对稳定，所以我们有k位，就要进行k次桶排序

每次要做k次桶排序，所以时间复杂度为k(n+r),也可写成d(n+r),这个d表示位数

理论，越讲越无聊，上代码

/*基数排序：d关键字的数量，也就是最多有多少位. r进位制的基数：如2进制，十进制等等*/
void radix_sort( int d , int r){
    //radix进制,从个位开始
    int radix = 1;
    //枚举所有的关键字
    for(int i = 1 ; i <= d ; i ++){
        //清空所有的桶
        for(int j = 0 ; j < r ; j++ ) s[j] = 0 ;
        //统计每个桶里面有多少个元素,q[j] / radix % r:获得对应位上的数，计数
        for(int j = 0 ; j < n ; j++) s[q[j] / radix % r] ++;
        //求前缀和
        for(int j = 1 ; j < r ; j++) s[j] += s[j - 1];
        //按照当前位数上的大小从后往前排序
        for(int j = n -1 ; j >= 0 ;j--) w[--s[q[j] / radix % r]] = q[j];
        //赋值回原数组
        for(int j = 0 ; j < n ; j++) q[j] = w[j];
        //做完当前个位后，往十位、百位上继续，直到最大位数都排完
        radix *= r;
    }
}

基数排序说白了就是做了若干遍桶排序，每一遍都是针对一个关键字，因为桶排序是稳定的，所以基数排序整个过程也都是稳定的

如果你真的不懂基数排序的具体推导，考试出现选择填空之类的题了，你记住，基数排序就是把一组数先按个位上数的大小来排，再按十位上的大小来排，以此类推，就是基数排序的流程，核心在于排序的时候相同数值的相对位置保持不变就行

外排序

区别：基于外存的排序，当我们元素数量很多的时候，就要借助外部空间，在我们内排序的时候瓶颈在于比较次数（移动次数也可以算上），而外排序的瓶颈在于从硬盘上读数据，要求不一样，情景不一样，所以算法也就不一样

策略：

1. 预处理：先利用内存生成一些有序的串m个(m也很大)，每个串都放到一个内存里
2. 归并：将所有m个有序的串归并成一个整个有序串

如果是k路归并，使我们输入k个有序序列进行归并，每次归并k个，类似于二路归并的思想，一共有m路，我们要讲m路归并成一路，每次可以归并k路，那么可以在纸上模拟出来一个归并树，那么每一次都要读一次写一次就是O(logk(m))<注意：这里的log是以k为底>

优化：就是尽可能减少读写次数

1. 置换选择排序（一个算法流程，来生成尽可能长的数据串）
   ①堆排序
   ②败者树（对堆排序的一个优化）
   置换选择排序-说明：拿小根堆举例，在内存里用一个堆来讲输入的元素建立起来，每一次讲堆顶输出到内存缓冲区里面，输出完之后，读入下一个元素且判断是否和刚输出的元素大，大的话就落到堆里面，小于的话就不能放到堆里，要放到刚输出元素的前面，那么此时就应该执行一下堆的删除操作即可，直到堆为空的时候就意味着结束，并开始操作下一个串重复以上步骤

2. 多路归并：
   我们上一步生成的m个数据串不一定相同，每次都要找到最小值，那么我们就可以用一个堆来维护O(log(k)),但是这是个外排序，讨论堆排序中的down(),每次都要比较两次，读两次，而且还有一个致命问题每次输出堆顶的时候都要讲最后一个元素放到堆顶再down()一遍，结束之后还要把新的元素放到堆尾再往上up()走一遍，至少两遍，显得比较慢。。。

   所以我们可以对堆再进行优化，提出胜者树的概念
   胜者树的好处在于可以省去down操作

手绘-自己看吧

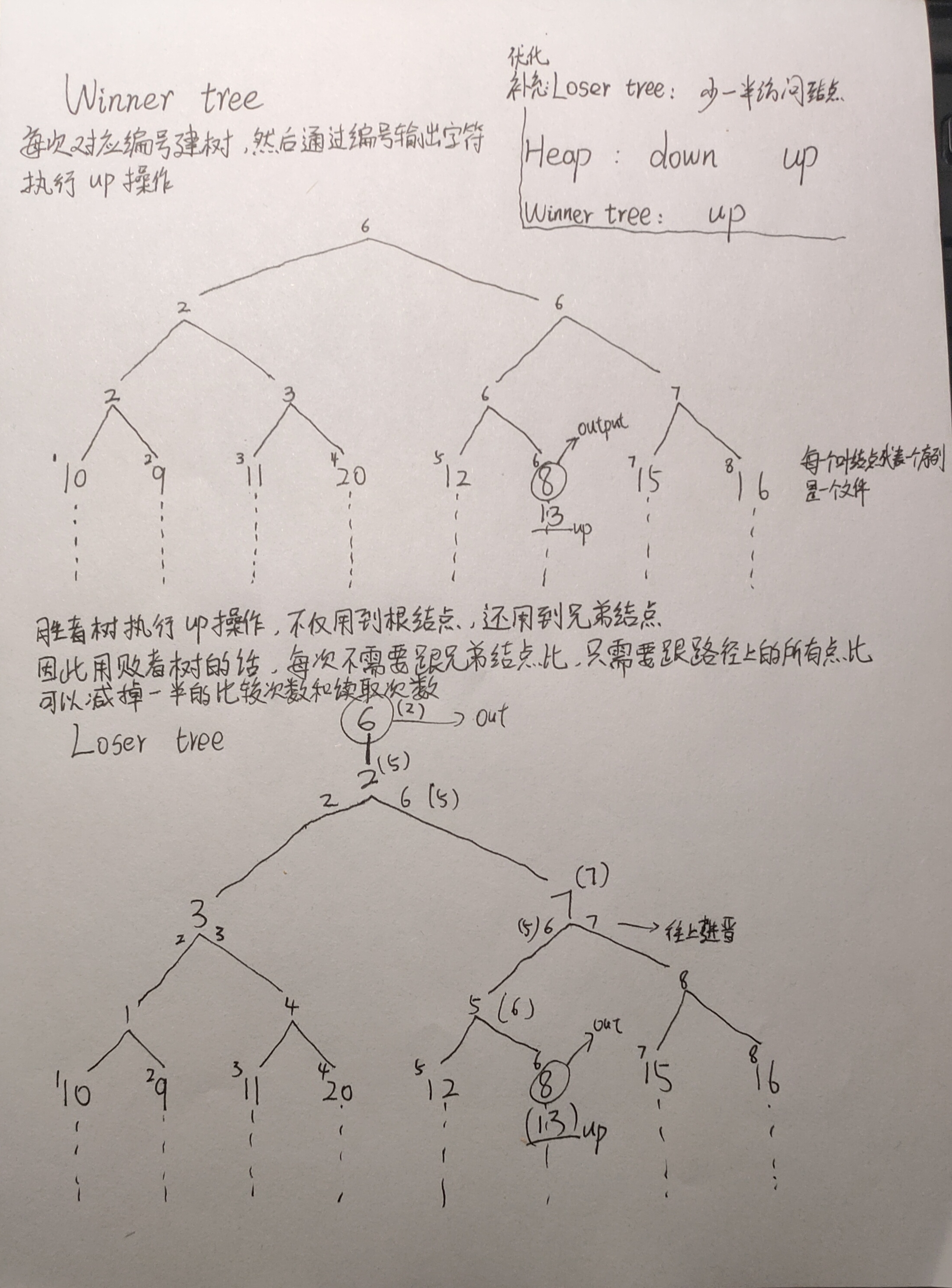
最后要将m段，每次归并k段，长度为k段长度之和，最终归并成一段

归并优化策略：我们每次要选哪k段进行合并，就抽象为典型的哈夫曼树，因此Huffman tree来优化合并过程，我们每次减少k-1段，如果不满足就要补0使得m-1能够被k-1整除，而且这里的零段也称之为虚段

真无语，又说了一堆，简述一下流程：

第一步先用内排序置换选择排序生成最可能长的一些顺段尽可能少的顺段，第二步k路归并，将所有的顺段都归并成一路，在归并的过程用Huffman tree来优化(每次挑长度最小的顺段)进行归并且归并的时候我们要用败者树来实现

注意：外部排序尽可能优化常数来调整效率节省时间，说白了还是数据量太长了，不优化很有可能跑一天，所谓优化常数说白了就是对时间复杂度前面的系数进行优化调整

总结：
所有的 内部排序一般都是宜采用顺序存储比较好
大根堆元素调整的时候比较次数，比较失败的也算一次。
每趟排序至少能确定一个元素的最终位置的排序有：简单选择排序、快速排序
（考研教材上的可以确定，但是y总的代码不能保证，以考研为准）、堆排序（堆排的
一趟指的是每次将最小或最大的放在堆顶）、
折半插入排序比直接插入排序优化的是比较次数
基数排序如果没有说明就是按照十进制来排，
判断希尔排序的增量，我们可以不用模拟整个过程。
把每个选项的增量带入题中看哪1个是升序哪1个降序（看这一小段的），
就可以推出这个希尔的增量是多少。因为正确答案唯一，其余三个肯定会跟正确答案逆序。
快速排序的第 i 趟的序列，判断依据： 至少有 i 个元素会出现在正确的位置上
（判断一个元素是不是在最终位置上，可以看左边的元素是不是都比他小右边的都比他大，不用）。
希尔排序和堆排序采用链式存储效率会变低，因为他们要用到随机索引。
（堆排序排序时采用数组模拟的，不是那种树结构的）

先说这么多吧！有意见，发现问题，咱们评论区见！