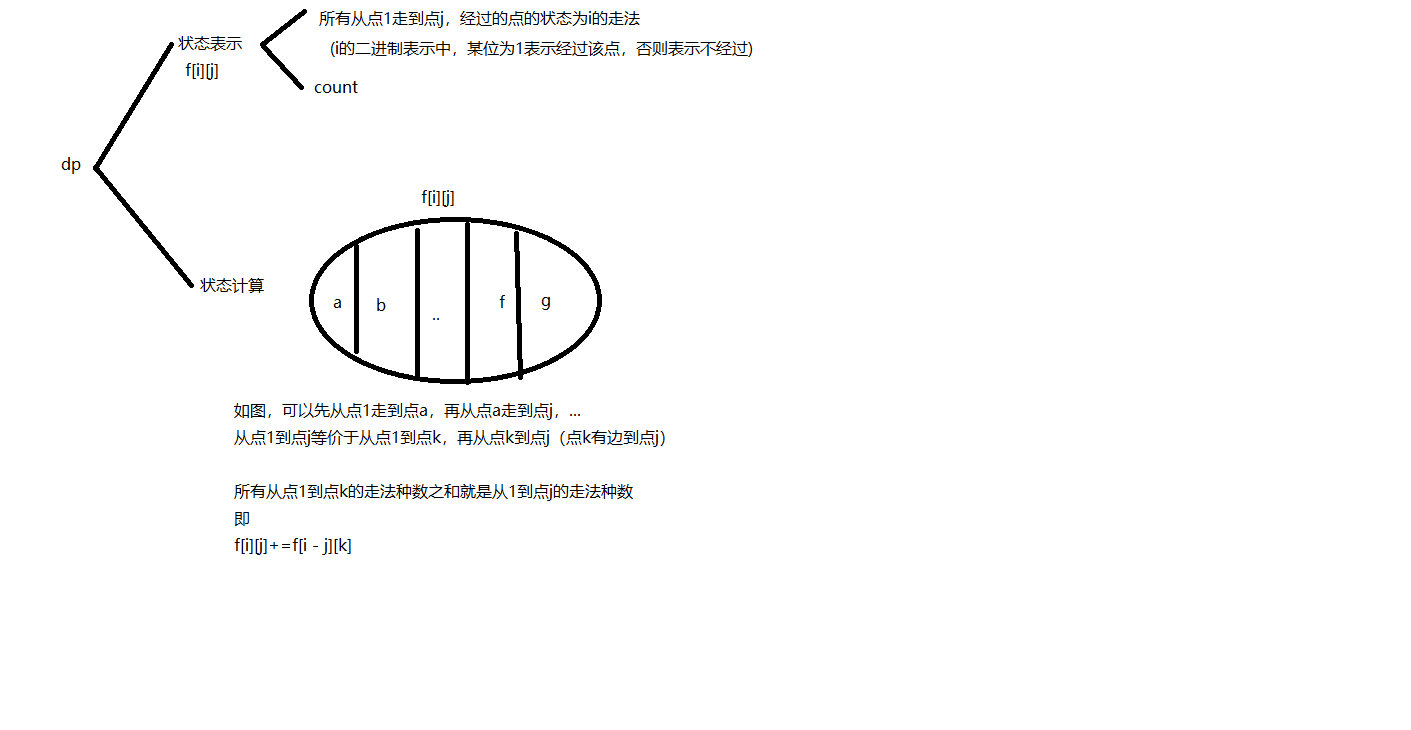
跟最短哈密顿回路一样，用二进制状态压缩

class MC{

    int N = 1 << 21, M = 21;
    long f[][] = new long[N][M];
    boolean w[][] = new boolean[M][M];

    int gcd(int a, int b) {
        return b > 0 ? gcd(b, a % b) : a;
    }

    public void run(){
        for(int i = 1; i <= 21; i++) {
            for(int j = 1; j <= 21; j++) {
                if(gcd(i, j) == 1) {
                    w[i - 1][j - 1] = w[j - 1][i - 1] = true;
                }
            }
        }

        //没经过点，到达点1，初始状态
        f[1][0] = 1;
        for (int i = 1; i < N; i++) {
            for (int j = 0; j < M; j++) {
                //走到点j，当前状态必须包含点j
                if(((i >> j) & 1) == 0) continue;
                //查找从k到j的点
                for (int k = 0; k < M; k++) {
                    //当前状态不经过点j的时候，经过了点k且有k到j
                    if (((i ^ (1 << j)) >> k & 1) == 1 && w[k][j]){
                        f[i][j] += f[i ^ (1 << j)][k];
                    }
                }
            }
        }
        long res = 0;
        //所有从点1走到点i，经过的状态为21个1的种数
        for(int i = 0; i < 21; i++) {
            res += f[(1 << 21) - 1][i];
        }
        System.out.println(res);
    }

}

public class Main {
    public static void main(String[] args) {
        new MC().run();
    }
}