差分约束习题精讲
图论讲解
1.差分约束的相关概念
$\space\space\space\space\space$差分约束本质上就是一种新的“最短路”的模型 所以我们可以用最短路等图论知识求解
$\space\space\space\space\space$差分约束系统是一种特殊的N元一次不等式组 它包含N个变量 $X_1$ ~ $ X_N$ >以及M个约数条件 每个约束条件都是由两个变量作差构成的 形如$X_i - X_j \leq C_k$ 其中$C_k $ >为常数(可以是非负数 也可以是负数) 1 $\leq$ i, j $\leq$ N, 1 $\leq$ k $\leq$ M, 我们要解决的问题就是 >求一组解$X_1 = a_1 X_2 = a_2 ..... X_n = a_n$ 使所有约数条件均可以满足
$\space\space\space\space\space$通俗一点地说,差分约束系统就是一些不等式的组,而我们的目标是通过给定的约束>>不等式组求出最大值或者最小值或者差分约束系统是否有解。
$\space\space\space\space\space$差分约束系统的每个约数条件 $X_i - X_j \leq C_k$ 可以变形为$X_i \leq X_j + >C_k$ 这与单源最短路问题中的三角不等式 dist[y] $\leq $ dist[x] + z非常相似 因此可以把每个变量$X_i$看作有向图中的一个节点i 对于每个约数条件 $X_i - X_j \leq C_k$ >从节点j向节点i连接一条长度为$C_k$的有向边
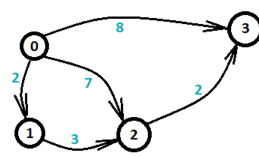
$\space\space\space\space\space$例如
$\space\space\space\space\space$ $n = 4$
$\space\space\space\space\space$ $x_1 - x_0 \leq 2 ①$
$\space\space\space\space\space$ $x_2 - x_0 \leq 7 ③$
$\space\space\space\space\space$ $x_3 - x_0 \leq 8 ②$
$\space\space\space\space\space$ $x_2 - x_1 \leq 3 ④$
$\space\space\space\space\space$ $x_3 - x_2 \leq 2 ③$
$\space\space\space\space\space$然后经过计算就变成了如下
1、③ $\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space$ $x_3 - x_0 \leq 8$
2、②+⑤ $\space\space\space\space\space\space\space\space\space\space$ $x_3 - x_0 \leq 9$
3、①+④+⑤ $\space\space\space\space\space$ $x_3 - x_0 \leq 7$
$\space\space\space\space\space$对于每个不等式 $X_i - X_j \leq C_k$对结点 j 和 i 建立一条 j−>i的有向边,边权为$C_k$,求$X_{n - 1} -> X_0$ 的最大值就是求 0 到n−1的最短路。
2.差分约束的求解
2.1 从数形结合上看
从数形结合上看的定义如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵
中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。
$\space\space\space\space\space$ $x_1 - x_0 \leq 2 ①$
$\space\space\space\space\space$ $x_2 - x_0 \leq 7 ③$
$\space\space\space\space\space$ $x_3 - x_0 \leq 8 ②$
$\space\space\space\space\space$ $x_2 - x_1 \leq 3 ④$
$\space\space\space\space\space$ $x_3 - x_2 \leq 2 ③$
然后转化为邻接矩阵则表示为
2.2 从三角不等式上看
B−A$\leq$c①
C−B$\leq$a②
C−A$\leq$b③
$\space\space\space\space\space$我们从三角不等式转化为图论图形
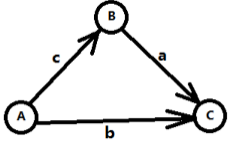
$\space\space\space\space\space$ 我们要想知道C - A的最大值 通过 ① + ② 可以得到$C - A \leq a + c$ 所以这个问题其实就是求 min(b, a + c)
$\space\space\space\space\space$ 三角不等式可以推广到m个 变量推广到n个 就变成了n个点m个边的最短路问题
3 差分约束的应用
$\space\space\space\space\space$差分约数系统的应用很光 都会有一定的背景 我们只需要根据题意构造出差分约束系统 然后在根据题目的要求求解就行
$\space\space\space\space\space$一般题目会有三种情况 (1)判断差分约束系统是否有解 (2)求取最大值 (3)求取最小值
1.判断差分约束系统是否有解
$\space\space\space\space\space$我们知道最短路问题 会出现负环或者根本不可达到的情况 所以我们的差分约束也有类似情况
$\space\space\space\space\space$ 差分约束的解有三种情况
1.有解
2.无解
3.无限多解
1.1 无解
$\space\space\space\space\space$如果路径出现负环 就代表最短路可以无限小 即不存在最短路 那么在不等式上的表现就是在形如$X_i - X_{i - 1} <= K$该式子中的K无限小 那么得出的结论就是$X_i - X_{i- 1}$的最大值不存在 即 if(cnt[j] >= n + 1) return false;
ps 在判断是否存在环的情况时 我们对于怎样建图都无太大问题 所以我们可以直接建最大值 即最短路模型判断负环
1.3 无限多解
$\space\space\space\space\space$这种情况表明$X_i 和X_{i - 1} $ 之间没有约束关系 $X_i - X_{i - 1}$的最大值无限大 即$X_i 和X_{i-1}$的取值有无限多种 在代码中表示为dist[n] = INF;
2.1 求取最大值
$\space\space\space\space\space$求取最大值 即取最短路 例如
$\space\space\space\space\space$ 对形如$X_i - X-{i - 1} \leq A_k$的不等式 求$X_3 - X_0 $的最大值
$\space\space\space\space\space$ $x_1 - x_0 \leq a ①$
$\space\space\space\space\space$ $x_2 - x_0 \leq b ③$
$\space\space\space\space\space$ $x_2 - x_1 \leq c ②$
我们进行画图 如下
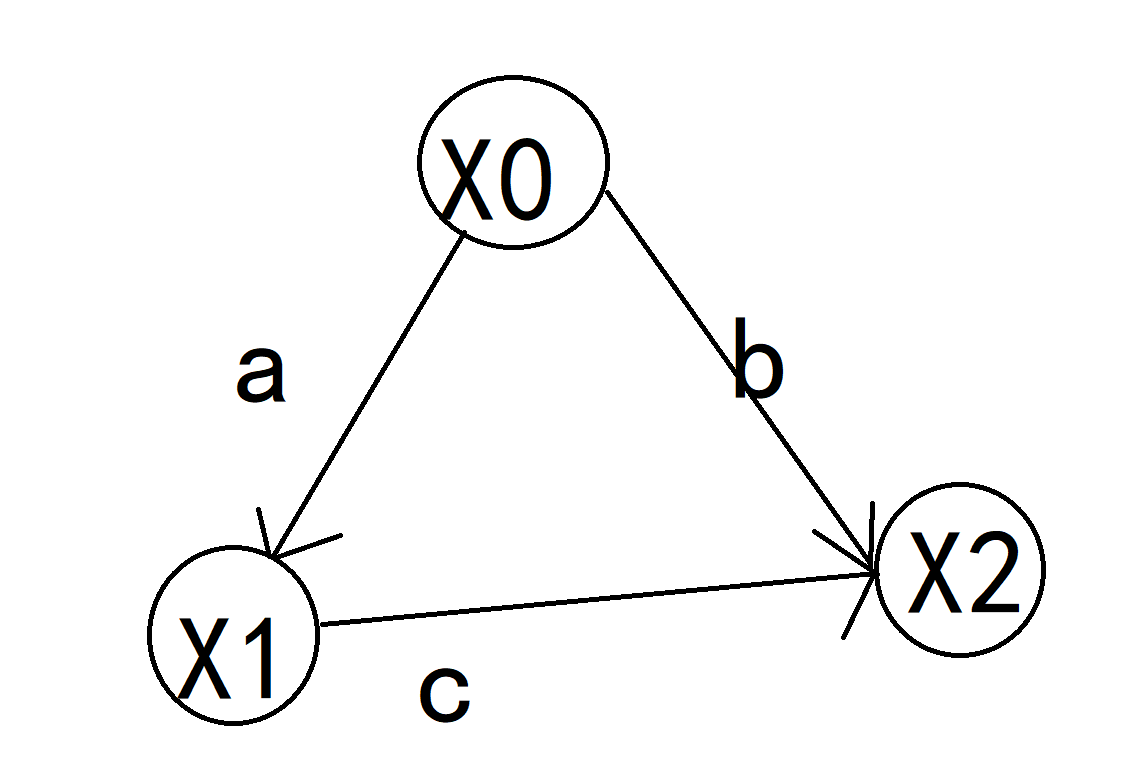
$\space\space\space\space\space$ 要是等式①③②取最大值 即求 从$X_0 -> X_2$的最小值(小于等于取满足的最大值 显然即所有不等式解的区间最小值)换言之 即求min(a, b + c)即最短路
2.2 求取最小值
$\space\space\space\space\space$求取最小值 即求最长路
$\space\space\space\space\space$观察问2 只需要将符号进行改变 转化成最长路问题判断即可
ps 除了判断存在问题 题目给定求最长路不要转化成最短路问题 在 种树转化出现问题
4.差分约束的实现方式
$\space\space\space\space\space$由前文可知 我们是将不等式所建成了一个图 而以$A - B \leq C$的形式 我们转化为最短路模型 而$A - B \geq C$则转化为最长路模型 众所知周 spfa在进行求解最长路最短路的时候优势极其大 因为通常而言 唯一能判断负环存在的仅仅只有spfa 但是最特殊情况下 我们将其转化的是最短路模型 在符合其他最短路应用条件的时候 也可以用其他最短路算法实现 比如在多源情况下的floyd 例题 天平就是基于floyd写法的差分约束 在比如 我们的拓扑排序在DAG图中也能求出最长路 所以我们也可以用拓扑排序解决某类差分约束问题 差分约束 是一种图论最短路的模型 而不仅仅是spfa的一种应用
5.差分约束的求解过程

ps 对于上述是给定边的差分约束 如果是基于点的差分约束问题 即给定A B求A和B之间的判断(包括AB)等 我们可以用前缀和 转化成sum[B] - sum[A- 1]的差分约束系统 如种树
ps-2 在常规的判断中 我们需要考虑所有子图是否全部连通的情况 而对于某些问题是问到 某些子图可能并不连通的情况 所以我们可以建立一个虚拟原点 进而将所有子图进行虚拟连通 进而容易判断 需要注意的是 针对点的差分约束情况 我们的虚拟原点不能为0因为 sum[A-1]是包含0这种情况的 所以在点的差分约束系统中 我们默认的虚拟原点应该为 n + 1
6.差分约束的转化思路

6.实际例题分析
1.差分约束模板题
2.小k的农场 边的差分约束判断题
3.狡猾的商人 点的差分约束判断问题
4.糖果 边的差分约束最值问题
5.工程规划 边的差分约束输出问题
6.种树点的差分约束输出问题
7.区间取数多组点差分输出问题
8.天平 基于floyd写法的差分约束

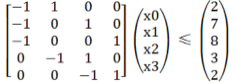

谢谢,爱你摸摸哒mua~
巨巨 mumuda