A. Madoka and Math Dad

解题思路

根据样例发现总是“2121···”或“121212”
为什么是这样呢？因为1和2是最小的两位数，通过这样的交替，我们可以使得分解出的位数更多
通过模拟一些例子我们可以发现其实就是对%3做讨论:
如果n % 3 == 0, 则输出(n / 3) 个 “21” (比“12”更大)
如果n % 3 == 1, 则输出(n / 3) 个 “12” (拆解出的位数更多) + 末尾的一个”1”
如果n % 3 == 2, 则输出(n / 3)个 “21” (比“12”更大) + 末尾的一个”2”

Code

void solve()
{
    int n; cin >> n;
    if(n % 3 == 1)
    {
        for(int i =1;i <= n / 3; i++) cout << "12";
        cout << 1 << '\n';
        return;
    }
    if(n % 3 == 2)
    {
        for(int i = 1; i <= n / 3; i++) cout << "21";
        cout << 2 << '\n';
        return;
    }
    for(int i = 1;i <= n / 3; i++) cout << "21";
    cout<<'\n';
}

B. Madoka and the Elegant Gift

题目大意

对于一个01矩阵，询问其中是否有两个极大的仅由 “1” 组成的子矩阵
通俗点来说：如果有一个连通块不为矩形，则输出“NO”， 否则输出“YES”;

解题思路

问题的关键在于我们如何判断一个连通块是否是矩形
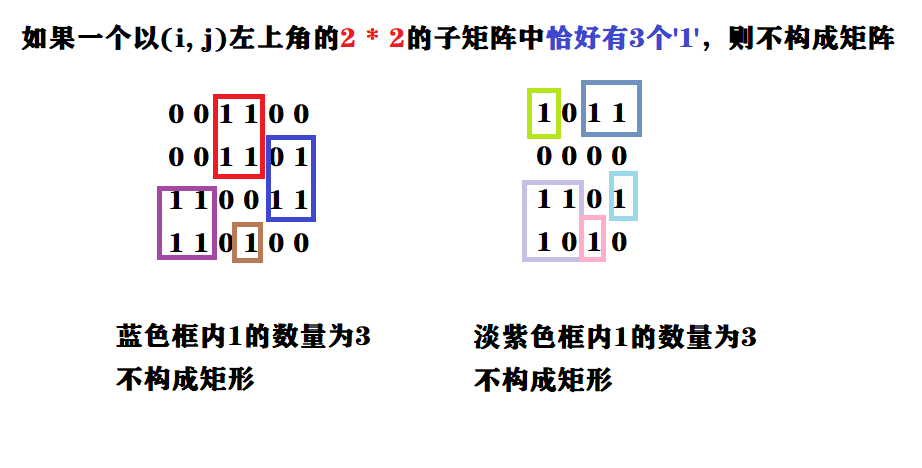
一个判断是否为矩阵的方法:如果一个以$(i, j)$左上角的$2 * 2$的子矩阵中恰好有3个‘1’，则不构成矩阵

Code

void solve()
{
    int n, m;   cin >> n >> m;
    for (int i = 1; i <= n; i++)    
        for(int j = 1; j <= m; j++) 
            cin >> g[i][j];

    for (int i = 1; i < n; i++)
        for (int j = 1; j < m; j++)
            if (g[i][j] - '0' + g[i + 1][j] - '0' + g[i][j + 1] - '0' + g[i + 1][j + 1] - '0' == 3)
            {
                puts("NO");
                return;
            }

    puts("YES");
}

C. Madoka and Childish Pranks

题目大意

初始01矩阵‘G’的格子均为0，你可以进行若干以下操作，需要使得矩阵变为目标矩阵$A$。
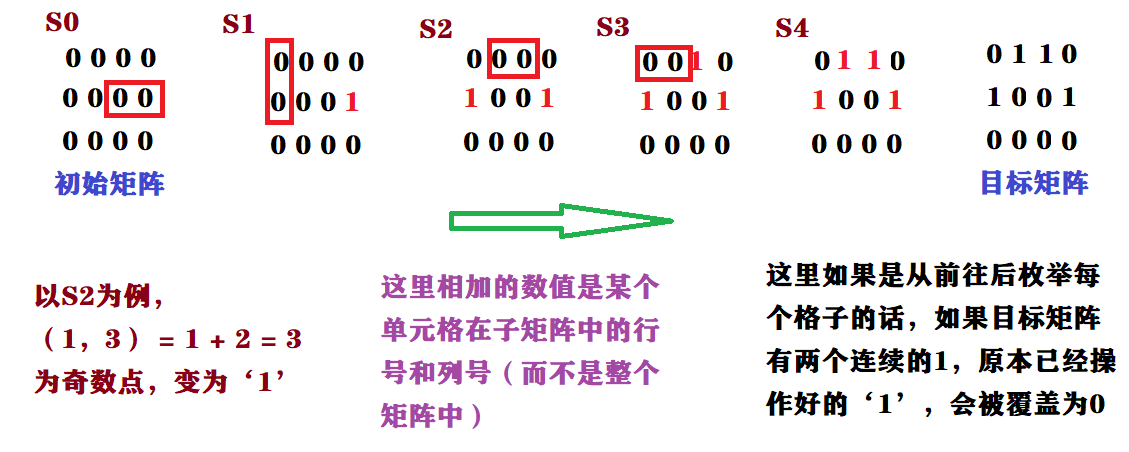
选定矩阵的一个子矩阵 $B$ ，将 $B$ 中，偶数点（元素在B中的行号加列号为偶数，例如B中的第一行第一列）赋值为0，奇数点赋值为1。

解题思路

本题有一种特殊情况:
目标矩阵中，第1行第1列需要为 0 (若为1，任何操作都无法将其变为这个元素变为1, 因为第1行第1列在任何子矩阵中都为偶元素)
排除这种特殊情况之后，我们可以发现任意给定的目标矩阵都可以通过初始矩阵得到
比如在j >= 2的情况下, 任意G[i][j]这个点我们可以通过以G[i][j - 1]为左侧的$1 * 2$子矩阵来使得它变为‘1’;
特殊地，如果j = 1的情况下，任意G[i][1]这个点我们可以通过以G[i - 1][1]为上侧的$2 * 1$子矩阵来使得它变为‘1’;

不过我们这里需要从后往前枚举每个单元格

因为如果是从前往后枚举每个格子的话，如果目标矩阵有两个连续的1，原本已经操作好的‘1’，会被覆盖为‘0’

Code

struct node {
    int a, b, c, d;
};
char b[N][N];

void solve()
{
    int n, m;   cin >> n >> m;
    vector<node> res;

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> b[i][j];

    if (b[1][1] == '1') {puts("-1"); return;}  // 特殊

    for (int i = n; i >= 1; i--)
        for (int j = m; j >= 1; j--)  // 从后往前枚举，以免操作覆盖
        {
            if (b[i][j] == '0') continue;
            if (j == 1) res.push_back({i - 1, j, i , j});  // j = 1的情况
            else res.push_back({i, j - 1, i, j});
        }

    cout << res.size() << endl;
    for (auto x : res)  cout << x.a << ' ' << x.b << ' ' << x.c << ' ' << x.d << endl;
}

D. Madoka and the Best School in Russia (动态规划)

题目大意

给定两个数字 $x, d(x, d \le 10^9)$ ，问能否将 $x$ 用至少两种方式拆成 $x=x_1 * x_2 * x_3····$ 。
其中 $x_i$ 是 $d$ 的倍数，但不是 $d^2$ 的倍数。

解题思路

看了看官方题解，本题可以用动态规划的方式来做
我的理解是将n倒着来处理，也就是从n变1
开一个dp[a][b] = c 的二维数组，表示a上一次被b除后，所得的方案数为c
对于每一个状态，我们枚举满足条件的数 $i$ ，看看能否整除 $a$ ，且大于等于 $b$
由此可得状态转移方程$dp[n / i, i] = dp[n / i, i] + c$

这里为什么要大于等于b呢？=> 这样做可以满足除数递增，是为了防止重复计数

早上看到了 @Snow_rawdl的做法觉得很不错，感兴趣点击这里
下面代码为动态规划做法

Code

int x, d;
bool check(int n)  // 检查是否符合条件
{
    if (n % d == 0 && n % (d * d) != 0) return true;
    return false;
}

void solve()
{
    cin >> x >> d;
    vector<int> del;    map<PII, int> dp;
    dp[{x, 1}] = 1;  // 初始化

    for (int i = 1; i * i <= x; i++)  // 将满足条件的因子存起来
        if (x % i == 0)
        {
            if (check(i))   del.push_back(i);
            if (x != i * i && check(x / i)) del.push_back(x / i);
        }

    int res = 0;  // 记录a == 1时的方案数
    while (dp.size())
    {
        auto now = *dp.rbegin();  // 倒序，从n往1走
        int a = now.first.first, b = now.first.second, c = now.second;
        if (a == 1) res += c;

        for (auto i : del)  // 枚举每个满足条件的数
            if (a % i == 0 && i >= b)   dp[{a / i, i}] += c; // i >= b是为了避免重复加
        dp.erase(now.first);  // 处理完后删除尾部
    }

    if (res > 1)    puts("YES");
    else puts("NO");
}

PS: 本人代码头文件中带有”define int long long”，
如出现wa可能是精度问题， 使用需将”int main()” 改为”signed main()”