历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

动态规划个人总结

作者：

DueGin , 2022-03-10 09:53:32 , 所有人可见 , 阅读 569

8

13

动态规划

以下为自己的理解及结合各种题解得出的总结

DP分析：

状态表示$f(i,j)$ （从集合的角度考虑dp问题）（先确定是几维）
- 集合表示的是什么
  - 所有选法
  - 满足条件
    - 只从前 $i$ 个物品中选
    - 总体积小于等于 $j$
- 表示的属性是什么（一般是Max，Min，数量 …）
状态计算
- 集合的划分
DP优化：
- 对状态方程等价变形

j和j-v[i]都是小于等于j的，他们都是在同一侧，而不是在两侧，好办

时间复杂度，状态的数量 * 转移的计算量

背包问题模型

需要确定以下概念分别是什么：

背包容量
物品体积
（物品价值）

背包问题解题套路：

遍历物品
- 遍历体积
  - (遍历）决策

而分组背包稍有特殊：

遍历物品组
- 遍历体积
  - 遍历组内物品（遍历决策（状态转移））

通用的三种状态初始化：

体积不超过 $j$，初始化全部为 $0$，$v ≥ 0$
体积恰好为 $j$，初始化 $f[0] = 0$，其余为 $+/- ∞$，$v ≥ 0$
体积至少为 $j$，初始化 $f[0] = 0$，其余为 $+/-∞$，（$v$ 可以为负数，且 $v$ 为负数时，相当于什么都不选，即从 $f[0]$ 转移过来）

01背包

01背包 DP分析：

01背包分析

需要注意的是：这里的上一个状态是当前状态我是要选第 $i$ 件物品的，但我先不选，就有了不选 $i$ 的最优子结构，然后加上选了之后，那也还是最优子结构

$f(i, j)$ 是从前 $i$ 个物品选，且总体积不超过 $j$ 的权重的最大值

特点：每件物品最多只选一次

基础题：AcWing 2. 01背包问题

for(int i = 1; i <= n; i++) // 遍历每一种状态(遍历考虑前i件物品 选 or 不选)
    for(int j = 0; j <= m; j++) //遍历背包容量 
    {
        f[i][j] = f[i - 1][j]; // 本次状态 不选物品 必然可以发生
        if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); // 而选第i件物品需要满足背包能装得下
    }

第一种优化：因为每次都只用到上一层的数据，只需开两个一维数组来回滚动即可

int f[2][N];
for(int i = 1; i <= n; i++) // 遍历每一种状态(遍历考虑前i件物品 选 or 不选)
    for(int j = 0; j <= m; j++) //遍历背包容量 
    {
        f[i & 1][j] = f[(i - 1) & 1][j];
        if(j >= v[i]) f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - v[i]] + w[i]);
    }

第二种优化：因为每次都只用到上一层的数据，而且 $j - v[i]$ 都是小于 $j$ 的，他们都是在同一侧，而不是在两侧，好办，所以可以将 $f(i, j)$ 优化成一维。需要注意的是遍历的顺序有所改变

以本题为例：

我们在删除一维的时候，由于在选不选第 $i$ 件物品需要用到上一层的数据，所以为了防止在修改数据时，把上一层前面的数据都修改了，只好从后往前遍历

即：

for(int i = 1; i <= n; i++) // 遍历每一种状态(遍历考虑前i件物品 选 or 不选)
    for(int j = m; j >= v[i]; j--) //遍历背包容量 
        f[j] = max(f[j], f[j - v[i]] + w[i]);

实在不懂去看y总视频吧，空降 ⌈动态规划(一) ⌋ 40: 41

可以发现：01背包优化掉一维后，枚举体积都是从大到小枚举的

01背包裸题：

NOIP 2005 普及组：AcWing 423. 采药
《信息学奥赛一本通》：AcWing 1024. 装箱问题
NOIP2006普及组：AcWing 426. 开心的金明

Google Kickstart 2019：AcWing 734. 能量石贪心 + DP，需要利用贪心的性质先排个序，难在贪心，具体看打卡详解

完全背包

DP分析：

完全背包分析

特点：相对于01背包问题，完全背包的物品可以选无限个

基础题：AcWing 3. 完全背包问题

优化：

$f(i, j) = max(f(i-1, j), f(i-1, j-v)+w, f(i-1, j-2v)+2w, …)$

$f(i , j - v) = max(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f(i-1, j-v),\ \ \ \ \ \ \ \ f(i-1, j-2v)+w,f(i-1, j-3v)+2w, …)$

可以看出上面两式后面非常相似，即：$f(i, j) = max(f(i - 1,\ j),\ f(i,\ j - v) + w)$

优化到此处，还可以继续优化，这个结构与01背包很像，所以套用01背包的优化即可，即优化成一维，但注意的是，这里用的是本层的 $i$ ，所以在遍历 $j$ 的时候需要从前往后遍历

AcWing 900. 整数划分也是计数DP

多重背包

DP分析：

多重背包分析

特点：物品只能选有限个

多重背包Ⅰ$O(n\cdot m\cdot s)$ $n$ 是物品种数，$m$ 是背包体积，$s$ 是物品个数

基础题：AcWing 4. 多重背包问题

优化：（二进制优化）

$O(n\cdot m\cdot log\ s)$

基础题：AcWing 5. 多重背包问题 II

尝试使用完全背包同样的优化方法：

$f(i, j) = max(f(i-1, j), f(i-1, j-v)+w, f(i-1, j-2v)+2w, … \ ,f(i - 1,j-sv)+sw)$

$f(i , j - v) = max(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f(i-1, j-v),\ \ \ \ \ \ \ \ f(i-1, j-2v)+w, …,\ \ \ f(i-1,j-sv)+(s-1)w,\ f(i-1,j-(s+1)v)+sw)$

显然，多出来一项，直观认为拿他没办法

所以寻求一种更加牛逼的方法：二进制优化

二进制优化：

我们知道 $2^k$ 在二进制数中第 $k+1$ 位上是 1，其余全是0 ，那么从 1~$2^k$ 中选择其中若干个数来求和，能得到 $[1,2^{k+1}]$ 中的所有数

则可以用这种方法将我们遍历的个数缩小到 $log_2s$ 个

而 1~$2^k$ 中所有数求和 ==> $2^{k+1}-1$

例1：s为1023

1，2，4，8，… ，2^k^ ，2^k+1^

1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 =1023

即：a = 1，2，4，8，16，32，64，128，256，512

如果 $2^{k+1}-1>s$ ，则 $2^k$ 不能要，因为1~$2^k$任选所有数相加可以表示$[1,2^{k+1}-1]$的数，所以此范围表示的数超过了 s ，则不可取

例2：s 为200

1，2，4，8，16，32，64，128 ==> 全部加起来等于255

所以128不能要，

而1~64 只能覆盖 $[1,127]$ 则剩下的这个数即是：$s - 127 = 73$

即：a = 1，2，4，8，16，32，64，93

了解了二进制优化后，我们可以将其按照形如 $a$ 数量序列打包，打包后即可发现新大陆，每个包最多只选一次，这就转化为了01背包问题，于是二进制优化后，再做一次01背包即可

进一步优化

利用单调队列进行优化

$O(n \cdot v)$ $v$ 是背包体积 mod 每种物品的体积的模数

多重背包原始状态转移方程：
$$ f(i,j)=max(f(i−1,j),f(i−1,j−v)+w,⋯,f(i−1,j−sv)+sw) $$
尝试用完全背包的优化方式来优化此方程：
$$ f(i,j−v)=max(f(i−1,j−v),f(i−1,j−2v)+w,⋯,f(i−1,j−(s+1)v)+sw) $$
发现多了一项 $f(i - 1, j - (s + 1)v + sw)$，由于多重背包的每件物品的数量是有限的，不能像完全背包优化那样能整体替换，但我们继续往下推导公式：
$$ \begin{cases} f(i,j)=\ \ \ \ \ \ \ \ \ max(f(i−1,j),\ \ \ \ \ \ \ \ \ f(i−1,j−v)+w,⋯,\ \ f(i−1,j−sv)+sw) \\\\ f(i,j−v)=\ \ max(f(i−1,j−v),\ \ f(i−1,j−2v)+w,⋯,f(i−1,j−(s+1)v)+sw) \\\\ f(i,j−2v)=max(f(i−1,j−2v),f(i−1,j−3v)+w,⋯,f(i−1,j−(s+2)v)+sw) \\\\ f(i,j−3v)=max(f(i−1,j−3v),f(i−1,j−4v)+w,⋯,f(i−1,j−(s+3)v)+sw) \\\\ f(i,j−4v)=max(f(i−1,j−4v),f(i−1,j−5v)+w,⋯,f(i−1,j−(s+4)v)+sw) \\\\ ⋯ \\\\ \end{cases} $$
还看不出来的话，不妨将 $f$ 数组优化掉一维，即表示容量为 $j$ 的情况下，获得的最大价值

可以更新一下 $f[m]$ —> $f[0]$ 的值，最后$f[m]$ 即为全局最优值
$$ f[m]=max(f[m],\ f[m - v] + w,\ f[m - 2\cdot v] + 2\cdot w,\ …\ , f[m - k\cdot v] + k\cdot w) $$
上述式子是从后往前推的，我们不妨从前往后推 $f[0]$ —> $f[m]$ ，即在 $j$ 体积的前提下选 $k$ 件物品 $i$ 的最大价值，并将其枚举开来：
$$ \begin{cases} f[0],\ f[v],\ \ \ \ \ \ \ \ f[2\cdot v],\ \ \ \ \ \ \ \ f[3\cdot v],\ \ \ \ \ \ \ \ …\ ,\ f[k\cdot v]\\\\ f[1],\ f[v + 1],\ f[2\cdot v + 1],\ f[3\cdot v + 1],\ …\ ,\ f[k\cdot v + 1]\\\\ f[2],\ f[v + 2],\ f[2\cdot v + 2],\ f[3\cdot v + 2],\ …\ ,\ f[k\cdot v + 2]\\\\ …\\\\ f[j],\ f[v + j],\ f[2\cdot v + j],\ f[3\cdot v + j],\ …\ ,\ f[k\cdot v + j] \end{cases} $$
显而易见，$m = k\cdot v + j$，其中$j = m \ mod \ v$，即 $0≤j<v$，如果 $j==v$ ，则 $f[2\cdot v] == f[v + j]$ ，显然不需要重复更新，$j > v$ 同样可以被其他选法所代替

我们可以把集合划分为 $j$ 类，这里的 $j$ 可以看成是考虑 $[0, v - 1]$ 的体积模数，每一类中都是在同类之间转换得到的，每一个物品都有像这样 $j$ 类的集合，而所有集合都会更新 $f[0..m]$ ，即：

多重背包分析

因此可以维护一个单调队列来得出结果
$$ \begin{cases} f[j] = f[j]\\\\ f[j + v] = max(f[j] + w, f[j + v])\\\\ f[j + 2v] = max(f[j] + 2w, f[j + v] + w, f[j + 2v])\ \ max(在j体积状态的基础上加上2w，在j+v体积上加w，原本j+2v状态)\\\\ f[j + 3v] = max(f[j] + 3w, f[j + v] + 2w, f[j + 2v] + w, f[j + 3v])\\\\ … \end{cases} $$
由于在下一次取最大值的时候，前面的状态都需要加上一个 $w$，这样无法很好利用单调队列来做，需要将其转换
$$ \begin{cases} f[j] = f[j]\\\\ f[j + v] = max(f[j],\ f[j + v] - w) + w\\\\ f[j + 2v] = max(f[j],\ f[j + v] - w,\ f[j + 2v] - 2w) + 2w\\\\ f[j + 3v] = max(f[j],\ f[j + v] - w,\ f[j + 2v] - 2w,\ f[j + 3v] - 3w) + 3w\\\\ … \end{cases} $$
这样能保证每次入队的值是 $f[k \cdot v + j] - k \cdot w$

所需维护的队列：$(f[j],\ f[j + v] - w,\ f[j + 2v] - 2w,\ …\ f[j + kv] - kw)$

单调队列问题

存的是体积 $j$ ，这里体积即为 $f$ 下标
单调性：降序

AcWing 6. 多重背包问题 III

多重背包Ⅰ裸题：

《信息学奥赛一本通》：AcWing 1019. 庆功会

分组背包

DP分析：

分组背包分析

特点：每一品种只能在其中一组这当中选，且最多选1次

基础题：AcWing 9. 分组背包问题

应用题：

《信息学奥赛一本通》：AcWing 1013. 机器分配

混合背包

有三类物品：

第一类物品只能用1次（01背包）
第二类物品可以用无限次（完全背包）
第三类物品最多只能用 $s_i$ 次（多重背包）

任意包含两类及以上即为混合背包

由于背包问题的状态转移都是独立的，且只和当前第 $i$ 件物品的状态有关，其类型是什么不影响后续状态转移，在状态转移时也与物品选择的顺序无关，所以直接混合即可。

由于01背包是多重背包的特殊类型（物品上限只有1件），所以01背包也可以归为多重背包来写

遍历物品
- 物品为完全背包
  - 做完全背包
- 物品为01或多重背包
  - 物品为01背包
    - 将数量设置为1
  - 做多重背包

有依赖的背包问题

有些物品需要选了特定的物品才能选，就像从属关系或主件附件一样

随从只有一层：AcWing 487. 金明的预算方案（二进制遍历附件即可）

随从有 $n$ 层：背包九讲：AcWing 10. 有依赖的背包问题（DFS + 分组背包）

二维费用背包问题

二维费用，顾名思义就是物品有两维的限制，可以理解为体积、重量的限制，按套路写就行，只是遍历体积的时候需要用遍历两维即可

背包九讲：AcWing 8. 二维费用的背包问题目标值就是 $f[V][M]$
《信息学奥赛一本通》：AcWing 1020. 潜水员状态是至少
《信息学奥赛一本通》：AcWing 1022. 宠物小精灵之收服 01二维费用，还需要找出价值最大时，体积最多是多少，读题有难度

背包求方案数

01背包求方案数
- 背包九讲：AcWing 11. 背包问题求方案数求最大价值的方案数
- 《算法竞赛进阶指南》：AcWing 278. 数字组合数字和等于 $M$ 的方案数
完全背包求方案数
- 《信息学奥赛一本通》：AcWing 1021. 货币系统面值等于 $m$ 的方案数
- NOIP 2018 提高组：货币系统进阶：AcWing 532. 货币系统贪心，系统的数字中能用n个系统中的数字表示，则可将其约掉（读题有点难）

背包求具体方案

动态规划在状态转移的时候要作出决策，而当我们求具体方案的时候，我们需要知道每一步作出的是什么决策，也就知道了每一步的具体方案是什么了

两种方法：

做完DP后，遍历一遍状态，找出每一步作出的决策是什么，从哪个状态转移过来的
开多一个与状态同维的数组，在DP状态转移时，用数组存下当前的决策，然后用dfs输出

需要注意的是，求具体方案时，不能优化掉一维的数组空间

背包九讲：AcWing 12. 背包问题求具体方案

线性DP模型

通常在递推的时候有一个线性顺序关系，不同于背包问题，背包问题则与顺序无关

AtCoder C - 1111gal password

数字三角形

一般是像数字三角形那样有一个类似图，通常由某一个点转移过来的，则可转化为数字三角形模型

入门题：AcWing 898. 数字三角形

裸题：《信息学奥赛一本通》：AcWing 1015. 摘花生

《信息学奥赛一本通》：AcWing 1018. 最低通行费在摘花生的基础上多加了时间限制（分析发现是最短路原则），还加了判断边界才状态转移
《信息学奥赛一本通》，NOIP 2000 提高组：AcWing 1027. 方格取数两人同时摘花生的最大和
- 两个人同时摘的话，状态需要四维 $f[x_1][y_1][x_2][y_2]$，可以优化掉一维 —> $f[k][x_1][x_2]$ ，其中$k = x_1 + y_1 = x_2 + y_2$
- 状态表示：路径长度为 $k$，第一条路线到 $x_1=i$，第二条路线到 $x_2=j$ 的所有方案
- 两个人的走的路径方案同时转移到一个状态上
- 两个人则有四种情况：
  - 两个人同时走到一个格子上 $x_1 == x_2 \&\& y_1 == y_2$
    - 方格数只取一次
  - 两个人不同时走到一个格子上
    - A从上面过来，B从上面过来
    - A从左面过来，B从左面过来
    - A从上面过来，B从左面过来
    - A从左面过来，B从上面过来
《算法竞赛进阶指南》，NOIP2008提高组，Google面试题：AcWing 275. 传纸条也是同时走的情况

最长上升子序列

最长上升子序列Ⅰ

通常都有单调性，或在某个部分有单调性（严格大于或严格小于），且是子序列的形式，则可转化为最长上升/下降子序列模型

套路：

遍历 $n$ 个元素
- 遍历开头元素 ~ 第 $n$ 个元素
  - 满足单调性 ==> 状态转移

模板题：AcWing 895. 最长上升子序列 $O(n^2)$

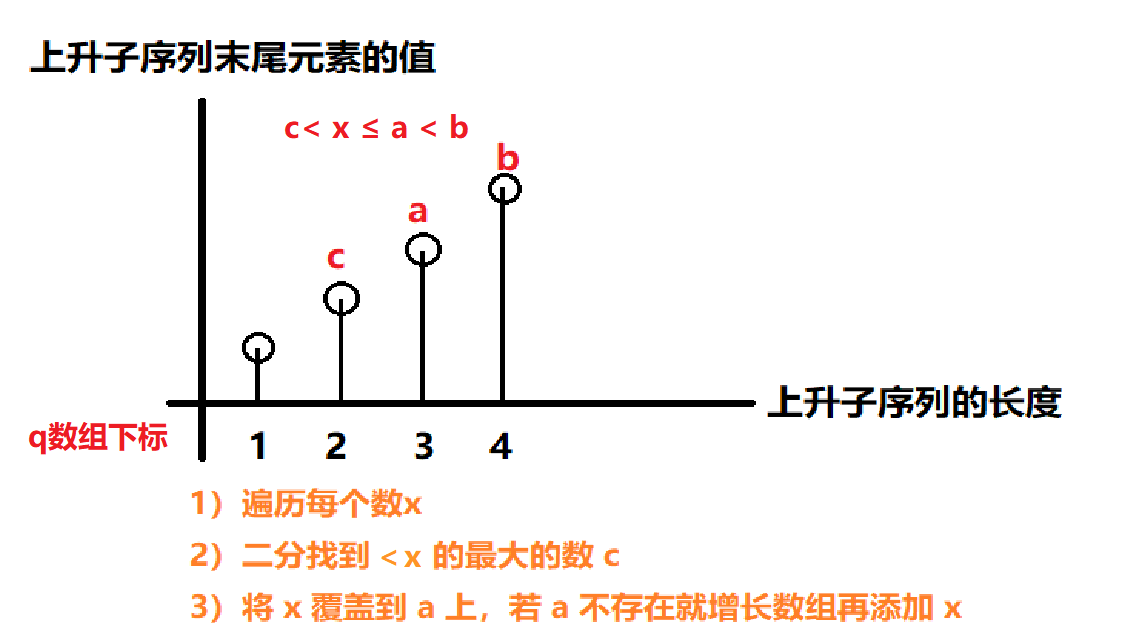
优化 $O(nlogn)$：AcWing 896. 最长上升子序列 II 贪心 + DP + 二分，同时还可以把最长上升子序列给存下来

思路：上升子序列尽可能的存较小的数，⌈较小的数后面接的数的范围⌋ 比 ⌈较大的数后面接的数的范围⌋ 大

贪心思路：

开一个数组 $q[N]$，用以存储最长上升子序列

遍历每个数 $x$

利用二分查找大于 $x$ 的第一个数

情况1：能找到大于 $x$ 的第一个数，则将此位置更新成 $x$

情况2：不能找到大于 $x$ 的第一个数，则在数组后添加

这样更大的数就被更新成更小的数，而后面就能接入更多的数

由于存在找不到大于 $x$ 的情况，而且找到的下标只会在 $[l, r]$ 中，所以无法实现在末尾添加新的 $x$，则可以先找小于 $x$ 的第一个数，然后更新其后一个数即可。

图借gyh

裸题：《信息学奥赛一本通》：AcWing 1017. 怪盗基德的滑翔翼
- 做一遍最长上升子序列，再做一遍最长下降子序列，然后遍历各点取 $max$
《信息学奥赛一本通》 , 第六届北京大学程序设计大赛暨ACM/ICPC选拔赛：AcWing 1014. 登山
- 两种做法：
  - 同时做单调上升下降
    - 开两个数组 $up$ 和 $down$ ，存储以第 $i$ 个数结尾的上升 / 下降子序列
    - 每次先更新上升的情况，再更新下降的情况，更新下降情况时，有两种情况
      - 情况1：以第 $j$ 个数为结尾的最长下降子序列后面接第 $i$ 个数，即 $down[j] + 1$
      - 情况2：以第 $j$ 个数为结尾的最长上升子序列后面接第 $i$ 个数，即第 $i$ 个数为下降的第一个山头，$up[j] + 1$
      - 两种情况取 $max$
  - 先做单调上升再做单调下降（因为上升顺序与下降顺序无关，相互独立的，但相互影响）
    - 开两个数组分别存最长上升子序列和最长下降子序列
    - 遍历取一个 $max$
NOIP2004提高组：AcWing 482. 合唱队形
- 左、右个做一遍最长上升子序列，然后用总人数减取俩最长的序列数
《信息学奥赛一本通》：AcWing 1012. 友好城市（要做转化）
- 以南岸城市排序，然后求北岸最长上升子序列
《信息学奥赛一本通》：AcWing 1016. 最大上升子序列和
- $f[i]$ 表示最长上升子序列和
- 维护一个最大值
《信息学奥赛一本通》 , NOIP1999：AcWing 1010. 拦截导弹贪心 + DP
- 第一问：经典最长上升子序列
- 第二问：类似最长上升子序列优化的贪心优化（因为每次存入的是大于等于 $x$ 的第一个数，即此数 $x$ 接在了能接的最前位置）
  - 新开一个数组 $g$ 存每一个上升子序列的尾值
  - 每次找到 $g$ 中大于等于 $x$ 的第一个数
  - 若 $x$ 大于 $g$ 中的每个数，则新开一个上升子序列，即存入 $g$ 数组最后
  - $g$ 数组大小即为答案
《算法竞赛进阶指南》：AcWing 187. 导弹防御系统贪心 + DP + DFS
- 此题为拦截导弹升级版
- 因为可以用上升 / 下降系统来拦截导弹，所以只能爆搜或迭代加深法来枚举每一种情况，这里用爆搜分析思路
  - 全局记录最小值
  - 判断退出：
    - 当前枚举点数 == 所以点数 —> 更新最小值
  - 剪枝：
    - 上升和下降系统 > 最小值 ----> 退出
  - 考虑用上升拦截系统来拦截第 $u$ 个导弹
  - 考虑用下降拦截系统来拦截第 $u$ 个导弹
- 记得恢复现场

最长公共子序列

实际上是有四种情况

最长公共子序列四种情况

但由于情况1可以归类到情况2和情况3中，因为 $a[i]!=b[j]$ 时，这两种情况会有重叠，所以可以忽略掉第一种情况，至于有重复，没有关系，因为是求最值

模板题：AcWing 897. 最长公共子序列

《算法竞赛进阶指南》：AcWing 272. 最长公共上升子序列
- 本题是最长上升子序列（LIS）和最长公共子序列（LCS）的结合体（LCIS）
- 状态表示：所有以 $a$ 的前 $i$ 个数，和以 $b$ 的前 $j$ 个数构成的，且以 $b[j]$ 为结尾的最长上升公共子序列
- 性质：包含 $a[i]$ 一定有 $a[i]==b[j]$
- 可以用一个 $maxl$ 来记录前 $i$ 个数和前 $j$ 个数的最长上升公共子序列
```
for (int i = 1; i <= n; i ++ )
{
    for (int j = 1; j <= n; j ++ )
    {
        f[i][j] = f[i - 1][j];
        if (a[i] == b[j])
        {
            int maxl = 1;
            // 可以发现当a[i] == b[j]时，求其f[i - 1][1 ~ j - 1] + 1的前缀和最大值maxl
            for (int k = 1; k < j; k ++ )
                if (a[i] > b[k]) // a[i] == b[j]
                    maxl = max(maxl, f[i - 1][k] + 1);
            f[i][j] = max(f[i][j], maxl);
        }
    }
}
```
- 可以进行优化，可以直接把一层循环优化掉，可以发现前缀和用到的是上一层的 $f$ ，即 $f[i - 1][\ ]$ ，而 $a[i]$ 和 $b[j]$ 都是本层的，由于 $b[k]$ 是 $b[1..j - 1]$ ，若包含 $a[i]$ 则一定更新，若不包含 $a[i]$ 那maxl也不会被用于更新，也就是说假设当前包含 $a[i]$ 然后求前缀和最大值，若实际上不包含，则不更新，若包含，则用 $maxl$ 更新，若更新，必然有 $a[i] == b[j]$ ，而当前上升子序列的尾值为 $a[i]$
```
for (int i = 1; i <= n; i ++ )
{
    int maxl = 1;
    for (int j = 1; j <= n; j ++ )
    {
        f[i][j] = f[i - 1][j];
        if (a[i] == b[j]) f[i][j] = max(f[i][j], maxl);
        if (a[i] > b[j]) maxl = max(maxl, f[i - 1][j] + 1); // 求前缀和最大值
    }
}
```

最小操作数

这类问题通常是给你几个操作，然后要你操作一种东西变成某种东西的最小次数

通常需要分析一下每种操作，然后按操作来分类

最小操作数

模板题：AcWing 902. 最短编辑距离

这里考虑最后一步，如图分析：

最小操作数分析

应用题：AcWing 899. 编辑距离

状态机模型

与前面的动态规划有点不太一样，状态机像是一个路径一个状态，将状态细分，同时需要记录当前细分到的状态，我认为是利用状态划分集合，需要注意的是，状态机需要设定一个入口和出口，入口即如何初始化，出口即目标值是什么，

下面一题一题分析了解状态机

《信息学奥赛一本通》：AcWing 1049. 大盗阿福

一般先设置$f$ 数组为$-INF或INF$ ，然后再初始化入口的合法状态

这里入口即是$f[i][0] = 0$，出口即 $f[n][0]$ 和 $f[n][1]$

可以利用类似01背包第一种优化方式优化空间
LeetCode：AcWing 1057. 股票买卖 IV

求最大值，同样需要先设置$-INF$ ，这里入口是 $f[i][0][0] = 0$，即当经过 $i$ 天，不交易且不持股的利润为0

理论上⌈持股时⌋和⌈没持股时⌋都是出口，但持股又不卖出，绝对亏本，所以不用考虑

由于不一定交易 $k$ 次利润最大，所以需要在 $f[n][j][0]$ 取一个 $max$

同样可以用滚动数组来优化空间
LeetCode：AcWing 1058. 股票买卖 V

求最大值，同样需要先设置 $-INF$，这里入口是 $f[0][2] = 0$，同时还需要初始化 $f[0][1] = 0$，出口是 $f[n][0]$ 和 $f[n][1]$

同样可以用滚动数组优化空间
IndeedTokyo2019校招笔试题：AcWing 1052. 设计密码
KMP状态机，$f[i][j]$ 表示已经生成 $i$ 位密码，且第 $i$ 位匹配到子串的字符后缀位置为 $j$ 的方案数

生成第 $i$ 位时，每次枚举当前位置的字符（a ~ z），KMP匹配母串的最大位置 $u$

按照KMP图的跳跃方式，每次跳跃到匹配的最大位置，从位置 $j$ 跳跃到位置 $u$ ，则用位置 $j$ 的状态更新位置 $u$ 的状态

两种状态：
- 模式串与枚举的字符匹配：$f[i - 1][u]$，（$u=j + 1$）
- 模式串与枚举字符串不匹配： $f[i - 1][u]$，（$u = ne[u]$）

状态压缩DP

利用二进制数，将动态规划中的状态数组进行压缩，通过二进制来进行位运算。

具体就是用二进制数把状态表示出来，然后枚举状态和转移状态

如果n比较小的话，可以考虑用状态压缩来做

状压DP一般分为：

棋盘式
集合型

棋盘式

一般需要预处理，把不合法的情况筛选掉，然后再做DP

常用套路：

遍历行（列）
- 遍历合法情况
  - 遍历合法情况转移

《信息学奥赛一本通》，SGU223，SCOI2005：AcWing 1064. 小国王（井字形填法）

$f[N][K][M]$：所有只摆前 $i$ 行，且国王数不超过 $k$ ，且当前状态为 $j$ 的所有摆法

先预处理出所有合法情况

筛掉本行不合法情况

筛掉行与行间不合法情况

由于这里有国王限制，模仿背包问题的做法，把国王看成背包容量即可

第一种做法（直接用二进制表示的情况来表示状态）：（这里利用率滚动数组，不会的话往上翻01背包优化）
//DP
f[0][0][0] = 1; // 一行不摆，且一个国王不用的方案数为1
for(int i = 1; i <= n + 1; i ++) // 枚举每行
    for(int j = 0; j <= m; j ++) // 枚举国王
        // 枚举状态转移
        for(auto a : state) // 枚举本行合法情况
            for(auto b : edstate[a]) // 枚举从情况a能转移的合法行
            {
                int c = cnt[a];
                if(j >= c) f[i & 1][j][b] += f[i - 1 & 1][j - c][a]; // 从a转移至b
            }
cout << f[n + 1 & 1][m][0]; // 技巧，当摆到n + 1行时，一个都不摆
第二种做法（利用下标索引二进制的情况来表示状态）：
//DP
f[0][0][0] = 1; // 一行不摆，且一个国王不用的方案数为1

for(int i = 1; i <= n + 1; i ++) // 枚举每行
    for(int j = 0; j <= m; j ++) // 枚举国王
        // 枚举状态转移
        for(int a = 0; a < state.size(); a++) 
            for(auto b : edstate[a])
            {
                int c = cnt[state[a]];
                if(j >= c) f[i & 1][j][b] += f[i - 1 & 1][j - c][a]; // 从a转移至b (用其下标表示)
            }
cout << f[n + 1 & 1][m][0]; // 小技巧，当摆到n + 1行时，一个都不摆
需要注意的是：不同的做法在筛选时存的东西也不同。我个人更喜欢直接用二进制表示状态

《算法竞赛进阶指南》：AcWing 327. 玉米田（十字形填法）
- 状态表示：$f[N][M]$ 所有只摆前 $i$ 行，且当前行的状态为 $j$ 的方案数
- 状态转移：$f[i - 1][u1]—>f[i][u]$ ，$u$ 为本行情况，$u1$ 前一行情况
- 这题需要注意的是：每行的合法情况都不同，因为有坏死的玉米地，我们可以在DP的时候判断一下不能转移即可
- 预处理筛选合法情况
  - 筛选掉本行不合法情况
  - 筛选掉行与行间的不合法情况
- 用二进制来存图后续做DP好判断
- 如果想从 $a$ 转移到 $b$ ，你需要判断 $b$ 是否合法
《算法竞赛进阶指南》, NOI2001：AcWing 292. 炮兵阵地（十字扩展多一格）
- 可以说是玉米田的升级版
- 多加一维状态来存储前 $i - 1$ 行即可
- $f[N][M][M]$：所有只摆前 $i$ 行，且当前行的状态为 $j$ ，且前一行的状态为 $k$ 的方案数
- 状态转移 $f[i - 1][u1][u2] —> f[i][u][u1]$ ，$u$ 为本行情况，$u1$ 前一行情况，$u2$ 前二行情况
- 预处理筛选合法情况：
  - 筛掉本行不合法情况
  - 筛掉行与行间不合法情况
- 同样用二进制来存图
- 需要注意的是
  - DP时需要判断第 $i$ 行和第 $i -2$ 行是否合法
《算法竞赛进阶指南》，模板题：AcWing 291. 蒙德里安的梦想（横向、纵向填法）
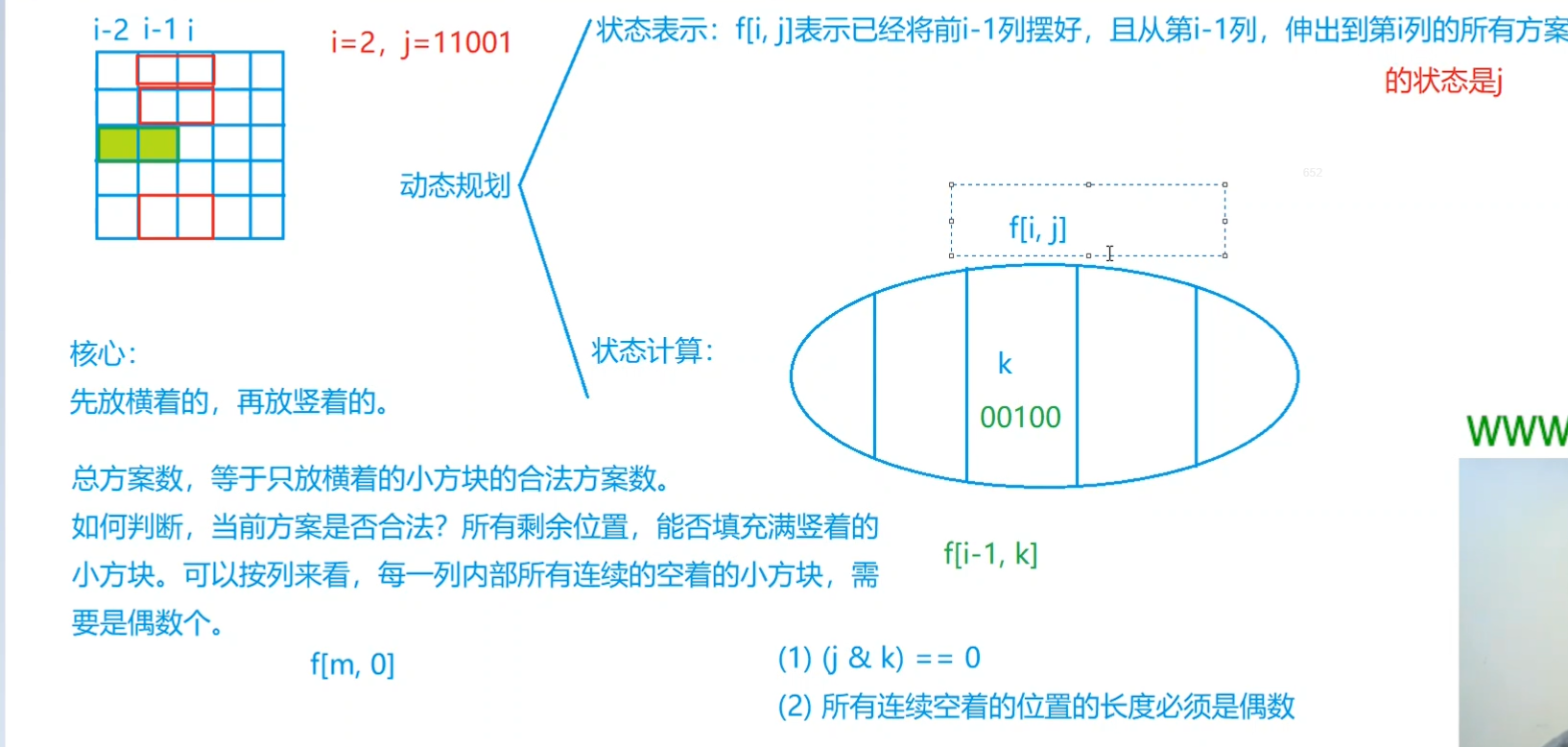
- 按列来划分
- 先摆完所有横向的方块，摆完后，纵向的方块就只有一种摆法，所以总方案数即为摆放横向方格的方案数
- 预处理筛选合法情况
- 筛掉连续奇数个0的情况，防止纵向方块放不进去
- 为了防止横向的方块冲突，固定让方块右边为1，左边为0，即表示从第 $i - 1$ 列伸到第 $i$ 列的方块
- (j & k) == 0 第 $i - 1$ 列与第 $i$ 列没有重叠摆放
- st[j | k] 表示第 $i - 1$ 列横插到第 $i$ 列有没有造成连续奇数个0的情况