前缀和详解
一、一维前缀和
1. 应用场景
对于一个长度为 n 的 整数序列 a[N]，给定一个区间 [ L , R ]
计算原序列中从第 L 个数到第 R 个数的和 Sum 。( 注意 下标从 1 开始 )
$$
\begin{array}{l}
整数序列:\{ \;{a_1}\;,\;{a_2}\;,\;{a_3}\;,\;…\;,\;{a_L}\;,\;{a_{L + 1}}\;,\;…\;,\;{a_R}\;,\;…\;{a_{\rm{N}}}\} \\\\
Sum\;[\;L\;,\;R\;]\; = \;{a_L}\; + \;{a_{L + 1}}\; + \;…\; + \;{a_{R - 1}}\; + \;{a_R}
\end{array}
$$
题源：795. 前缀和 - AcWing题库
2. 暴力解法
使用循环直接求出 Sum
int sum = 0;
for( int i = L; i <= R; i++ ) sum += a[i];
说明：这样计算区间内整数之和的 时间复杂度 为 O(n) ，
当询问的次数很多时，要花费大量时间。
而使用 前缀和 的方式求和，能解决让这类 区间求和 询问的时间复杂度减小到 O(1)
3. 一维前缀和详解
作用 ：快速地求出原数组中某个区间中的数字之和。
一维 前缀和 数组 S[N]：
$$
\begin{array}{l}
数组 :\{ \;{a_1}\;,\;{a_2}\;,\;{a_3}\;,\;…\;,\;{a_L}\;,\;{a_{L + 1}}\;,\;…\;,\;{a_R}\;,\;…\;{a_{\rm{n}}}\} \\\\
前缀和数组 :\;S\;[N]\\\\
S\;[\;0\;] = 0\\\\
S\;[\;1\;] = {a_1}\\\\
S\;[\;2\;] = {a_1} + \;{a_2}\\\\
S\;[\;3\;] = {a_1} + \;{a_2} + \;{a_3}\\\\
......\\\\
S\;[\;n\;] = {a_1} + \;{a_2} + \;{a_3} + \;…\; + \;{a_n}
\end{array}
$$
注意事项：特别设置 S[0] == 0 。
前缀和数组计算方式 ：$S\;[\;n\;]\;\; = \;\;S\;[\;n - 1\;]\; + \;{a_n}$
$$
\begin{array}{l}
S\;[\;3\;]\;\; = \;\;{a_1} + \;\;{a_2} + \;\;{a_3}\;\; = \;\;S\;[\;2\;]\; + \;{a_3}\;\;\\\\
S\;[\;4\;]\;\; = \;\;{a_1} + \;\;{a_2} + \;\;{a_3} + \;\;{a_4}\;\; = \;\;S\;[\;3\;]\; + \;{a_4}\;\;
\end{array}
$$
代码实现 ：
for( int i = 1; i <= n; i++ ) s[i] = s[i - 1] + a[i];
// 计算 前缀和数组 的时间复杂度为 O(n)
说明 ：
只要一次 O(n) 的计算，能让 之后所有 的计算区间内元素和的询问的时间复杂度变为 O(1) 。
而用循环 直接计算 区间内元素之和，每次计算时间复杂度都是 O(n) 。
用前缀和解决数组区间内元素求和问题 [ L , R ] ：
$Sum\;[\;L\;,\;R\;]\;\; = \;\;S\;[\;R\;]\;\; - \;\;S\;[\;L - 1\;]\;$
( 只通过两个数字相减，时间复杂度为 O(1) )
$$
\begin{array}{l}
推导 : Sum\;[\;L\;,\;R\;]\;\;\\\\
= \;\;{a_L}\; + \;{a_{L + 1}}\; + \;…\; + \;{a_{R - 1}}\; + \;{a_R}\\\\
= \;\;[\;(\;{a_1}\; + \;{a_2}\; + \;…\; + \;{a_{L - 1}}\;)\; + \;{a_L}\; + \;…\; + \;{a_R}\;]\;\; - \;\;(\;\;{a_1}\; + \;{a_2}\; + \;…\; + \;{a_{L - 1}})\\\\
= \;\;S\;[\;R\;]\;\; - \;\;S\;[\;L - 1\;]\;
\end{array}
$$
$$ \begin{array}{l} 举例 : Sum\;[\;3\;,\;4\;]\\\\ = \;\;{a_3}\; + \;{a_4}\\\\ = \;\;[\;(\;{a_1}\; + \;{a_2}\;)\; + \;{a_3}\; + \;{a_4}\;]\; - \;(\;{a_1}\; + \;{a_2}\;)\\\\ = \;\;S\;[\;4\;]\;\; - \;\;S\;[\;2\;]\; \end{array} $$
说明：原数组与前缀和数组下标从 1 开始的原因：
即要求数组 array[1] == a1 ， S[1] == a1 ，S[0] == 0
-
统一区间内求和的公式
对于任意的区间
[ L , R ]，$Sum\;[\;L\;,\;R\;]\;\; = \;\;S\;[\;R\;]\;\; - \;\;S\;[\;L - 1\;]\;$举例 ：对于区间
[ 1 , 5 ]，$Sum\;[\;1\;,\;5\;]\;\; = \;\;S\;[\;5\;]\;\; = \;\;S\;[\;5\;]\;\; - \;\;S\;[\;0\;]\;$ 。这样就不用特殊处理像上述例子中的边界问题
-
便于理解
( 1 ) 第x个数的下标为x；
( 2 ) 前x个数的和为S[x]。
4. 函数模板 —— 一维前缀和
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
scanf( "%d%d", &n, &m );
// a[0] == 0，下标从 1 开始输入
for( int i = 1; i <= n; i++ ) scanf("%d", &a[i]);
// s[0] == 0，下标从 1 开始计算
for( int i = 1; i <= n; i++ ) s[i] = s[i - 1] + a[i]; // 计算前缀和
while( m-- )
{
int l, r;
scanf( "%d%d", &l, &r );
printf( "%d\n", s[r] - s[ l - 1 ] ); // 区间和的计算
}
return 0;
}
注意 ：输入数据和计算前缀和时，下标从 1 开始。
二、子矩阵的和 ( 二维前缀和 )
1. 应用场景
对于 $N \times M$ 的二维数值矩阵 a[N][N]，
给定两个点所在的坐标 $(\;{x_1}\;,\;{y_1}\;)\;\;,\;\;(\;{x_2}\;,\;{y_2}\;)$ ，
计算以这两点为 对角线 形成的 子矩形 中的所有元素的和。
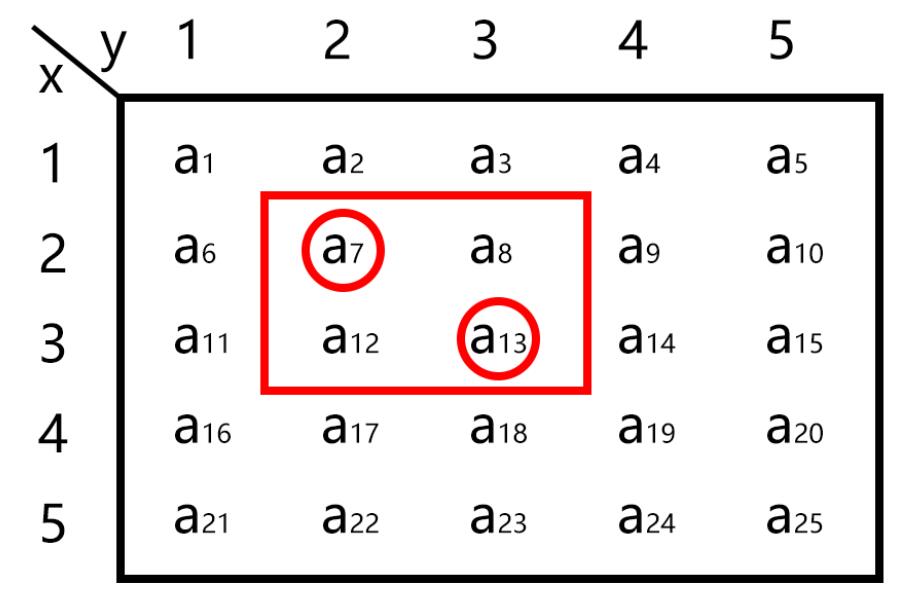
举例 ：给定坐标 ( 2 , 2 ) ，( 3 , 3 )
$Sum\;\; = \;\;{a_7}\; + \;{a_8}\; + \;{a_{12}}\; + \;{a_{13}}\;$
{:height=”40%” width=”40%”}
2. 暴力解法
int sum = 0;
for( int i = x1; i <= x2; i++ )
for( int j = y1; j <= y2; j++ )
sum += a[i][j];
与一维前缀和类似，使用 双重循环 直接求解，时间复杂度 为 O( n^2 )
但使用 前缀和 求解，时间复杂度为 O(1)
3. 二维前缀和详解
作用 ：快速求出二维子矩阵中的数字之和。
二缀和数组 S[x][y]：
表示以坐标 ( x , y ) 为 右下角 坐标，
( 1 , 1 ) 为 左上角 坐标的子矩阵中所有元素之和。
注意 ：与一维前缀和一样，下标从 s[1][1]开始
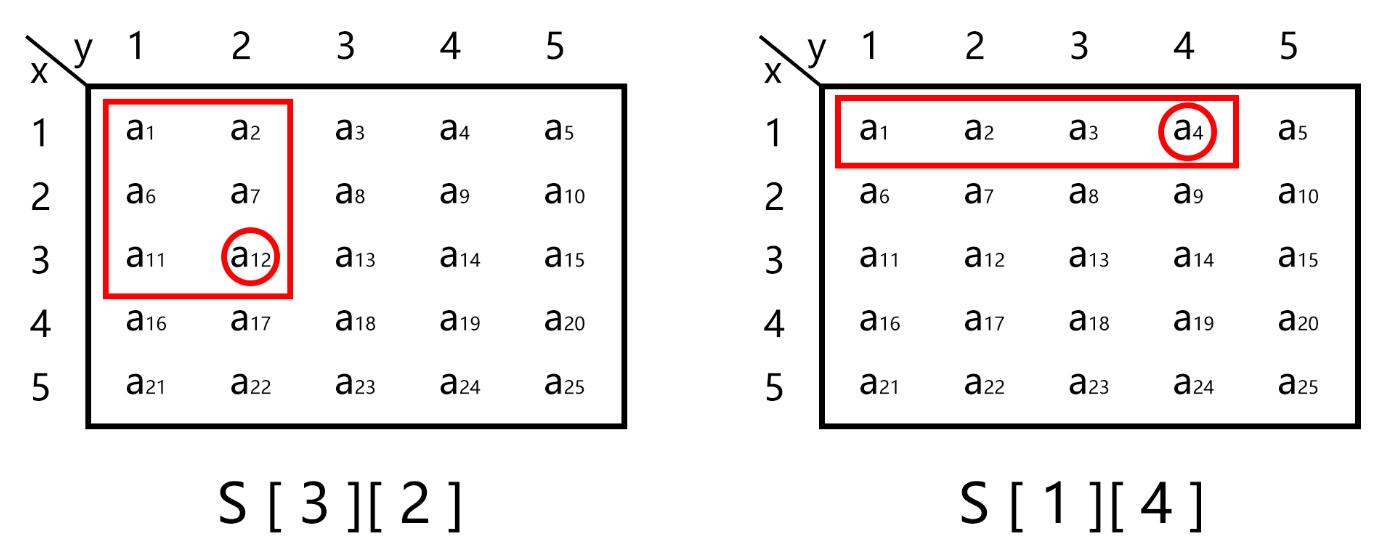
举例 ：$S\;[\;3\;][\;2\;]\;\; = \;\;{a_1} + \;\;{a_2} + \;\;{a_6}\; + \;\;{a_7} + \;\;{a_{11}}\; + \;\;{a_{12}}\;$
$S\;[\;1\;][\;4\;]\;\; = \;\;{a_1} + \;\;{a_2} + \;\;{a_3}\; + \;\;{a_4}$
{:height=”80%” width=”80%”}
二维前缀和 S[N][N] 的计算
$S\;[\;i\;][\;j\;]\; = {\rm{ }}S\;[\;i\;][\;j - 1\;]{\rm{ }} + {\rm{ }}S\;[\;i - 1\;][\;j\;]{\rm{ }} - {\rm{ }}S\;[\;i - 1\;][\;j - 1\;]{\rm{ }} + {\rm{ }}a\;[\;i\;][\;j\;]$
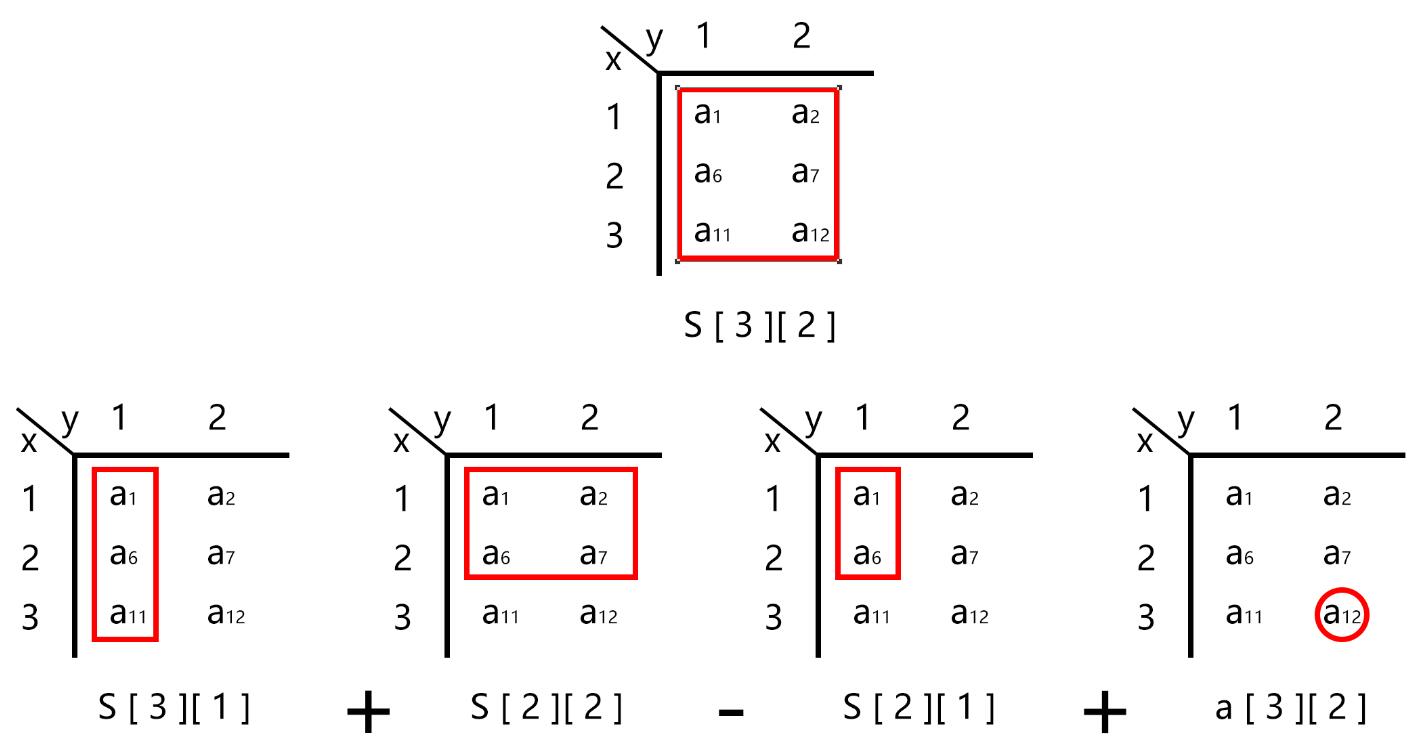
举例 ：计算 $S\;[\;3\;][\;2\;]$
$$
\begin{array}{l}
S\;[\;3\;][\;1\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_6} + \;\;{a_{11}}\\\\
S\;[\;2\;][\;2\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_2} + \;\;{a_6}\; + \;\;{a_7}\\\\
S\;[\;2\;][\;1\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_6}\\\\
\\\\
S\;[\;3\;][\;2\;]{\rm{ }} = {\rm{ }}S\;[\;3\;][\;1\;]{\rm{ }} + {\rm{ }}S\;[\;2\;][\;2\;]{\rm{ }} - {\rm{ }}S\;[\;2\;][\;1\;]{\rm{ }} + {\rm{ }}a\;[\;3\;][\;2\;]\\\\
= {a_1} + \;\;{a_2} + \;\;{a_6}\; + \;\;{a_7} + \;\;{a_{11}}\; + \;\;{a_{12}}
\end{array}
$$
{:height=”95%” width=”95%”}
用前缀和计算子矩阵中数值之和
给定两个点所在的坐标 $(\;{x_1}\;,\;{y_1}\;)\;\;,\;\;(\;{x_2}\;,\;{y_2}\;)$
$Sum\;\; = \;\;S\;[\;{x_2}\;][\;{y_2}\;]{\rm{ }} - {\rm{ }}S\;[\;{x_2}\;][\;{y_1} - 1\;]{\rm{ }} - {\rm{ }}S\;[\;{x_1} - 1\;][\;{y_2}\;]{\rm{ }} + {\rm{ }}S\;[\;{x_1} - 1\;][\;{y_1}{\rm{ }} - {\rm{ }}1\;]$
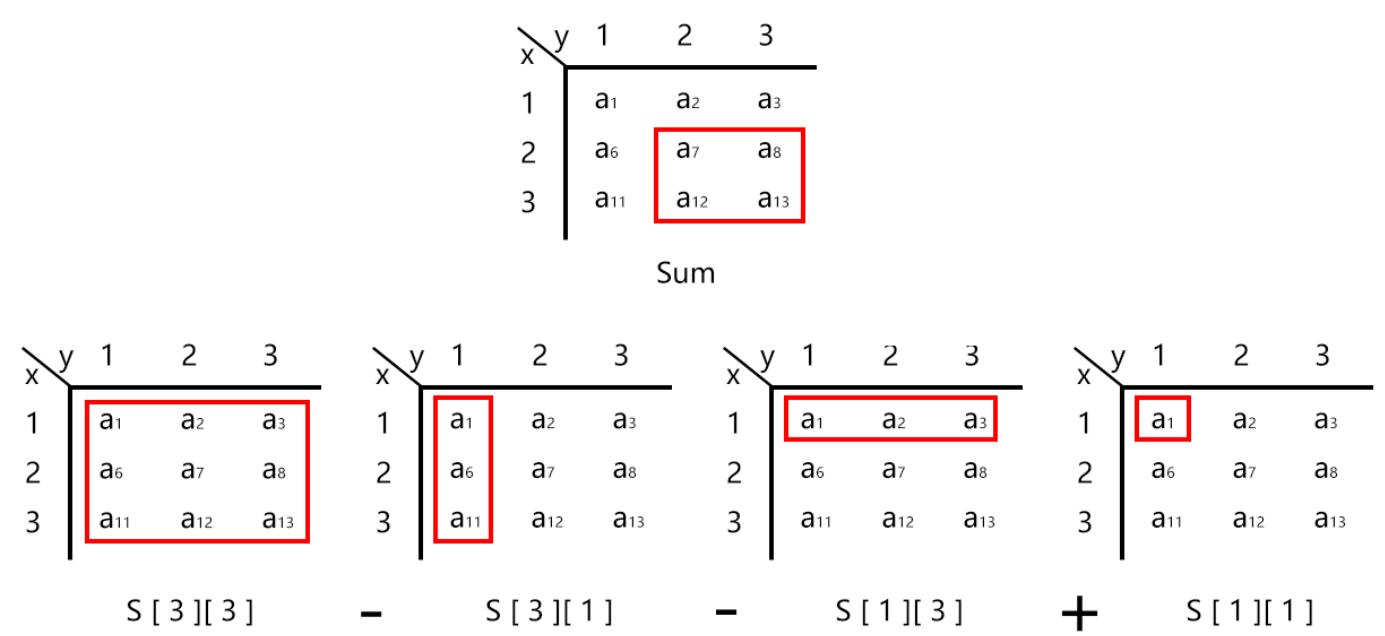
举例：给定坐标 $(\;2\;,\;2\;)\;,\;(\;3\;,\;3\;)$
$$
\begin{array}{l}
S\;[\;3\;][\;3\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_2} + \;\;{a_3}\; + \;\;{a_7} + \;\;{a_8} + \;\;{a_{11}}\; + \;\;{a_{12}} + \;\;{a_{13}}\\\\
S\;[\;3\;][\;1\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_6} + \;\;{a_{11}}\\\\
S\;[\;1\;][\;3\;]{\rm{ }} = {\rm{ }}{a_1} + \;\;{a_2} + \;\;{a_3}\\\\
S\;[\;1\;][\;1\;]{\rm{ }} = {\rm{ }}{a_1}\\\\
\\\\
Sum\;\; = \;\;S\;[\;3\;][\;3\;]{\rm{ }} - {\rm{ }}S\;[\;3\;][\;1\;]{\rm{ }} - {\rm{ }}S\;[\;1\;][\;3\;]{\rm{ }} + {\rm{ }}S\;[\;1\;][\;1\;]\\\\
= \;\;{a_7} + \;\;{a_8} + \;\;{a_{12}}\; + \;\;{a_{13}}
\end{array}
$$
{:height=”95%” width=”95%”}
4. 函数模板 —— 二维前缀和
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
// a[0][0] == 0，下标从 a[1][1] 开始输入
for(int i =1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
// s[0][0] == 0，下标从 s[1][1] 开始计算
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
// 计算二维前缀和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
while(q--)
{
int x1, y1, x2, y2;
scanf( "%d%d%d%d", &x1, &y1, &x2,&y2 );
// 计算子矩阵的和
int sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
printf( "%d\n", sum );
}
return 0;
}
注意 ：输入数据和计算前缀和时，下标从 1 开始。
三、参考资料
y 总的课hh
（接受批评指正，欢迎交流补充~~ XD）
