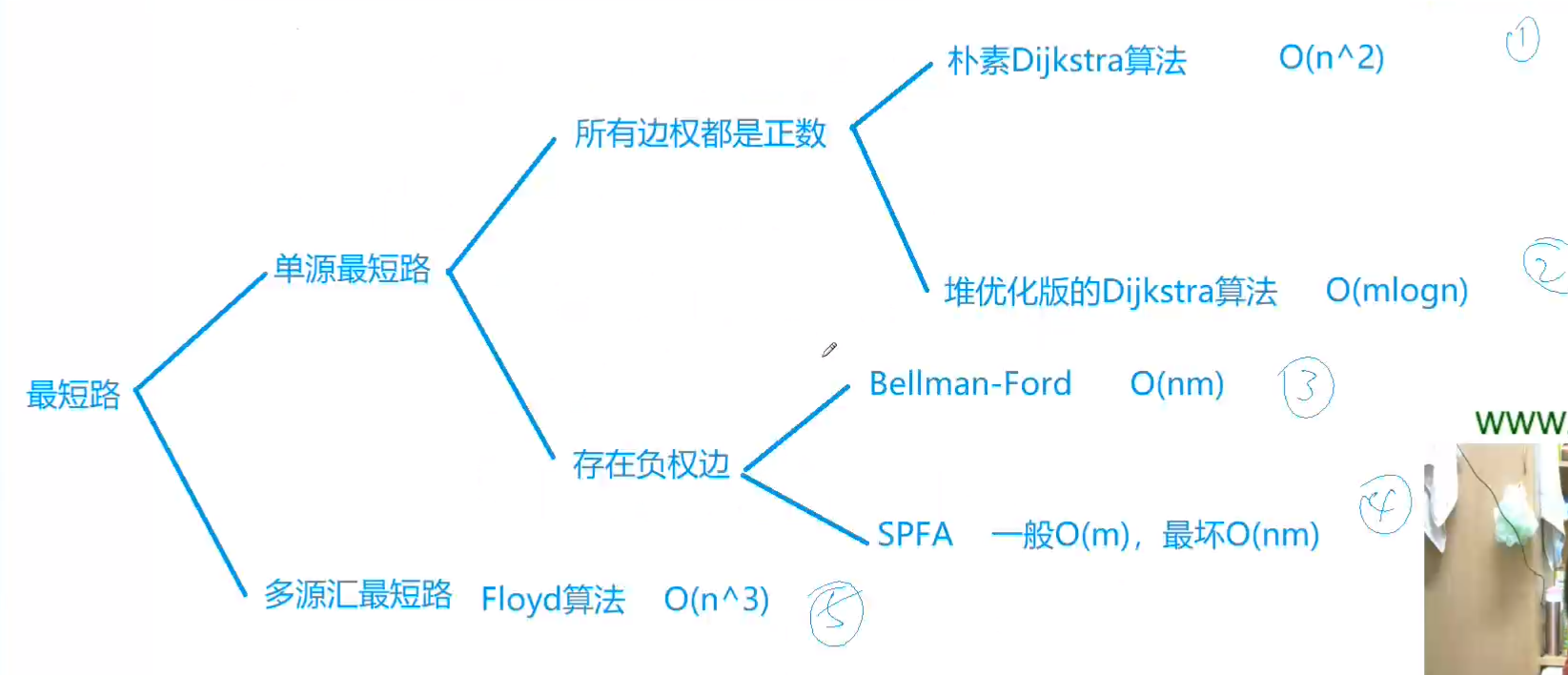
最短路
这里是四种常用最短路的代码和注释
- dijkstra
- dijkstra优先队列
- bellman_ford
- spfa
- floyd
dijkstra
最短路算法用于求某节点到另一节点的最短距离
dijkstra是一个最经典的最短路算法
在程序进行之前,我们需要先确定两个集合$d,st$。
$d[i]$存的是起点start~i的最短距离,$st[]$中存的是以遍历的点。
在图中,从起点开始遍历,通过寻找下一个距离最短(最近)的点,来更新$d$数组,那么最后$d$数组中的值就是最优解
图例

我们需要先确定建图方式
链表
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m; //点和边的数量
int d[N]; //最短距离
int h[N]; //以A为起点的有向边的链头
int e[N]; //以A为起点的有向边的B结点
int w[N]; //有向边AB的权值
int ne[N]; //链表中下一项的地址
int idx=0; //迭代器
int add(int a,int b,int c) //将权值为c边AB加入链表
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--)
{
int a,b,c; cin>>a>>b>>c;
add(a,b,c); add(b,a,c); //无向图需要建两次边
}
dijkstra();
for(int i=1;i<=n;i++) cout<<i<<" "<<d[i]<<" ";
}
邻接矩阵
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m; //点和边的数量
int d[N]; //最短距离
int g[N][N];
int main()
{
cin>>n>>m;
while(m--)
{
int a,b,c; cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c); //无向图需要建两次边
}
dijkstra();
for(int i=1;i<=n;i++) cout<<i<<" "<<d[i]<<" ";
}
下面为了方便,使用邻接矩阵进行存储
图中起点start=A,为了求出最小值,我们需要初始化$d$数组为正无穷INF
$d[start]=0;$
记住$d$数组存的是start到i的最小值
以上图为准我们进行推导:
$找到最小值d[A]=0;$
$更新H,E值得d[H]=2,d[E]=5;$
$下一步遍历$
$找到最小值d[H]=2$
$更新C,F值得d[C]=7,d[F]=5;$
$下一步遍历$
$找到最小值d[F]=5$
$更新C值得d[C]=6;$
$下一步遍历$
$找到最小值d[C]=6$
$所连接点都已是最小值$
$下一步遍历$
$找到最小值d[E]=5$
$所连接点都已是最小值$
$下一步遍历$
$所有点都已遍历,所以遍历结束$
经过验证,你就会发现$d$数组中存的确实是最小值
这种单调性可以保证其算法的正确性
此处是有向图
AC code O(n^2)
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
int g[N][N]; bool st[N];
int d[N];
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[1]=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||d[t]>d[j]))
t=j;
st[t]=true;
for(int j=1;j<=n;j++)
d[j]=min(d[j],d[t]+g[t][j]);
}
if(d[n]>=0x3f3f3f3f) return -1;
return d[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--){
int a,b,c; cin>>a>>b>>c;
g[a][b]=min(g[a][b],c);
}
cout<<dijkstra();
return 0;
}
dijkstra优先队列
因为dijkstra在寻找最近的点时,总是要将整个图遍历一遍
所以我们可以用堆(优先队列)来存储最近的点
但是需要注意一点,在优先队列中使用二元组时,堆会按第一个元素来排序,所以需要将$d$值放在前面
该处用链表存储
__AC code__O(m logn)
#include<bits/stdc++.h>
#define PII pair<int,int>
using namespace std;
const int N=200010;
int n,m;
int h[N],e[N],w[N],ne[N],idx;
int d[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int dijkstra()
{
memset(d,0x3f,sizeof d); d[1]=0;
priority_queue<PII,vector<PII>,greater<PII> > q; q.push({0,1});
while(!q.empty())
{
auto t=q.top(); q.pop();
int dist=t.first,f=t.second;
if(st[f]) continue; st[f]=true;
for(int i=h[f];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>dist+w[i])
{
d[j]=dist+w[i];
q.push({d[j],j});
}
}
}
if(d[n]>=0x3f3f3f3f) return -1;
return d[n];
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--){
int a,b,c; cin>>a>>b>>c;
add(a,b,c);
}
cout<<dijkstra()<<endl;
return 0;
}
但是你会发现一旦存在负权边,dijkstra却无法找到,那么要如何解决?
bellman_ford
虽说bellman_ford算法效率低下,但是求解有边数限制的最短路问题还是可以的
bellman_ford算法的思路就是不断的进行松弛操作,使每个点的$d$值最小
所谓松弛操作,就是代码中简洁的求最小值
distance[i]=min(distance[i],back[j]+w);
而在每轮松弛操作前,都要将$d$数组复制进$back$数组,这是为了避免特殊情况
先给出代码琢磨琢磨:
AC code O(mn)
#include<bits/stdc++.h>
using namespace std;
const int N=510,M=10010;
int n,m,k;
struct edge{
int sv,ev,w;
}e[M];
int d[N],backup[N];
int bellman_ford()
{
memset(d,0x3f,sizeof d);
d[1]=0;
for(int i=0;i<k;i++)
{
memcpy(backup,d,sizeof d);
for(int j=0;j<m;j++)
{
int a=e[j].sv,b=e[j].ev,w=e[j].w;
d[b]=min(d[b],backup[a]+w);
}
}
if(d[n]>=0x3f3f3f3f/2) return -0x3f3f3f3f; //负权边的扫雷方法
return d[n];
}
int main()
{
cin>>n>>m>>k;
for(int i=0;i<m;i++){
int a,b,c; cin>>a>>b>>c;
e[i]={a,b,c};
}
int ans=bellman_ford();
if(ans==-0x3f3f3f3f) cout<<"impossible";
else cout<<ans;
return 0;
}
其实不难发现,bellman_ford算法的核心部分和其他最短路算法是类似的,所以在此不去做过多解读
特殊情况
次数限制:1
边集:
a b w
1 2 1
1 3 3
2 3 1
可以把图画下来观察一下
我们可以发现,如果没有back数组,3结点的$d$值将等于2,因为在前面的松弛操作时,2的值已经被更新为1,
而如果再用2去更新3,那么就是第二次操作,将超出限制,且最小值为2,而正确答案是3。
Spfa
spfa算法的效率总是远比他的时间复杂度要快很多
基于bfs的spfa,在大部分情况下拥有O(n)的时间复杂度,算法也是很容易实现
spfa和dijkstra算法的思路是一样的,通过bfs的搜索,遍历并更新$d$数组以得到最优解。
所以我在dijkstra上的笔墨花的最多,因为算法是相通的
下面直接给出代码
AC code O(n),最坏O(nm)
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
int n,m;
int h[N],e[N],w[N],ne[N],idx;
int d[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int spfa()
{
memset(d,0x3f,sizeof d);
d[1]=0;
queue<int> q; q.push(1);
st[1]=true;
while(!q.empty())
{
int t=q.front(); q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>d[t]+w[i])
{
d[j]=d[t]+w[i];
q.push(j);
st[j]=true;
}
}
}
if(d[n]>=0x3f3f3f3f) return -0x3f3f3f3f;
else return d[n];
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--){
int a,b,c; cin>>a>>b>>c;
add(a,b,c);
}
int ans=spfa();
if(ans==-0x3f3f3f3f) puts("impossible");
else cout<<ans;
return 0;
}
推荐使用
Floyd
基于动态规划思想的多源汇最短路算法
所以直接上手动态规划的状态分析
以初三维分析:$f[k][i][j]$ 表示在前k个结点时i到j的最小值
那么有$f[k][i][j]=min(f[k-1][i][j],f[k-1][i][k]+f[k-1][k][j])$
分别表示前k-1个数中i到j的最小值和经过k点和不经过k点的和的最小值
通过分析可以降维(因为$f[k]只会和f[k-1]有关系$)
所以状态表示为$f[i][j]=min(f[i][j],f[i][k]+f[k][j]);$
AC code O(n^3)
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,m,k;
int d[N][N];
void floyd()
{
for(int f=1;f<=n;f++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][f]+d[f][j]);
}
int main()
{
memset(d,0x3f,sizeof d);
cin>>n>>m>>k;
while(m--){
int a,b,c; cin>>a>>b>>c;
d[a][b]=min(d[a][b],c);
}
floyd();
while(k--)
{
int x,y; cin>>x>>y;
if(x==y) puts("0"); //注意要搞特判
else if(d[x][y]>=0x3f3f3f3f/2) puts("impossible");
else cout<<d[x][y]<<endl;
}
return 0;
}
那么对最短路的分析,就到此为止了,后期还会更新一点内容
update


hh,没办法