矩阵的定义

$\space\space$一个m × n的矩阵就是m×n个数排成m行n列的一个数阵 矩阵可以用于批量解决一些线性问题 常见于递推的加速
另 1 × m的矩阵又叫做向量

矩阵乘法的定义

矩阵乘法的作用

$\space\space\space\space\space\space$在我们学习递推的过程中 (我们定义$S_k$为在k值的时候最终计算的值)我们经常会遇见很多$S_{k + 1}$ = $S_k$ × A 的递推式子常见的思路就是通过迭代或者循环来求得我们需要的结果 但在k为一个极大值的时候 即有可能TLE 所以我们需要考虑一个新的方法来加速递推
$\space\space\space\space\space\space$我们在考虑到我们给定的公式上$S_{k + 1}$ = $S_k$ × A 我们转化下递推形式$S_{k + 1}$ = $S_1$ × $A^k$ 我们惊奇的发现 在转化成通式后 神似一个qmi的式子 只不过此时是以矩阵为元素 而我们知道qmi的时间复杂度为O(logk) 极大的优化了时间复杂度

矩阵相乘

通式
$$ a_{ij} = \sum_{k = 1}^{n} b_{ik} * c_{kj} $$
写成矩阵的形式

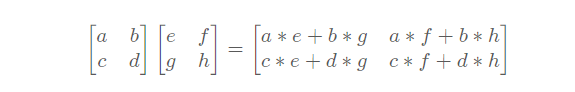
矩阵相乘性质

1. 矩阵乘法满足结合律 即$(A * B) * C = A * (B * C)$
2. 满足分配律 即$(A + B) * C = A * C + B * C$
3. 但不满足交换律 即 $A * B \not= B * A $

应用例题

1. 斐波那契前 n 项和

题意

$\space\space\space\space\space\space$输入 n 和 m，求 fn 的前 n 项和 $S_n$ mod m

分析

我们定义一个斐波那契矩阵F[i] = [f[i], f[i + 1], sum[i]]
我们对矩阵进行地推变换 F[i + 1] =[f[i + 1], f[i + 2], sum[i + 1]]
而从矩阵1 -> 2的变换 我们推出转置矩阵A =[[0, 1, 0], [1, 1, 0], [0, 1, 1]]//竖向保存矩阵 运算更直观
(注意 竖向考虑矩阵即相当于每项选取几个进行该新矩阵的拼凑)

A的注解

按照矩阵相乘的原理 对于F[i + 1]中的第一项f[i + 1]是由F[i]的f[i + 1]构成 所以对应A中的第一行[0, 1, 0]
而F[i + 1]中的f[i + 2]是由F[i]中的f[i] + f[i + 1]求和推出 所以对应[1, 1, 0]
F[i + 1]中的sum[i + 1]则由F[i]中的f[i + 1] + sum[i]求和构成 故对应[0, 1, 1]

那么求得之后 我们可以推出F[n] = f[1] * $A^n$$^-$$^1$
故而用快速幂求解 因为该式子的系数是f[1] 故我们将res初始化为f[1]即可

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 3;

int n, m;

void mul(int c[], int a[], int b[][N])
{
    int temp[N] = {0};
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ )
            temp[i] = (temp[i] + (LL)a[j] * b[j][i]) % m;

    memcpy(c, temp, sizeof temp);
}

void mul(int c[][N], int a[][N], int b[][N])
{
    int temp[N][N] = {0}; //定义一个新的矩阵 避免在mul中 c 与 a产生冲突
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ )
            for (int k = 0; k < N; k ++ )
                temp[i][j] = (temp[i][j] + (LL)a[i][k] * b[k][j]) % m;

    memcpy(c, temp, sizeof temp);
}

int main()
{
    cin >> n >> m;

    int f1[N] = {1, 1, 1};
    int a[N][N] = {
        {0, 1, 0},
        {1, 1, 1},
        {0, 0, 1}
    };

    n -- ;
    while (n)
    {
        if (n & 1) mul(f1, f1, a);  // res = res * a
        mul(a, a, a);  // a = a * a
        n >>= 1;
    }

    cout << f1[2] << endl;

    return 0;
}

2. 佳佳的斐波那契

佳佳的斐波那契题解

广义矩阵乘法

$\space\space\space\space\space\space$初步讲完了矩阵乘法 我们来涉及下广义矩阵乘法及其作用
我们定义行如 $$S_{k + 1} = S_k \bigodot A$$
即转化为一般是 $S_{k + 1} = S_1 * A^{\bigodot(k - 1)}$
$\space\space\space\space\space\space$因为满足结合律 我们任然可以通过矩阵快速幂来加速递推

应用例题

1. 定长最短路

牛站 题解

2. 定长路径统计

3. 限长路径统计