树状数组

特点

单点修改: $o(logN)$
区间求和：$o(logN$)

基础模板

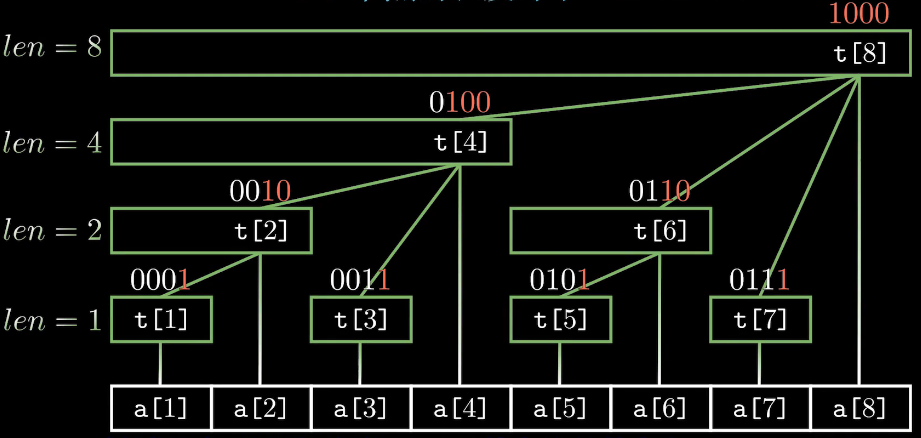
lowbit()运算：非负整数x在二进制表示下最低位1及其后面的0构成的数值

int lowbit(int x)
{
    return x & -x;
}

单点修改：在x的位置上加k

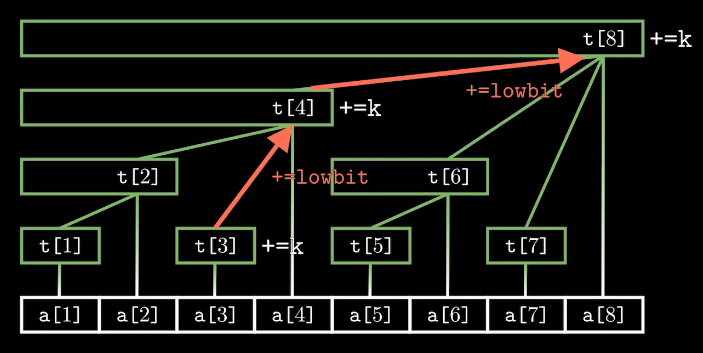
void add(int x, int k) 
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += k;
}

区间求和：求1~x区间和，即前x项和

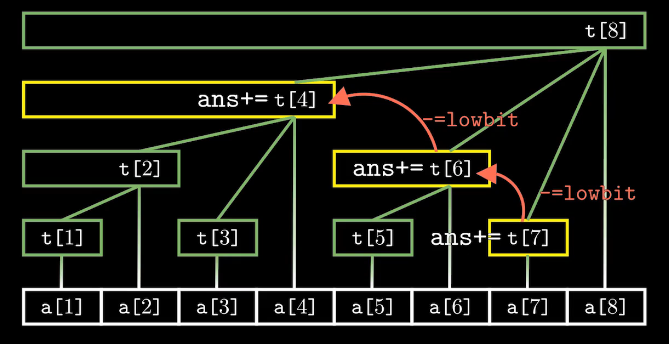
int sum(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i))
        res += t[i];
    return res;
}

解决问题

1. 多次单点修改，多次求区间和

例题
LeetCode307. 区域和检索 - 数组可修改

给你一个数组 nums ，请你完成两类查询。
1. 其中一类查询要求 更新 数组 nums 下标对应的值
2. 另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right

直接套用基础模板

class NumArray {
public:
    int tr[30010];
    int n;
    vector<int> nums;

    int lowbit(int x){
        return x&-x;
    }

    void add(int x,int c){
        for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
    }

    int sum(int x){
        int res = 0;
        for (int i = x; i; i -= lowbit(i)) res += tr[i];        
        return res;
    }

    NumArray(vector<int>& s) {
        n=s.size();
        memset(tr,0,sizeof tr);
        for(int i=0;i<n;i++) {
            add(i+1,s[i]);
            nums.push_back(s[i]);
        }
    }

    void update(int index, int val) {
        int sub=val-nums[index];
        nums[index]=val;
        add(index+1,sub);
    }

    int sumRange(int left, int right) {
        return sum(right+1)-sum(left);
    }

};

2. 多次修改区间值，多次求单点

例题
AcWing242. 一个简单的整数问题

关键：将tr[]数组变为差分数组

#include<bits/stdc++.h>
using namespace std;

const int N=100010;
int n,m;
int a[N];
typedef long long LL;//可能爆int，用long long
LL tr[N];
/////////////////////////////////////////基础模板/////////////////////////////////////////////////
int lowbit(int x){
    return x&-x;
}

void add(int x,int c){
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}

LL sum(int x){
    LL res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}
/////////////////////////////////////////基础模板/////////////////////////////////////////////////
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);

    //初始化构建差分数组
    for(int i=1;i<=n;i++) add(i,a[i]-a[i-1]);

    while(m--){
        char op[2];
        int l,r,d;
        scanf("%s",&op);
        if(*op=='C'){
            scanf("%d%d%d",&l,&r,&d);
            //关键：对差分数组的修改：l点 +c，r+1点 -c
            add(l,d);
            add(r+1,-d);
        }
        else{
            scanf("%d",&l);
            printf("%lld\n",sum(l));
        }
    }
    return 0;
}

3. 多次修改区间值，多次求区间和

例题
AcWing243. 一个简单的整数问题2

关键：引入俩个差分数组tr1[]和tr2[]，计算前缀和
tr1[]：记录正常的差分数组
tr2[]：记录i*tr1[i] (i~n) —— i倍的正常差分数组

修改后的模板

int lowbit(int x){
    return x&-x;
}

void add(int tr[],int x,int d){
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=d;
}

int sum(int tr[],int x){
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}

计算前缀和

int prefix_sum(int x){
    return (x+1)*sum(tr1,x)-sum(tr2,x);
}

实现代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;
typedef long long LL;

int n,m;
int a[N];
LL tr1[N],tr2[N];

int lowbit(int x){
    return x&-x;
}

void add(LL tr[],int x,LL d){
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=d;
}

LL sum(LL tr[],int x){
    LL res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}

LL prefix_sum(int x){
    return (x+1)*sum(tr1,x)-sum(tr2,x);
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++){
        int sub=a[i]-a[i-1];
        add(tr1,i,sub);
        add(tr2,i,(LL)sub*i);
    }

    while(m--){
        char op[2];
        int l,r;
        cin>>op>>l>>r;
        if(*op=='Q'){
            LL res=prefix_sum(r)-prefix_sum(l-1);
            cout<<res<<endl;
        }else{
            LL d;
            cin>>d;
            add(tr1,l,d);
            add(tr1,r+1,-d);
            add(tr2,l,d*l);
            add(tr2,r+1,(-d)*(r+1));
        }
    }
    return 0;
}