Floyd深度解析及其应用
因为AcWing 分享没有目录页面跳转功能 所以对页面跳转我们进行了手动跳转
一. 概念
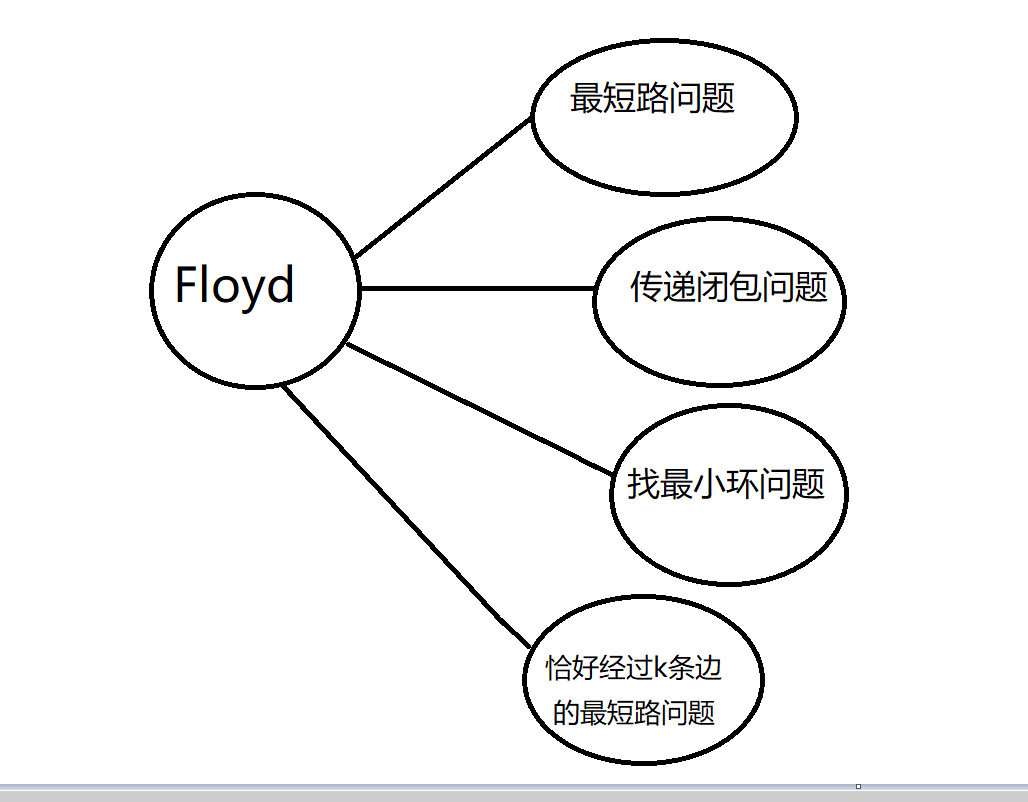
Floyd算法 是解决任意两点间的最短路径的一种算法 是一种插点算法 可以正确处理有向图或带负权非回路的最短路径算法 同时也被用于计算有向图的传递闭包 Floyd时间复杂度为($N^3$) 空间复杂度为O($N^2$)
二. 算法证明
$\space\space$Floyd算法
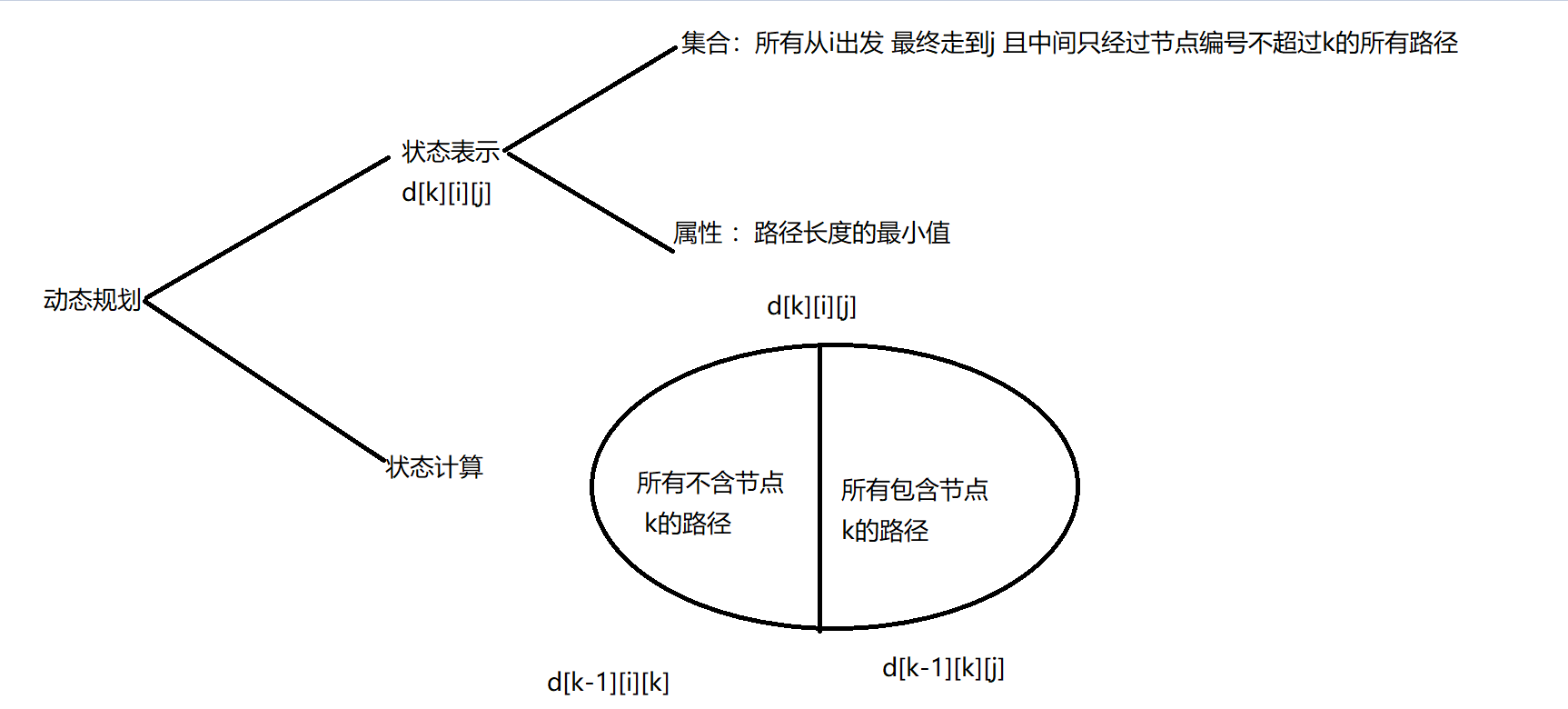
本质是个区间DP问题
状态表示 : f[k][i][j]表示 所有从i出发 最终走到j 且只经过节点编号不超过k的所有路径的最小值
阶段划分 : 节点编号k的不同
转移方程 : f[k][i][j] = min(f[k][i][j], f[k - 1][i][k] + f[k - 1][k][j])
通过DP背包思想 我们约掉了第一维 进而表示Floyd
$\space\space$算法模板
void floyd()
{
for(int k = 1; k <= n; k ++)
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
特别注解
$\space\space$DP问题中 第一维往往是枚举阶段内容 即该述中的”阶段划分:节点编号k的不同”
三. 算法用途


写的真不错,博主我要盗到我的笔记中喽。
图画的好像也有点问题~而且可以去掉第一维也不是因为背包思想,而是因为f[k - 1][i][k] + f[k - 1][k][j]这个状态的f[k - 1][i][k]和f[k - 1][k][j]本身就是到达k或从k出发,中间再经过k肯定不会更优,所以f[k - 1][i][k]和f[k - 1][k][j]本身就是f[k][i][k]和f[k][k][j]的最优状态,所以可以省去第一维。这个是我自己的理解,不是很严谨,严格的证明可以去看看OI-WIKI。
状态转移方程写错了吧,应该是f[k][i][j] = min(f[k-1][i][j], f[k - 1][i][k] + f[k - 1][k][j]),其中f[k-1][i][j]是不经过节点k的状态,f[k - 1][i][k] + f[k - 1][k][j]是经过节点k的状态。
写得不错,可以挂个链接不?我想推荐一下
感谢巨巨的解析orz
一直以为floyd只有最短路的功能,自信满满的去做提高课的题,才发现自己连题解都看不懂。
哈哈 加油
求关注
既然你诚心诚意的请求了 那我就大发慈悲的满足你把 (dog
%%%%
大佬呀