解决问题：给定字符串s ,求子串p的位置

借用题解↓
1、A[ ]是模式串，即比较长的字符串。
2、B[ ]是模板串，即比较短的字符串。（可能不严谨。。。）
3、“非平凡前缀”：指除了最后一个字符以外，一个字符串的全部头部组合。
4、“非平凡后缀”：指除了第一个字符以外，一个字符串的全部尾部组合。（后面会有例子，均简称为前/后缀）
例如字符串aaabbbaa
前缀集合是{a,aa,aaa,aaab,aaabb,aaabbb,aaabbba}
后缀集合是{a,aa,baa,bbaa,bbbaa,abbbaa,aabbbaa}
最长共有元素长度2,即aa

5、“部分匹配值”：前缀和后缀的最长共有元素的长度。
6、next[ ]是“部分匹配值表”，即next数组，它存储的是每一个下标对应的“部分匹配值”，是KMP算法的核心。（后面作详细讲解）。

核心思想：在每次失配时，不是把B串往后移一位，而是把B串往后移动至下一次可以和前面部分匹配的位置，这样就可以跳过大多数的失配步骤。而每次B串移动的步数就是通过查找next[ ]数组确定的。

next数组含义

对next[j] ，是B[1,j]串中前缀和后缀相同的最大长度（部分匹配值），即 B[1,next[j]] =B[j-next[j]+1,j]。

推导过程

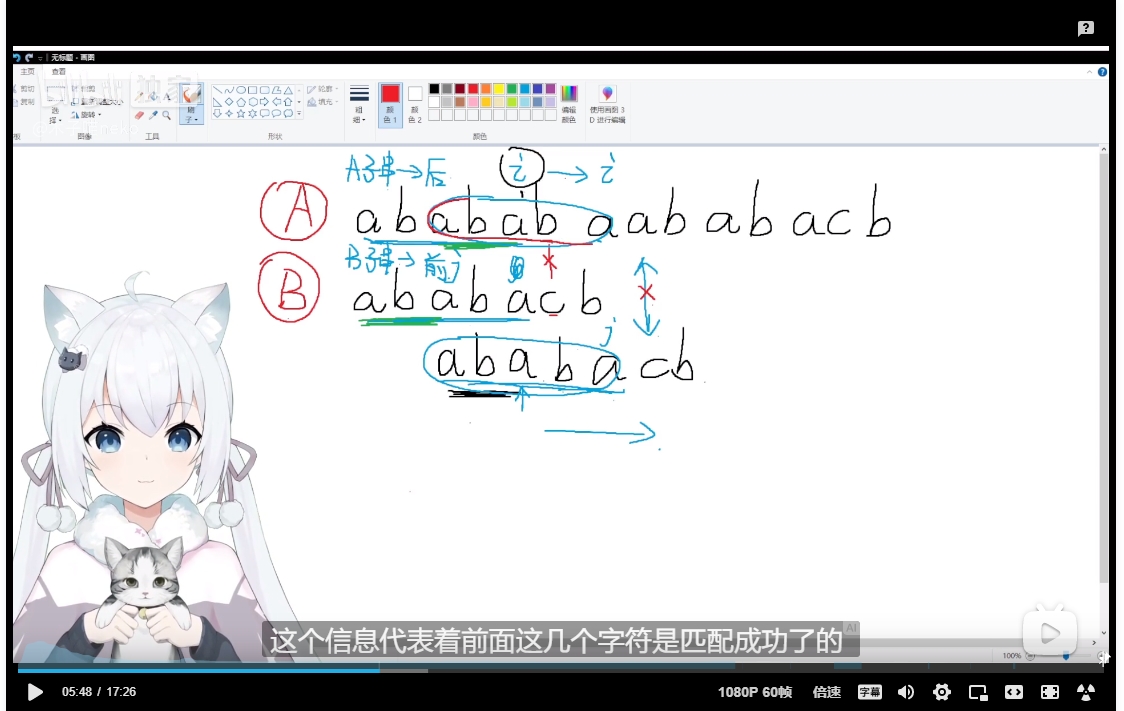
那么，A子串和B子串相同

也就是B子串前缀集合和后缀集合的交集

求next的过程

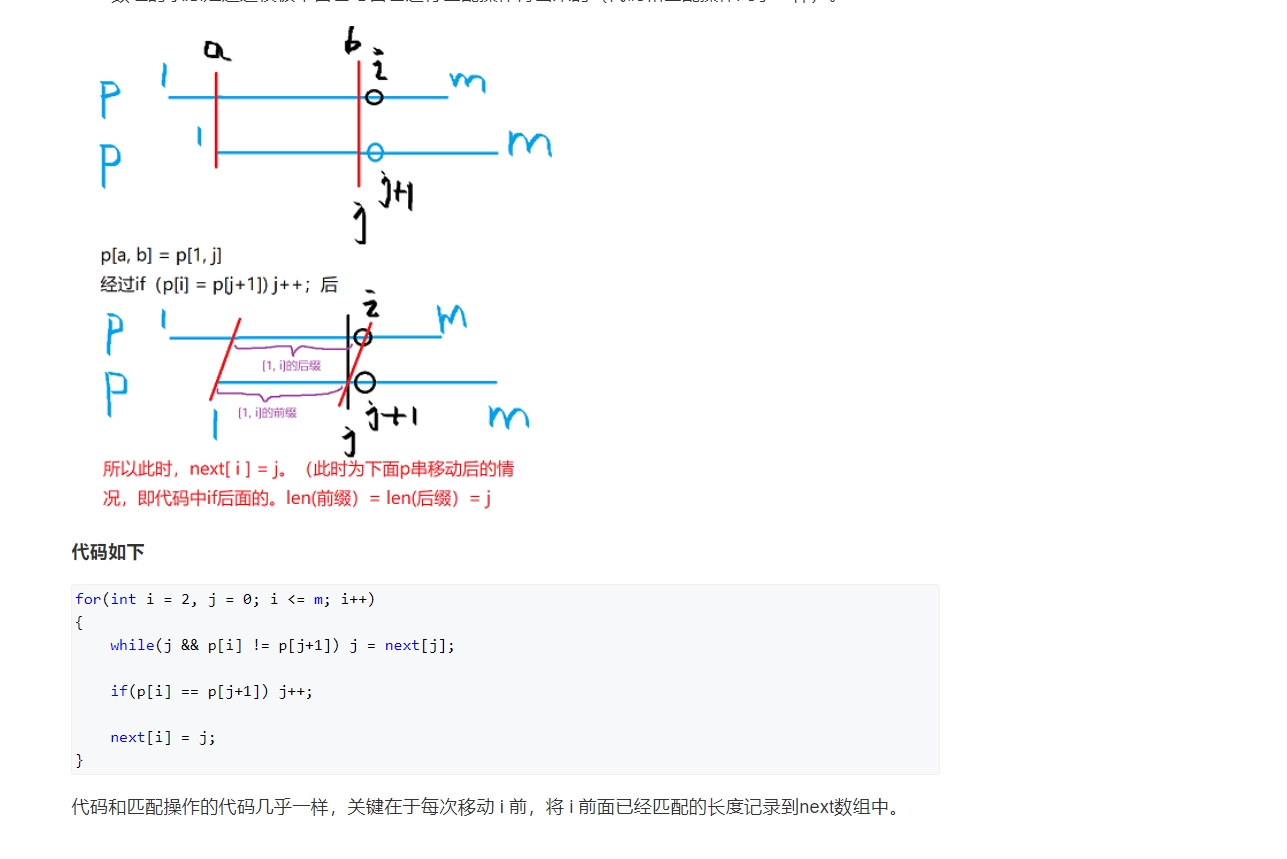
代码

#include <iostream> //kmp字符串

using namespace std;

const int N = 1e5 + 5, M = 1e6 + 5; //模板串，模式串长度

int n, m;
int ne[N]; // next数组,ne[i]记录p串前i个数前缀后缀最大公共长度
char A[M], B[N];

int main()
{
    cin >> n >> B + 1 >> m >> A + 1; //下标从1开始

    for (int i = 2, j = 0; i <= n; i++)
    {
        while (j && B[i] != B[j + 1])
            j = ne[j];
        if (B[i] == B[j + 1])
            j++;
        ne[i] = j;
    } //求next数组

    for (int i = 1, j = 0; i <= m; i++)
    {
        while (j && A[i] != B[j + 1])
            j = ne[j];
        if (A[i] == B[j + 1])
            j++;
        if (j == n)
        {
            printf("%d ", i - n);
            j = ne[j];
        }
    }

    return 0;
}

B站关注@木子喵neko,算法Vup真的太棒力