学习提高课斜率优化DP的时候了解到了凸包这个东东，然后学习了Graham算法求凸包，时间复杂度为$O(n * log_{2}^{n})$,做个整理，方便以后看。

Graham扫描算法

1. 取当前的所有点集中最下面的点a，如果有和a点在同一y轴方向上的，则选取这些点中最左边的点作为坐标原点。
   

2. 连接该点和剩余的所有的点，按照形成直线与y轴的夹角从小到大进行排序，如果角度相同，则靠前的节点排在前面。
   

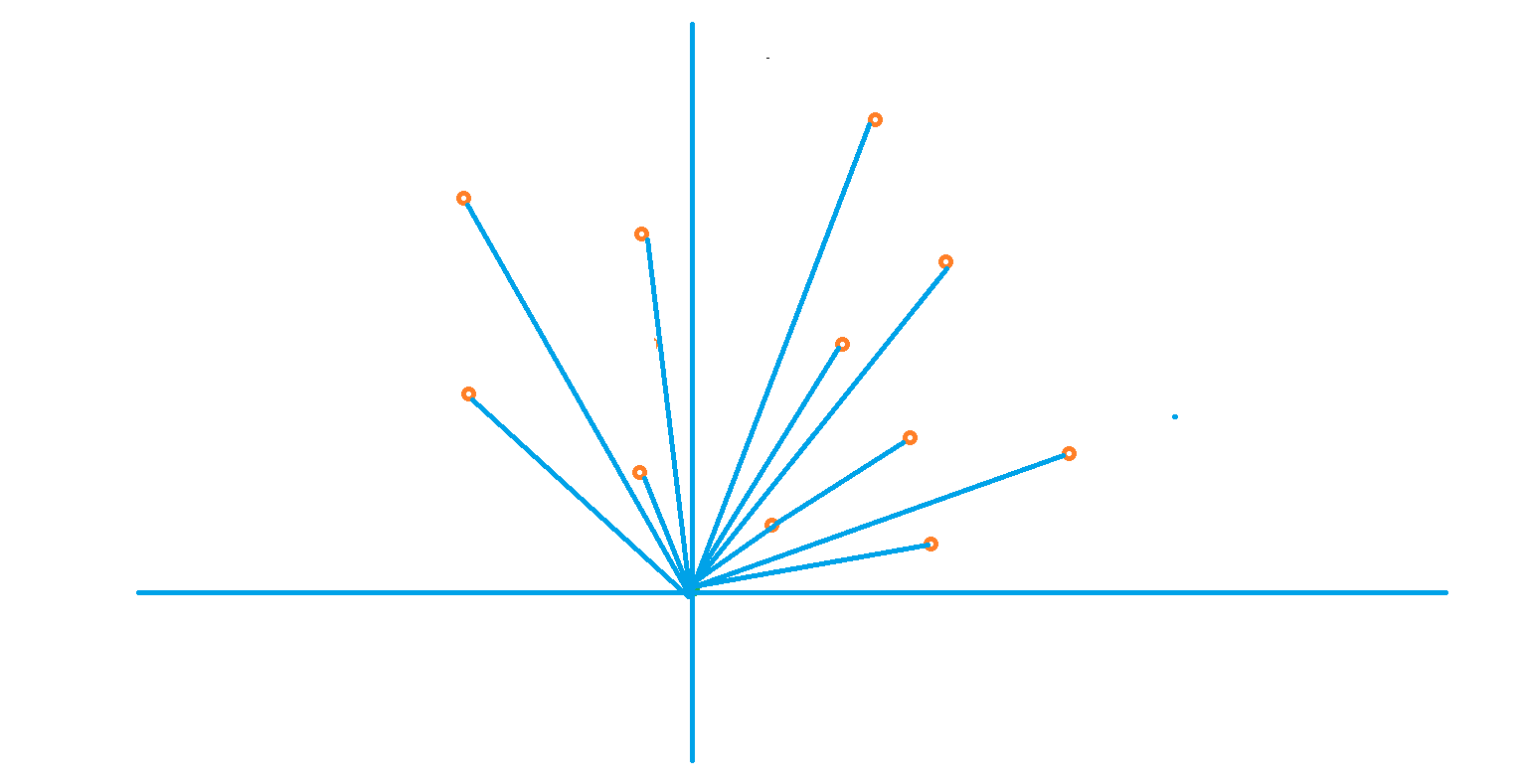
3. 使用一个队列，先将前两个点放入队列中，之后如果当前点与队尾的前一个元素b形成的直线在队尾元素a与b形成的直线的左边，则将队尾元素出队，这样循环一遍，就可以得到一个凸包。
   

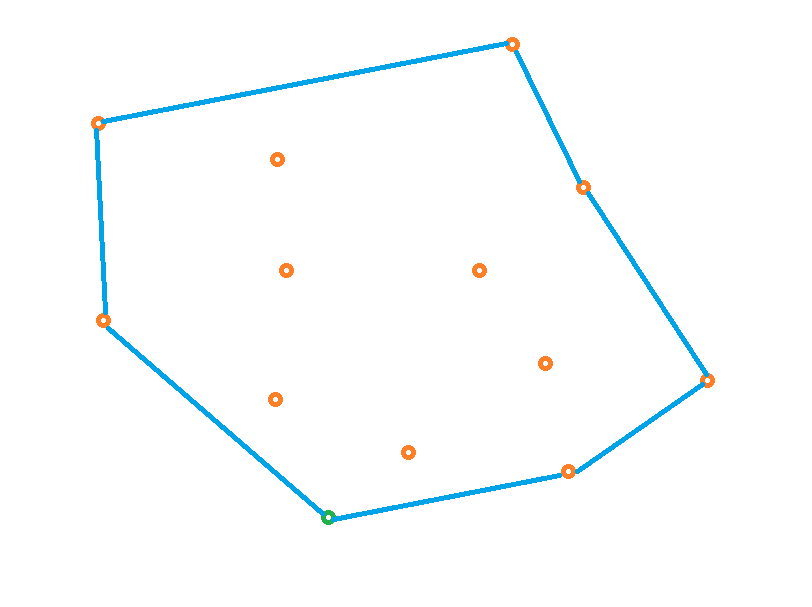
具体的代码如下：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010; 

struct node{
    double x, y;
}p[N]; // 存储所有的点

// 计算向量A - > B和向量A -> C之间的叉积，若大于0，则A -> B在A -> C的右边，若小于0，则在左边，若等于0，则共线
double X(node A, node B, node C)
{
    return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);   
}

// 计算两点之间的距离 
double len(node A, node B)
{
    return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}

// 定义比较函数 
bool cmp(node A, node B)
{
    double pp = X(p[0], A, B);
    if(pp > 0) return true;
    if(pp < 0) return false;
    return len(p[0], A) < len(p[0], B);
}

int main()
{   
    int n;
    cin >> n;
    // 读入所有的点集
    for(int i=0; i<n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);

    // 选出p[0]节点作为原点
    for(int i=0; i<n; i++)
    {
        if(p[i].y < p[0].y) swap(p[0], p[i]);
        else if(p[i].y == p[0].y && p[i].x < p[0].x) swap(p[0], p[i]);
    }

    sort(p+1, p+n, cmp); // 按照与x轴的夹角对所有的直线进行排序

    p[0] = p[0];
    p[1] = p[1];
    int tt = 1;
    for(int i=2; i<n; i++)
    {
        while(tt > 0 && X(p[tt-1], p[tt], p[i]) <= 0) tt --;
        p[++ tt] = p[i];
    }

    // 此时p中存储的点就是凸包上的所有的点。

    return 0;
}

例题： Wall

解题代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
const double pi = acos(-1.0);

struct node{
    double x, y;
}p[N];

int n, tot;
double ans, l;

// 定义叉积
// 给定三个点A，B，C， 则向量A - > B和向量A - > C之间的叉积为
//(B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y) 
double X(node A, node B, node C)
{
    return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);   
}

// 定义两点之间的距离 
double len(node A, node B)
{
    return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}

// 定义比较函数 
bool cmp(node A, node B)
{
    double pp = X(p[0], A, B);
    if(pp > 0) return true;
    if(pp < 0) return false;
    return len(p[0], A) < len(p[0], B);
}

int main()
{
    int t;
    scanf("%d", &t);

    for(int cas=1; cas<=t; cas++)
    {
        if(cas!=1) printf("\n");
        scanf("%d%lf", &n, &l);
        ans = 2 * pi * l;
        for(int i=0; i<n; i++)
        {
            scanf("%lf%lf", &p[i].x, &p[i].y);
        }
        if(n == 1)
        {
            printf("%.0f\n", ans);
        }else if(n == 2)
        {
            printf("%.0f\n", ans + len(p[0], p[1]));
        }else{
            for(int i=0; i<n; i++){
                if(p[i].y < p[0].y)
                {
                    swap(p[0], p[i]);
                }else if(p[i].y == p[0].y && p[i].x < p[0].x)
                {
                    swap(p[0], p[i]);
                }
            }

            sort(p+1, p+n, cmp);

            p[0] = p[0];
            p[1] = p[1];
            tot = 1;
            for(int i=2; i<n; i++)
            {
                while(tot > 0 && X(p[tot-1], p[tot], p[i]) <= 0) tot--;
                p[++ tot] = p[i];   
            } 

            for(int i=0; i<tot; i++)
            {
                ans += len(p[i], p[i+1]);   
            }
            ans += len(p[0], p[tot]);
            printf("%.0f\n", ans);
        }
    }

    return 0;
}