一般用在将某段区间赋值的操作上

通常我们会用一个结构体去维护一个区间的一些信息,结构体通常是这样的
mutable的意思是可变的，加上后我们就可以直接在set中修改，而不需要erase掉再重新插入
还需要重载一下运算符，保证set中集合的排序的按左端点从小到大

struct node
{
    int l, r;
    mutable int v;
    bool operator < (const node &t) const {
        return l < t.l;
    }
};

odt里最重要的操作split
先上模板

auto split(int x) {
    auto it = odt.lower_bound({x, 0, 0});
    if(it != odt.end() && it->l == x) {
        return it;
    }
    it --;
    int l = it->l, r = it->r, v = it->v;
    odt.erase(it);
    odt.insert({l, x-1, v});
    return odt.insert({x, r, v}).first;
}

我们先再set中二分查找左端点大于等于x的位置，如果找到的位置的左端点恰好等于x，那么我们直接返回
否则我们将迭代器前移一个位置，我们的目标位置就在前一个区间内，然后我们把前一个区间抹去
再插入{1, x-1, v}和{x, r, v}，这样我们就把含有x的区间拆开了
这就让我们可以做到： 任何对于[L,R]的区间操作，都可以转换成 set 上[split(L),split(R+1)]的操作了

接下来就是区间赋值操作

void assign(ll l, ll r, ll v) {
    auto end = split(r + 1), begin = split(l); // 顺序不能颠倒
    tree.erase(begin, end); 
    tree.insert(node(l, r, v)); 
}

看图
假设我们当前已经维护出了这样的三个区间

现在我们想要进行区间赋值操作，把这两个之间的部分赋值成5

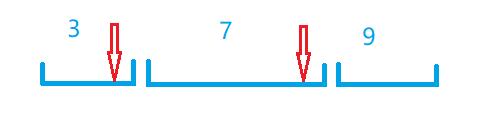
那么经过我们的split(r+1),和split(l)后区间会变成

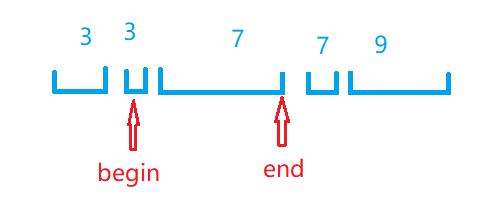
此时我们把begin到end的区间删除掉再插入{l,r,3}即可

例题（校门外的树
代码

 #include <bits/stdc++.h>

#define endl "\n"
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;

const int N = 2e5 + 10;
const int mod = 1e9 + 7;

int l, n;
int ans;
struct node
{
    int l, r;
    mutable int v;
    bool operator < (const node &t) const {
        return l < t.l;
    }
};
set<node> odt;

set<node>::iterator split(int x) {
    auto it = odt.lower_bound({x, 0, 0});
    if(it != odt.end() && it->l == x) {
        return it;
    }
    it --;
    int l = it->l, r = it->r, v = it->v;
    odt.erase(it);
    odt.insert({l, x-1, v});
    return odt.insert({x, r, v}).first;
}

void cut(int l, int r) {
    auto end = split(r+1), begin = split(l);
    for(; begin != end; begin ++) {
        if(begin->v == 2) {
            ans += (begin->r - begin->l + 1);
        }
    }
    end = split(r+1), begin = split(l);
    odt.erase(begin, end);
    odt.insert({l, r, 0});
}

void plant(int l, int r) {
    auto end = split(r+1), begin = split(l);
    for(; begin != end; begin ++) {
        if(begin->v == 0) {
            begin->v = 2;
        }
    }
}

int all(int l, int r) {
    auto end = split(r+1), begin = split(l);
    int res = 0;
    for(; begin != end; begin ++) {
        if(begin->v == 2) {
            res += (begin->r - begin->l + 1);
        }
    }
    return res;
}


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);


    cin >> l >> n;

    odt.insert({-1,l+1,1});

    while(n --) {
        int op, l, r;
        cin >> op >> l >> r;
        if(op == 0) {
            cut(l, r);
        } else {
            plant(l, r);
        }
    }

    cout << all(0, l) << endl << ans << endl;


}