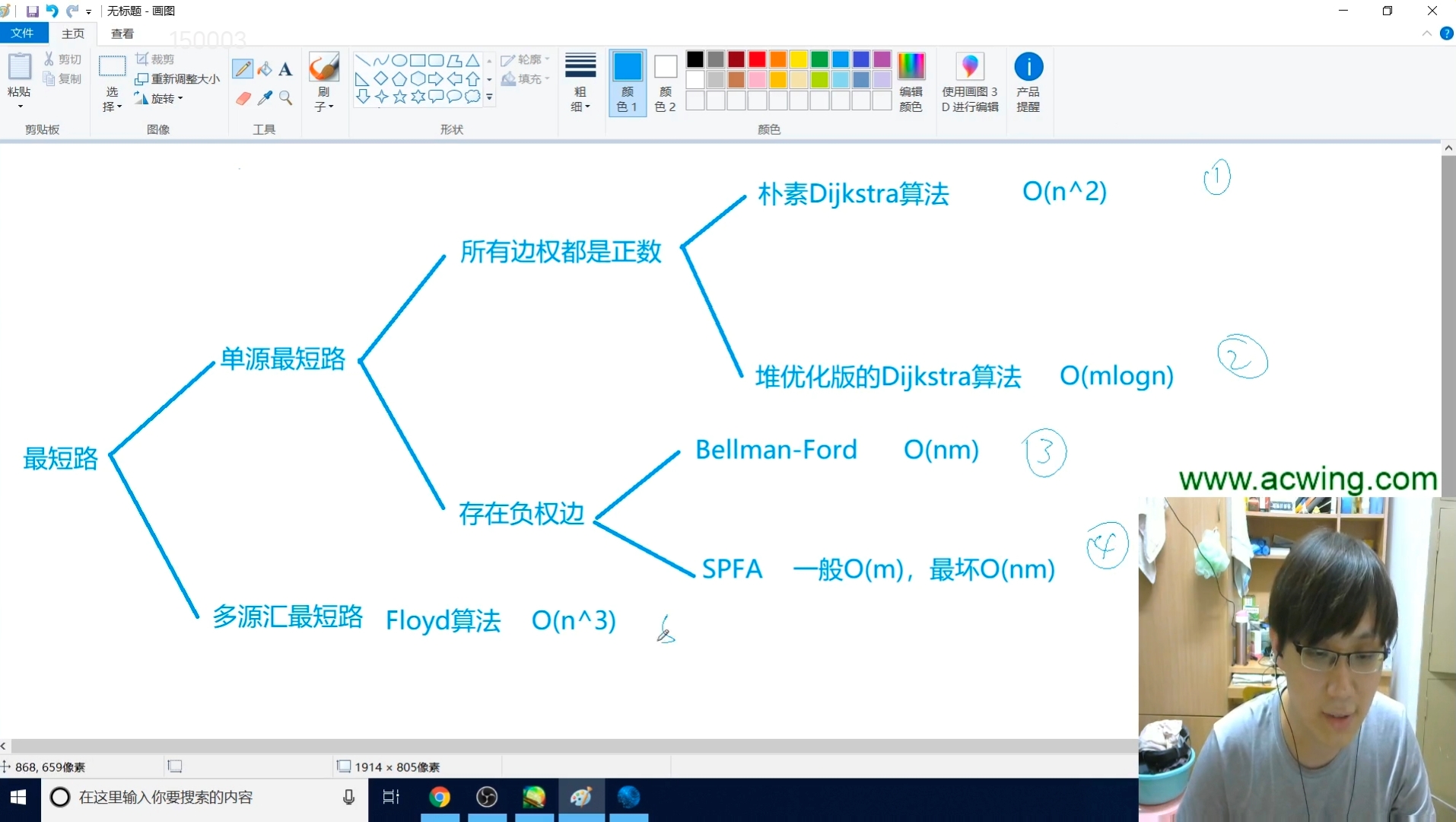
一、朴素版Dijkstra算法$O(n^2)$
算法思路:
算法重复从结点集$V-S$中选择最短路径估计最小的结点$u$,将$u$加入到集合$S$,然后对所有从$u$出发的边进行松弛操作--------《算法导论》
Dijkstra算法中要求所有边都为正权边,因为该算法每次找到的最路径的最小结点一旦被确定,则在之后的更新中都不会改变其值了,所以就造就了边的累加值一定是单调递增的,而带有负权边就会破坏该单调性!
ex:
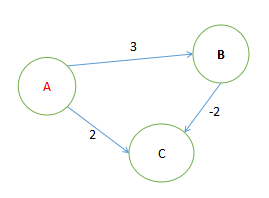
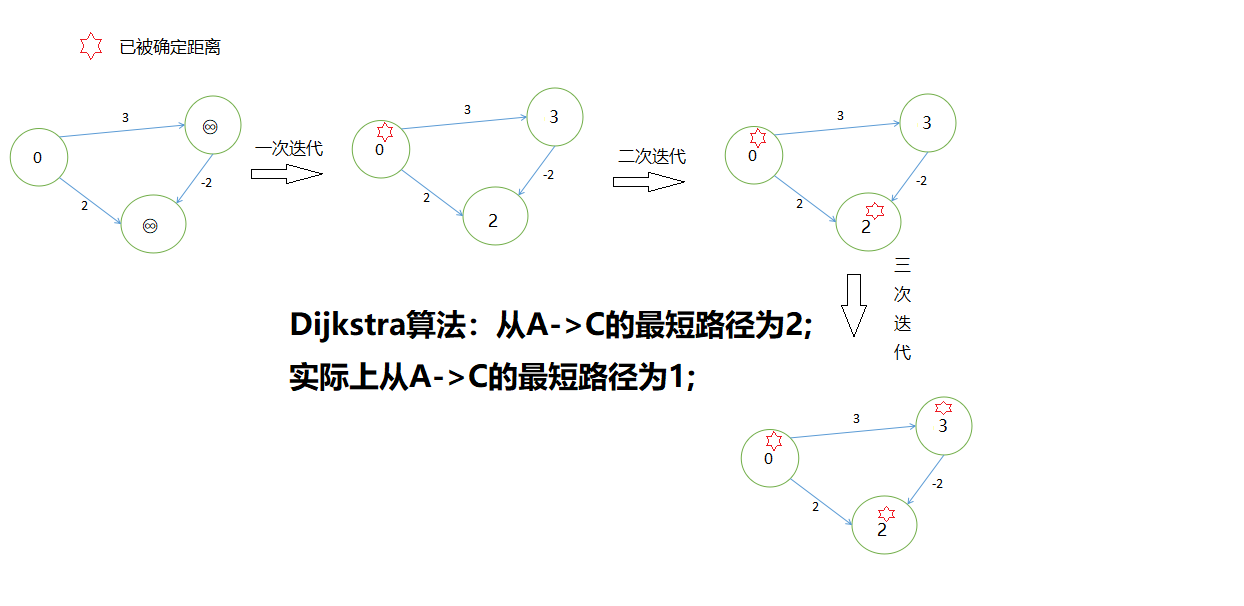
朴素版Dijkstra算法模板:—> 传送门
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int g[N][N];
int n, m;
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);//初始话所有距离为无穷大
dist[1] = 0;//起始结点的距离为0
for (int i = 0; i < n; i ++ ) //迭代n次,每一次都确定一个结点的距离
{
int t = -1;
for (int j = 1; j <= n; j ++ ) //在未确定距离的结点中,寻找距离最小的点
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;//确定了该结点的距离
for (int j = 1; j <= n; j ++ )//用该结点去更新其他结点的距离(松弛操作)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if (dist[n] == 0x3f3f3f3f) return -1;//如果n结点的距离还是无穷大时,则证明不能从1->n
return dist[n];
}
int main()
{
cin >> n >> m;
memset(g, 0x3f, sizeof g);//初始化为无穷大
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
if (a == b) continue;
g[a][b] = min(g[a][b], c);//如果有重边的话,则取最小的边
}
printf("%d", dijkstra());
return 0;
}
二、堆优化版Dijkstra算法$O(mlogn)$
算法思路:
使用小根堆来确定最小距离的结点--------《y总语录》
堆优化版Dijkstra算法模板:—> 题目传送门
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 15e4 + 10;
int h[N], ne[N], e[N], w[N], idx;//邻接表三件套
int dist[N];
PII heap[N];//堆
int cnt;
int n, m;
bool st[N];
void add(int a, int b, int c)//数组模拟链表插入操作
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx ++ ;
}
void down(int x)//堆的下落操作(不懂的复习一下堆的操作)
{
int t = x;
if (x * 2 <= cnt && heap[x * 2] < heap[t]) t = x * 2;
if (x * 2 + 1 <= cnt && heap[x * 2 + 1] < heap[t]) t = x * 2 + 1;
if (t != x)
{
swap(heap[x], heap[t]);
down(t);
}
}
void up(int x)//堆的上升操作
{
while (x / 2 > 0 && heap[x / 2] > heap[x])
{
swap(heap[x], heap[x / 2]);
x /= 2;
}
}
void push(PII x)//堆的push操作
{
heap[ ++ cnt] = x;
up(cnt);
}
void pop()//堆的pop操作
{
heap[1] = heap[cnt -- ];
down(1);
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);//初始化所有结点距离为无穷大
dist[1] = 0;
push({0, 1});//1结点入堆
while (cnt != 0)//当堆为空时算法结束
{
auto t = heap[1];//取出小根堆顶端元素,并出堆
pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;//如果ver这个结点被确定过,则继续取出下一个顶端元素
st[ver] = true;//ver这个结点被确定距离
for (int i = h[ver]; i != -1; i = ne[i])//用该结点去更新其他结点
{
int j = e[i];
if (dist[j] > distance + w[i])//松弛操作
{
dist[j] = distance + w[i];
push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;//如果n结点的距离仍然没有确定,则不能从1->n,无最短路
return dist[n];//返回最短路
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);//初始化
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
if (a == b) continue;
add(a, b, c);
}
printf("%d", dijkstra());
return 0;
}
三、Bellman-Ford算法$O(nm)$
算法思路:
Bellman-Ford算法通过对边的进行松弛操作来渐进地降低从源结点$s$到每个结点$v$的最短路径的估计值$v,d$,直到该估计值与实际路径权重$\delta(s,v)$相同为止--------《算法导论》
ex:
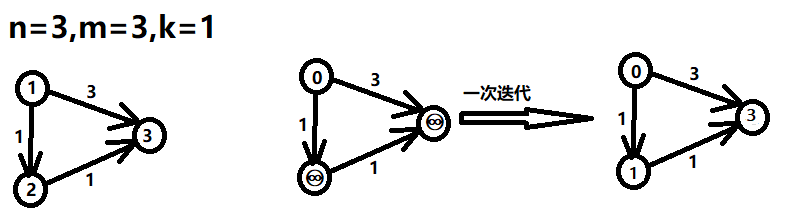
Bellman-Ford算法模板:—> 题目传送门
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510, M = 1e4 + 10;
int n, m, k;
int dist[N], backup[N];
struct Edge//所有边的集合
{
int a, b, w;
} edges[M];
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);//所有结点的距离都设置为无穷大
dist[1] = 0;
for (int i = 0; i < k; i ++ )//最多进行k步
{
memcpy(backup, dist, sizeof dist);//因为要的是上一次迭代的dist所以要拷贝一个backup数组
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w);//松弛操作
}
}
return dist[n];
}
int main()
{
cin >> n >> m >> k;
for (int i = 0; i < m; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
edges[i] = {a, b, w};
}
int t = bellman_ford();
if (t > 0x3f3f3f3f / 2) puts("impossible");//如果dist[n]不存在则无法以k步从1->n
else printf("%d", dist[n]);//输出答案
return 0;
}
四、spfa算法$O(m)$
算法思路:
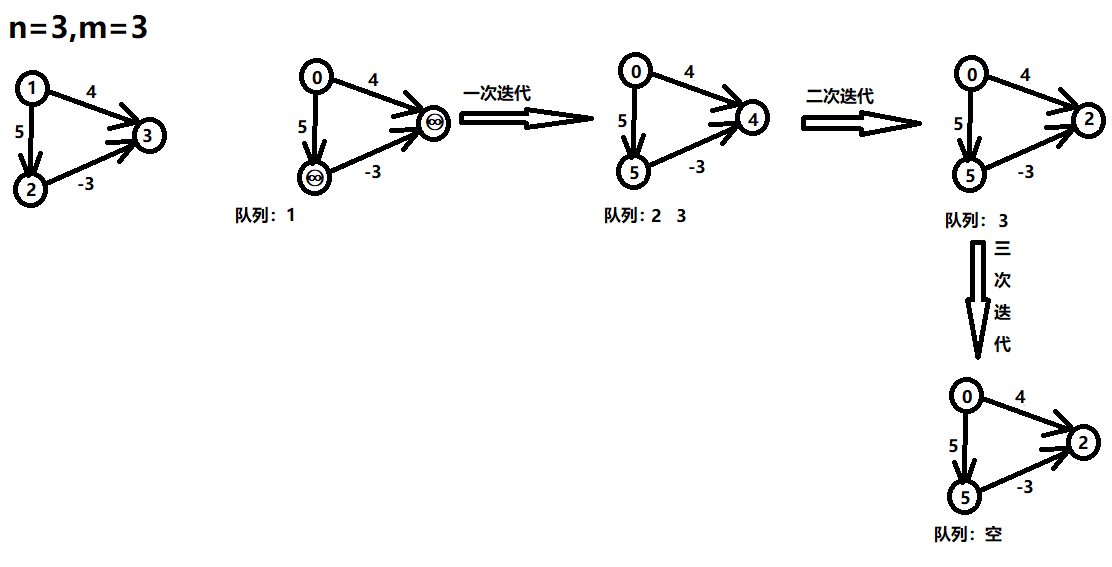
设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点$u$,并且用$u$点当前的最短路径估计值对离开$u$点所指向的结点v进行松弛操作,如果$v$点的最短路径估计值有所调整,且$v$点不在当前的队列中,就将$v$点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
--------《百度百科》
证明算法的正确性:
每次将点放入队尾,都是经过松弛操作达到的。换言之,每次的优化将会有某个点$v$的最短路径估计值$d[v]$变小。所以算法的执行会使$d$越来越小。由于我们假定图中不存在负权回路,所以每个结点都有最短路径值。因此,算法不会无限执行下去,随着$d$值的逐渐变小,直到到达最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。--------《百度百科》
ex:
SPFA算法模板:—> 题目传送门
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int h[N], ne[N], e[N], w[N], idx;//邻接表全家桶
int dist[N];
int q[N];//队列
int n, m;
bool st[N];
void add(int a, int b, int c)//构建邻接表
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx ++ ;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);//初始化距离全为无穷大
dist[1] = 0;
q[0] = 1;
st[1] = true;//在队列中的点为true,不在为false
int hh = 0, tt = 0;
while (hh <= tt)
{
int t = q[hh ++ ];//出队列
st[t] = false;//t结点解除禁锢
for (int i = h[t]; i != -1; i = ne[i])//遍历t结点的邻接结点
{
int j = e[i];
if (dist[j] > dist[t] + w[i])//如果可以进行松弛操作则松弛
{
dist[j] = dist[t] + w[i];
if (!st[j])//若该结点不在队列中则加进队列中去
{
q[ ++ tt] = j;
st[j] = true;
}
}
}
}
return dist[n];
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);//对头结点进行初始化操作
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
if (a == b) continue;
add(a, b, c);
}
int t = spfa();
if (t > 0x3f3f3f3f / 2) puts("impossible");
else printf("%d", dist[n]);
return 0;
}
五、Floyd算法$O(n^3)$
算法思路:
- 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
- 对于每一对顶点 $u$ 和 $v$,看看是否存在一个顶点 $w$ 使得从 $u$ 到 $w$ 再到 $v$ 比已知的路径更短。如果是更新它。
--------《百度百科》
Floyed算法模板:—> 题目传送门
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 210, INF = 1e9;
int n, m, q;
int g[N][N];
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
int main()
{
cin >> n >> m >> q;
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= n; j ++ )
if(i == j) g[i][j] = 0;
else g[i][j] = INF;
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
floyd();
while (q -- )
{
int a, b;
cin >> a >> b;
if (g[a][b] > 0x3f3f3f3f / 2) puts("impossible");
else printf("%d\n", g[a][b]);
}
return 0;
}


写的啥玩意
jj给你割了,小秋子