笔记汇总

网络流的定义

以下内容如无特殊说明，均不考虑 反向边

可行流与最大流

给出一个有向图 $G = (V, E)$，图中有 一源点 和 一汇点，

对于其中任意一条边 $(u, v) \in E$ 都有一个 容量限制 $c(u, v)$（其可行流 $f(u, v) <= c(u, v)$）

整个网络里除了 源点 和 汇点 之外，其余点 不存储容量，即流入的流量等于流出的流量（流量守恒）

但是如果 容量限制 $c(u, v) < f(u, v)$，则大于 $c(u, v)$ 的部分不被计算。

可行流的流量 $=$ 从源点流出的流量 $-$ 流入源点的流量 (一般来说不会出现 回流源点 的情况)

、

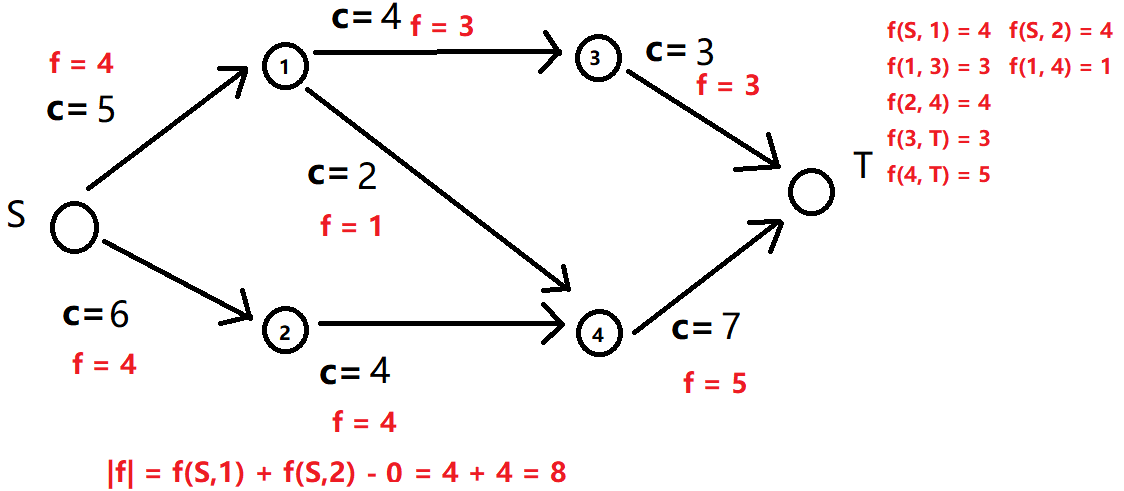值得注意的是，一条可行流并不意味着要将 容量限制 拉满，但是要确保之后不会溢出。

最大流即为 最大可行流，如上图的最大流为 $9$

残留网络 $G_f$

对于一个残留网络 $G_f = (V_f, E_f)$ 有：$V_f = V, E_f = E + E 的反向边$