字符串哈希

一、字符串哈希简介

哈希表用于快速地存储和查询数据，而数据类型是多样的。
当 数据类型为字符 时，就可以使用字符串哈希。

当然，直接 存储一个很长的字符串需要 大量空间，
在本模板中，会将每个字符串 转换为相应的数值 。

哈希表回顾：模拟哈希表 - AcWing

二、应用场景 —— 字符串哈希

给定一个长度为 n 的字符串，
判断该字符串 两个区间 [ l1 , r1 ] 、[ l2 , r2 ] 所包含的字符串 子串 是否完全相同。

题源 ： 841. 字符串哈希 - AcWing题库

解题思路：
在哈希表中，要查找一个元素，能通过 哈希函数 计算出其对应的 哈希值，直接查询。
在理想的情况下，元素与其哈希值 一 一对应。

在字符串哈希中，对于给定的字符串 ( 子串 ) ，也能求出其对应的哈希值。

若两个字符串 ( 子串 ) 的 哈希值完全相同，则就能断定两个字符串 ( 子串 ) 完全相同。

三、字符串哈希具体实现

1. 原理解析：

字符串 哈希函数 的 核心 是用 进制数 的角度，把一个字符串看成是一个 p 进制的数字。
$$ \begin{array}{l} \;\;十进制数 : 54321\;\;{\rm{ = }}\;\;5\;*{10^4} + 4\;\*{10^3} + 3\;\*{10^2} + 2\;\*{10^1} + 1\;\*{10^0}\\\\ \;\;二进制数 : 10101\;\;{\rm{ = }}\;\;1\;\*{2^4} + 0\;\*{2^3} + 1\;\*{2^2} + 0\;\*{2^1} + 1\;\*{2^0}\\\\ {\rm{\;\;p\;进制数 :}}\;{\rm{abcde}}\;\;{\rm{ = }}\;\;{\rm{a}}\; \*{p^4} + b\;\*{p^3} + c\;\*{p^2} + d\;\*{p^1} + e\;\*{p^0} \end{array} $$
说明：每个字符有其唯一对应的 ASCII 码 ，因此在确定了 p 的取值后，能将字符串转换为数值。

存在疑问：数学中的进制数均有其 特有的性质

如 10 进制数 由数字 0/1/2/3/4/5/6/7/8/9 组成；
2 进制数 由数字 0/1 组成。

但 p 进制数 呢？这让算法看似难以理解。

实际上，我们只是借用了进制数的 展开式 这一 形式 ，作为 哈希函数。
其 目的 只是通过一种 计算规则 ( 映射方式 ) ，将一个字符串转换为 唯一 对应的数值 。
而不是将字符串真的作为 p 进制数。

2. 字符串哈希定义

const int N = 100010;
const int P = 131; // 将字符串看成 P 进制的数，而这个 ( 大写 ) P 的值是自己定的 

int h[N]; // 存储字符串每个前缀的哈希值 
int p[N]; // 存储展开式中的权值 ( p^0, p^1 , p^2, p^3 ... ) ( 小写 p )
char str[N]; // 存储字符串

说明：P 的取值在之后解释。（ 大小写不要混淆 ）

3. 字符串 前缀 哈希值的计算

字符串前缀：是指字符串的任意首部。

举例：字符串 "abcd" 的前缀有 "a" 、"ab" 、"abc" 、"abcd"

$$ \begin{array}{l} \;\;\;\;\;{\kern 1pt} h[a]\;\; = \;\;a\;\*{p^0}\\\\ \;\;\;\,h[ab]\;\; = \;\;a\;\*{p^1} + b\;\*{p^0}\;\; = {\kern 1pt} \;\;h[a]\;\*p + h[b]\\\\ \;\;h[abc]\;\; = \;\;a\;\*{p^2} + b\;\*{p^1} + c\;\*{p^0}\;\; = {\kern 1pt} \;\;h[ab]\;\*p + h[c]\\\\ h[abcd]\;\; = \;\;a\;\*{p^3} + b\;\*{p^2} + c\;\*{p^1} + d\;\*{p^0}\;\; = {\kern 1pt} \;\;h[abc]\;\*p + h[d] \end{array} $$

int n; // 输入的字符串的长度
scanf( "%d%s", &n, str + 1 ); // 题目要求字符串的位置从 1 开始编号 ( str + 1 )

p[0] = 1; // p^0 == 1
// h[0] == 0 ( 保持默认值即可 )，这样不会影响 h[1] 的计算
// h[1] = h[0]*p + '1' = '1'( 1 为对应的字符 )

for( int i = 1; i <= n; i++ )
{
    h[i] = h[i - 1] * P + str[i]; // 计算字符串每个 前缀 的哈希值 
    p[i] = p[i - 1] * P; // 计算展开式中的各个权值 ( p^0, p^1 , p^2, p^3 ... ) 
}

说明：

1. scanf( "%s", str + 1 ); 表示字符串是从 str[1] 开始存储的
   即 str[1] 是第 1 个字符， str[2] 是第 2 个字符。

2. 对于字符串 abc ，h[1] == h[a] 、h[2] == h[ab]
   由此，对于一个字符串 x ，唯一对应了哈希值 h[x]

3. p[x] == p^x

4. 计算字符串前缀的哈希值的 作用：
   可以利用前缀哈希值算出任意一个 子串的哈希值 。

4. 子串哈希值

( 1 ) 子串哈希值的原理

首先类比真正的进制数 ( 以十进制为例 )

对于十进制数 987654321 ，第 1 个数为 9 ，第 2 个数为 8
要求取得区间 [ 4 , 6 ] 上的数。

从人的角度，一眼就能知道这个数 ( 子串 ) 为： 654（ 六百五十四 ）
而想要得到这个数，更严谨的做法是去掉 子串 987654 前面的 子串 987。

但计算上怎么处理呢？

若直接相减 987654 - 987 == 986667 != 654
其原因在于其中的 权重：987 不是表面的 九百八十七 ，而是 九十八万七千 。
正确的计算方法：987654 - 987000 == 654

从展开式我们能更清楚地区分：

$$ \begin{array}{*{20}{l}} {987654\;\;{\rm{ = }}\;\;9\;\*{{10}^5} + 8\;\*{{10}^4} + 7\;\*{{10}^3} + 6\;\*{{10}^2} + 5\;\*{{10}^1} + 4\;\*{{10}^0}}\\\\ {987000\;\;{\rm{ = }}\;\;9\;\*{{10}^5} + 8\;\*{{10}^4} + 7\;\*{{10}^3}\;\;{\rm{ = }}\;\;(987)\;\*{{10}^3}}\\\\ {\quad \;\,987\;\,\,{\rm{ = }}\;\;9\;\*{{10}^2} + 8\;\*{{10}^1} + 7\;\*{{10}^0}} \end{array} $$

因此要提高 987 各个位的 权数 ，而这个权数与区间相关。
对于区间 [ 4 , 6 ] ，十进制数 要乘的权数为：10^( 6 - 4 + 1) == 10^3
即对于区间 [ l , r ]，十进制数 要乘的权数为：p^( r - l + 1 )

( 2 ) 子串哈希值的计算

综上，我们同样将这种计算方式运用到字符串哈希中
即对于区间 [ l , r ]，p 进制数 要乘的权数为：p^( r - l + 1 )

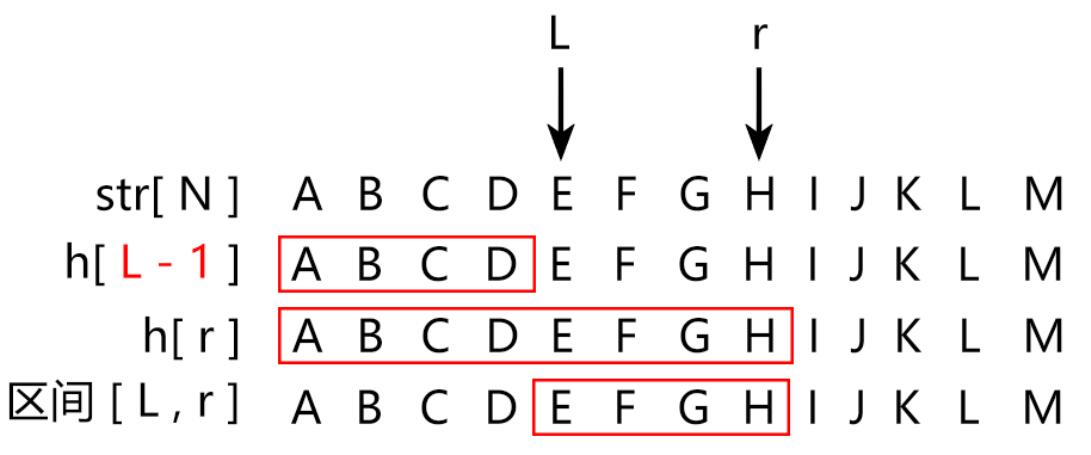
int get( int l, int r ) // 计算区间 [ l , r ] 内字符串的哈希值 
{
    return h[r] - h[ l - 1 ] * p[ r - l + 1];
}

{:height=”50%” width=”50%”}

四、补充说明 —— 字符串哈希

1. 映射需要注意

一般情况下不能将某个字母映射成 0，
若 A = 0 则 AA = 0, AAA = 0, …… 这样将不同的字符串映射成了同样的数，产生错误（冲突）

2. 字符串哈希值的大小

int 类型的数组 h[N] 中存储每个字符串的哈希值，
随着字符串长度的增加，h[x] 的值会迅速增大 ( 指数级增大 )，
很快就会 超过 int 类型的存储范围，产生错误。

在之前的 模拟哈希表 中，我们使用 取模 ( mod N ) 运算，
将一个很大范围的数，映射到了一个较小的、可以接受的区间 [ 0 , N-1 ] 中。

在字符串哈希中，我们也可以采用取模 ( mod ) 运算。
即对于每个 h[x] % Q 。这样我们就需要考虑 模数 Q 的取值。

在本模板中使用 自然溢出法 ，
不使用 int 存储哈希值，而使用 unsigned long long 类型存储，即：

unsigned long long h[N];
unsigned long long p[N];

unsigned long long 类型的范围为：[ 0 , 2^64 - 1 ] ,
若存储的数据超过其范围，则自动取模 ( mod 2^64 )，即 Q == 2^64

3. 字符串哈希中的冲突

存在疑问：按照上述的计算方式，会不会存在 不同的字符串 ( 子串 ) 对应 同样的哈希值 的情况？

理论上是存在这种冲突的，
要想减少冲突的发生，关键在于 p 进制数中 P ，以及模数 Q 的选取。

经验：当 P = 131 或 13331，Q = 2^64，在 99.99% 的情况下不会发生冲突 ( y 总说的hh )

因此不必深究。

五、函数模板 —— 字符串哈希

#include <iostream>

using namespace std;

const int N = 100010;
const int P = 131; // 将字符串看成 P 进制的数，而这个 (大写) P 的值是自己定的 

typedef unsigned long long ULL; // 本来要写三个单词，现在只要写三个字母，省代码 

ULL h[N]; // 存储字符串每个前缀的哈希值 
ULL p[N]; // 存储展开式中的权值 ( p^0, p^1 , p^2, p^3 ... ) 

ULL get( int l, int r ) // 计算区间 [ l , r ] 内字符串的哈希值 
{
    return h[r] - h[ l - 1 ] * p[ r - l + 1];
}

int main() 
{
    int n; // 输入的字符串的长度
    int m; // 输入的查询次数 
    char str[N];
    scanf( "%d%d%s", &n, &m, str + 1 ); // 题目要求字符串的位置从 1 开始编号, str + 1

    p[0] = 1; // p^0 == 1
    // h[0] == 0 ( 保持默认值即可 )，这样不会影响 h[1] 的计算
    // h[1] = h[0]*p + '1' = '1'( 1 为对应的字符 )

    for( int i = 1; i <= n; i++ )
    {
        h[i] = h[i - 1] * P + str[i]; // 计算字符串每个 前缀 的哈希值 
        p[i] = p[i - 1] * P; // 计算展开式中的各个权值 ( p^0, p^1 , p^2, p^3 ... ) 
    }

    while( m-- )
    {
        int l1, r1, l2, r2;
        scanf( "%d%d%d%d", &l1, &r1, &l2, &r2 );

        if( get( l1, r1 ) == get( l2, r2 ) ) puts("Yes"); 
        // 两个子串哈希值相等，则判断两子串 相同 
        else puts("No");
    }

    return 0;
}

六、参考资料

1. y 总的课~~
2. unsigned long long类型与long long类型 - Fzzf1 - 博客园 (cnblogs.com)

（接受批评指正，欢迎交流补充~~ XD）
（害那个 markdown 把 LaTeX 里面的乘号 * 识别成斜体让我好找）