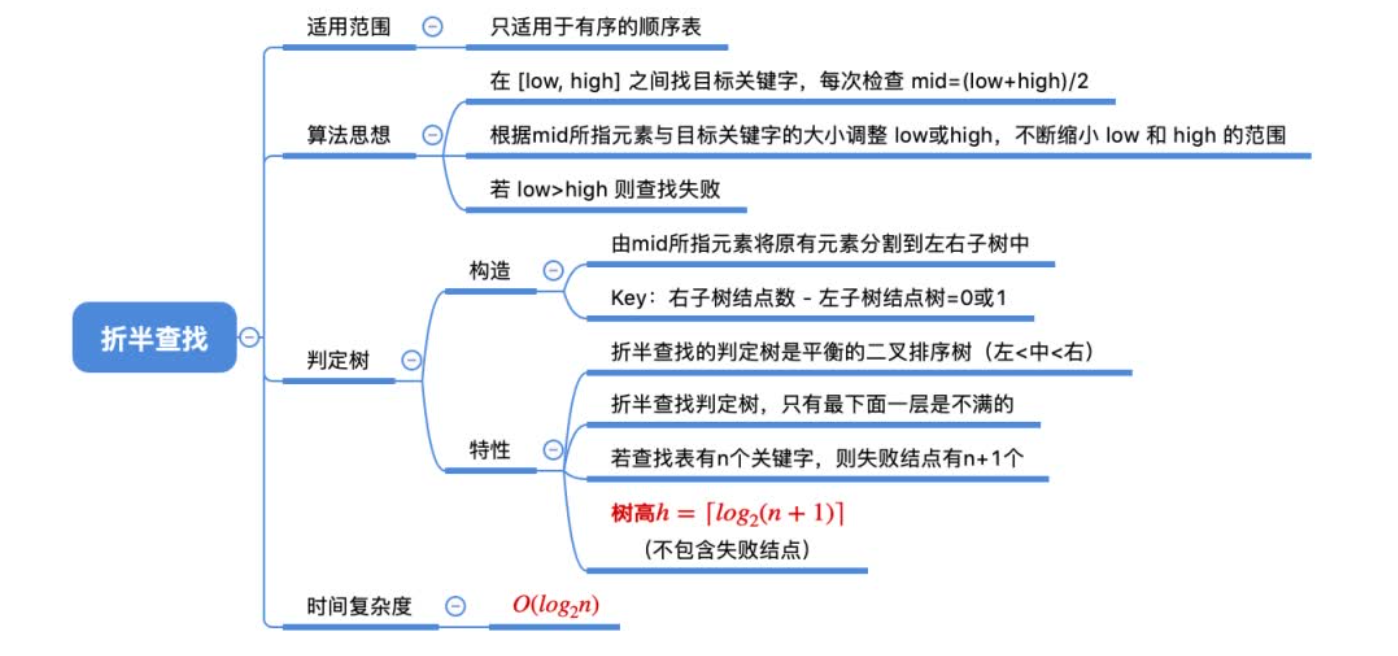
折半查找，⼜称“⼆分查找”，仅适⽤于有序的顺序表。
要求
1.必须采用顺序存储结构。
2.必须按关键字大小有序排列。

算法思想
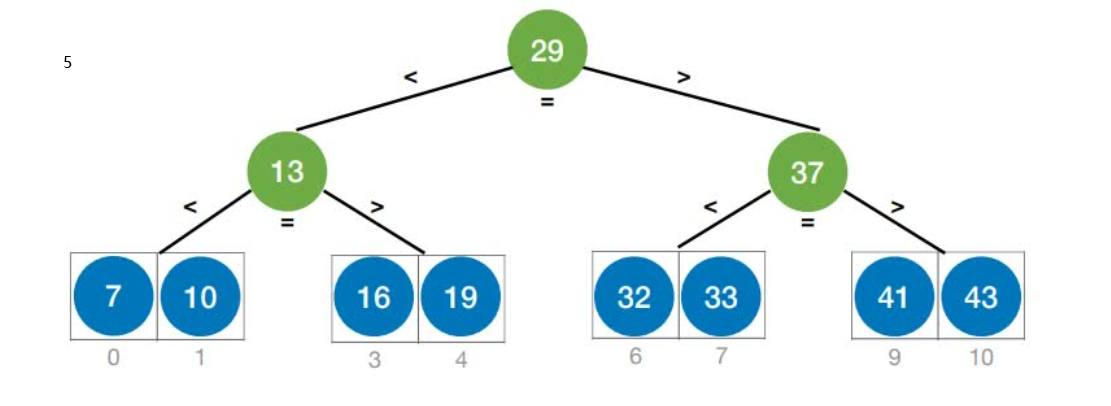
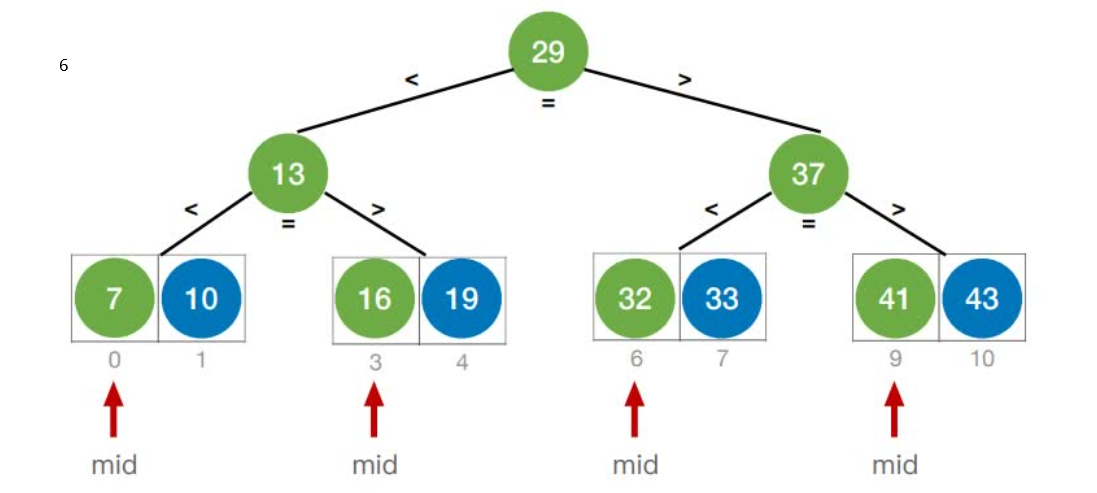
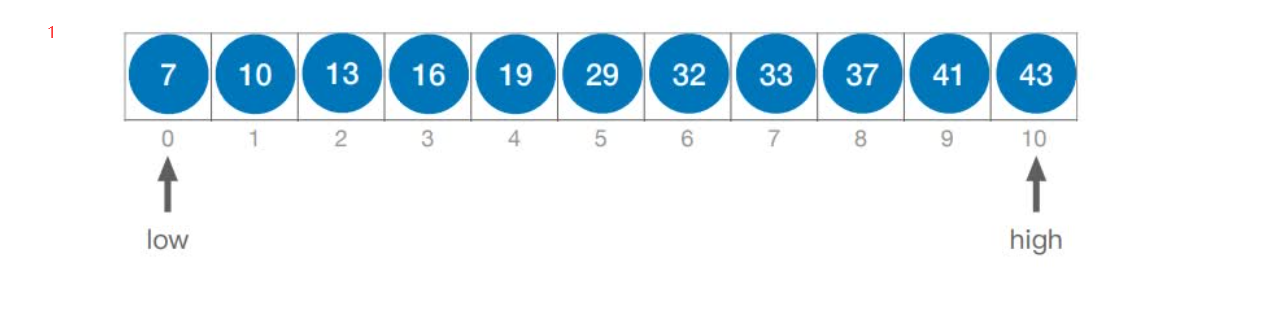
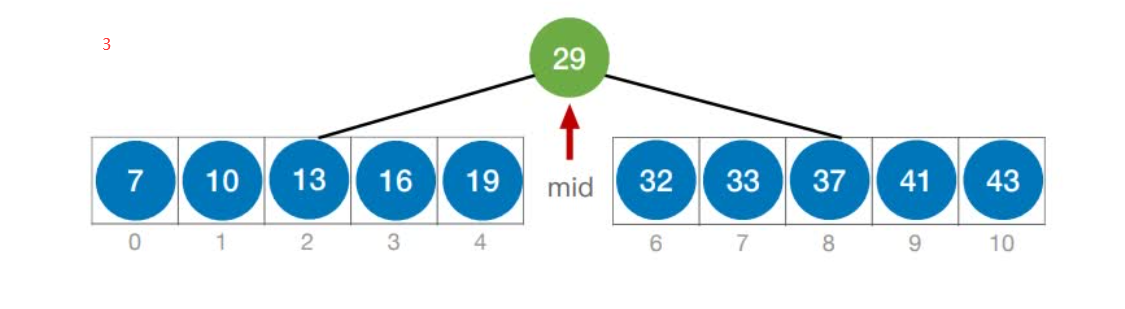
首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

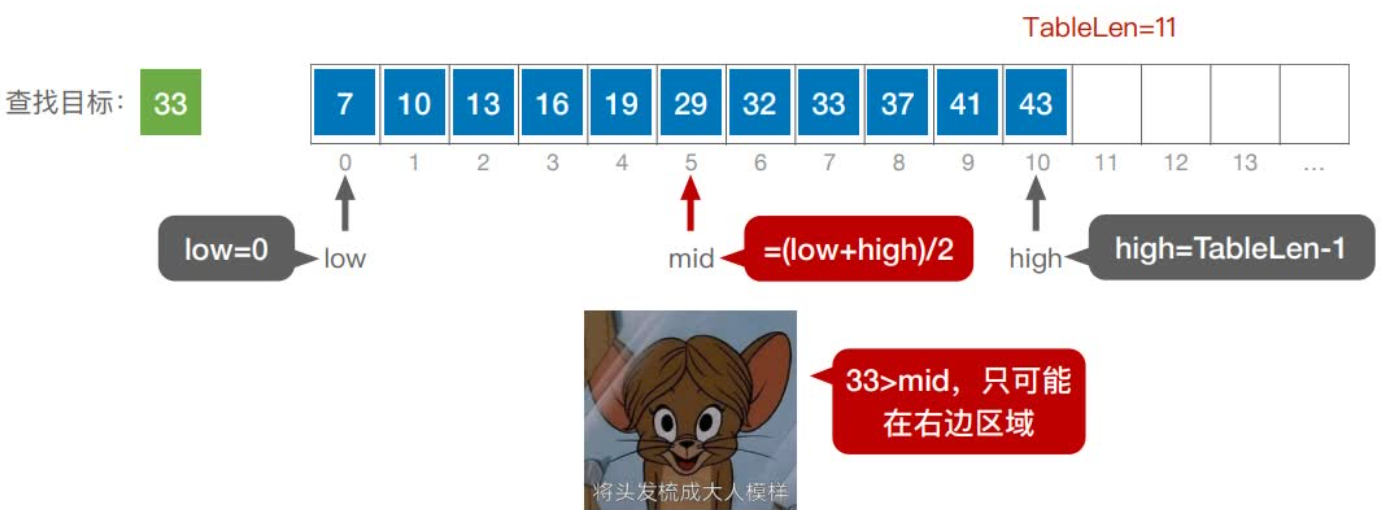
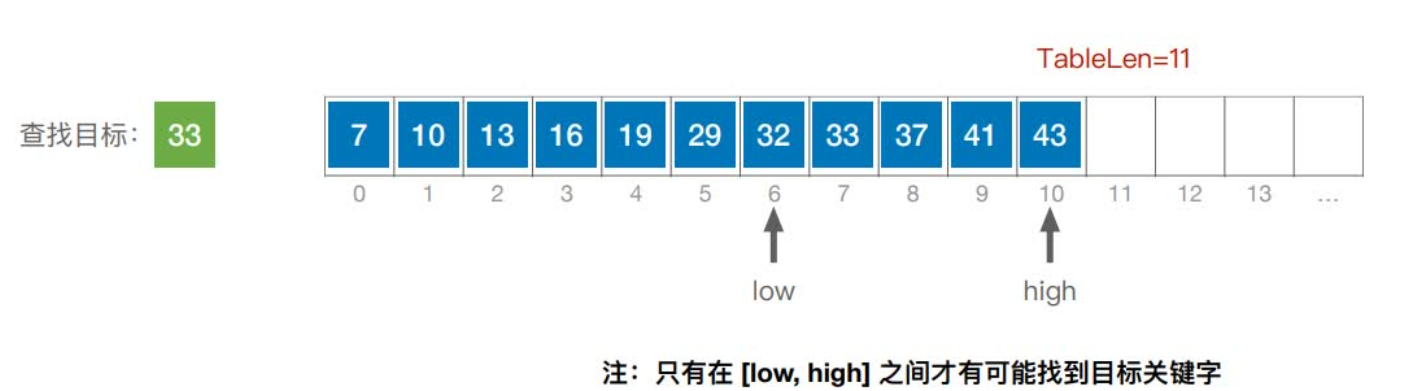
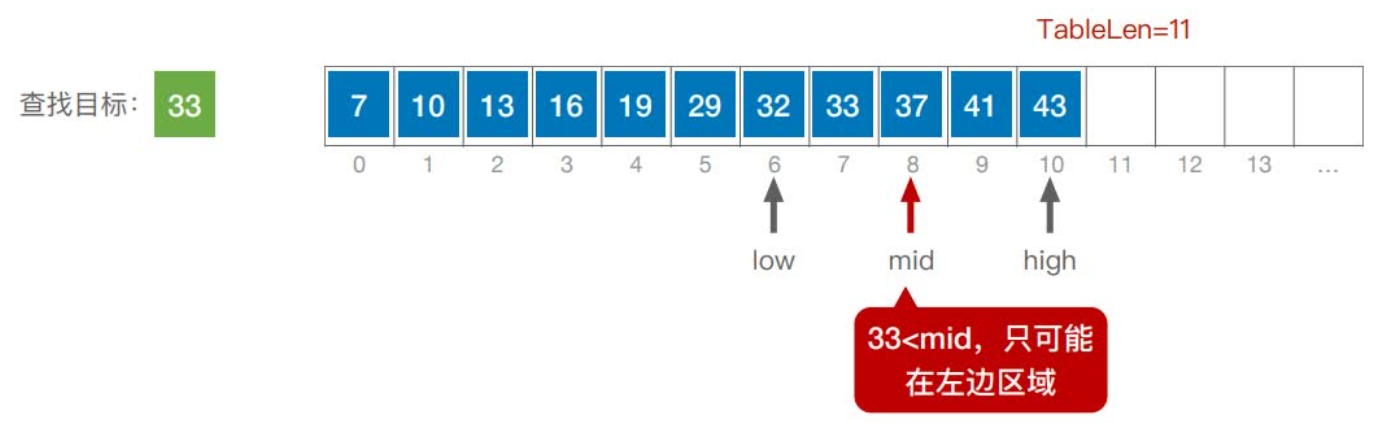
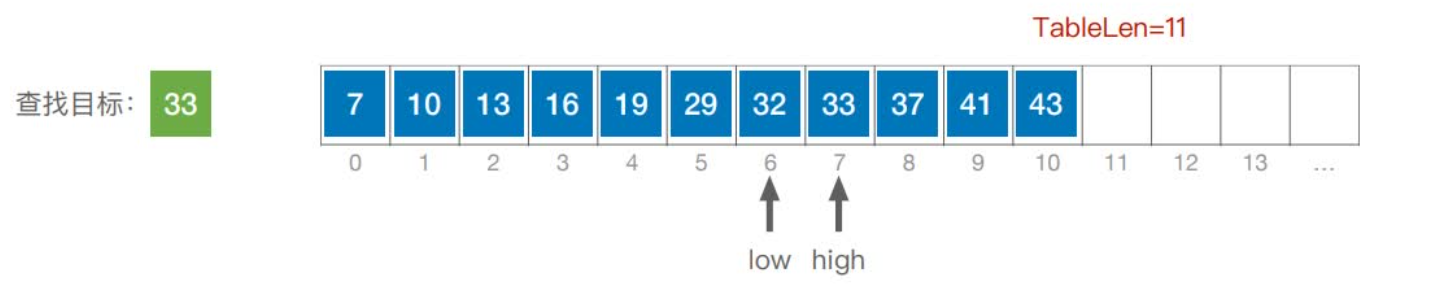
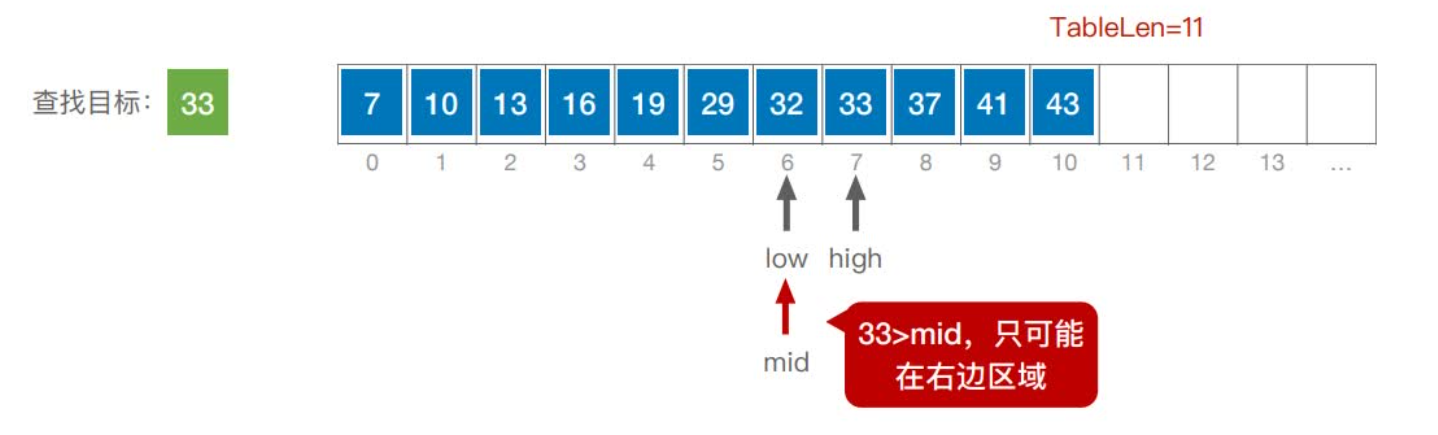
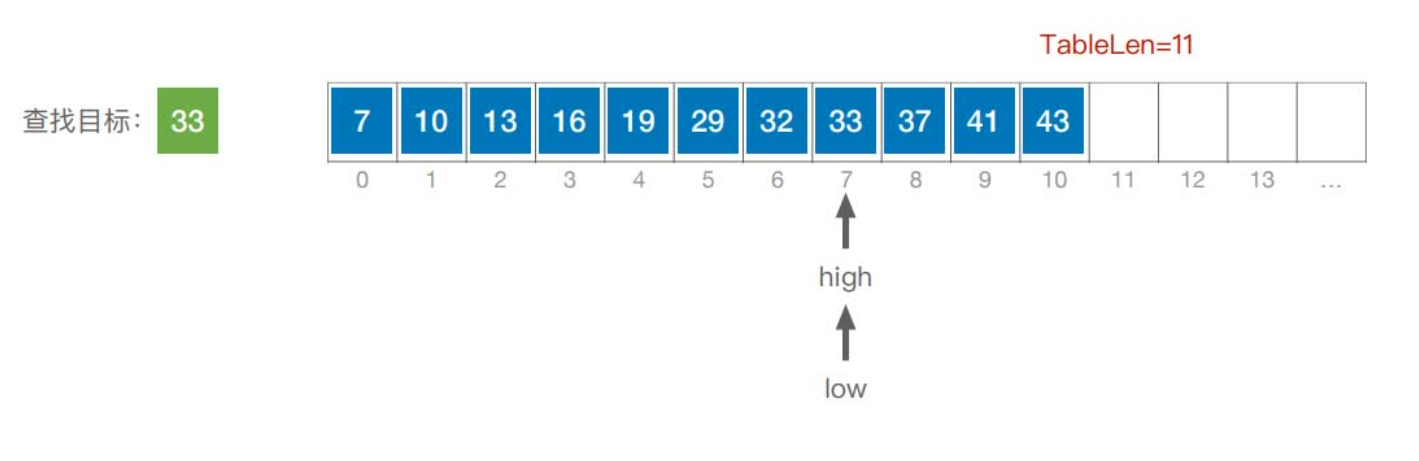
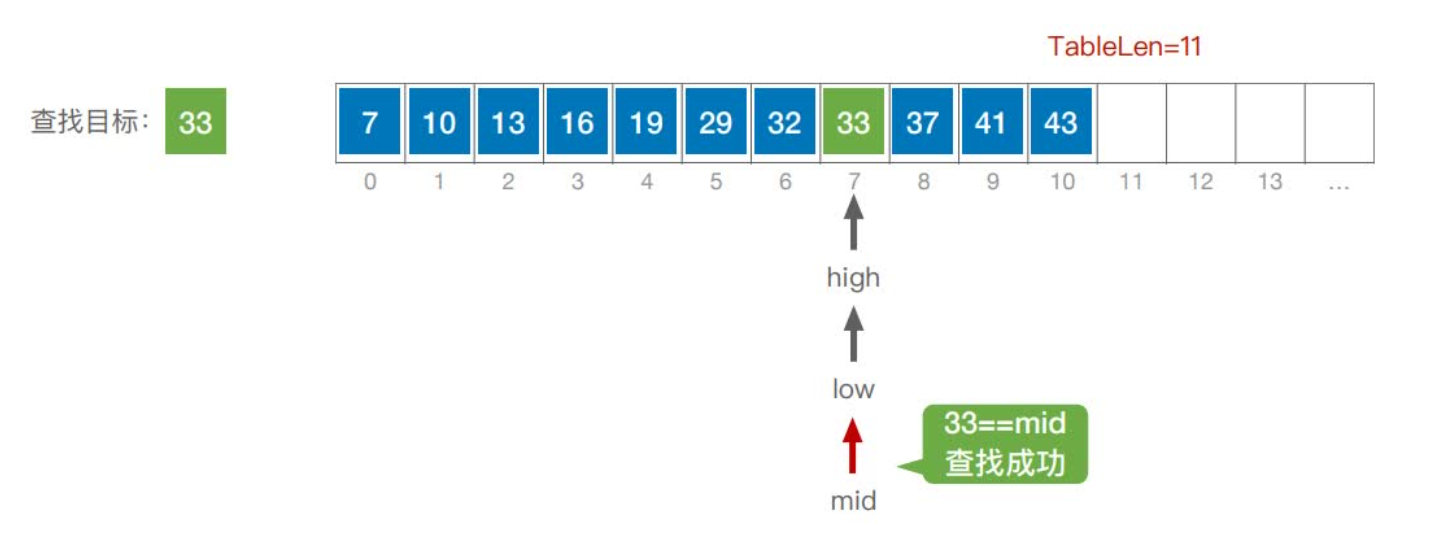
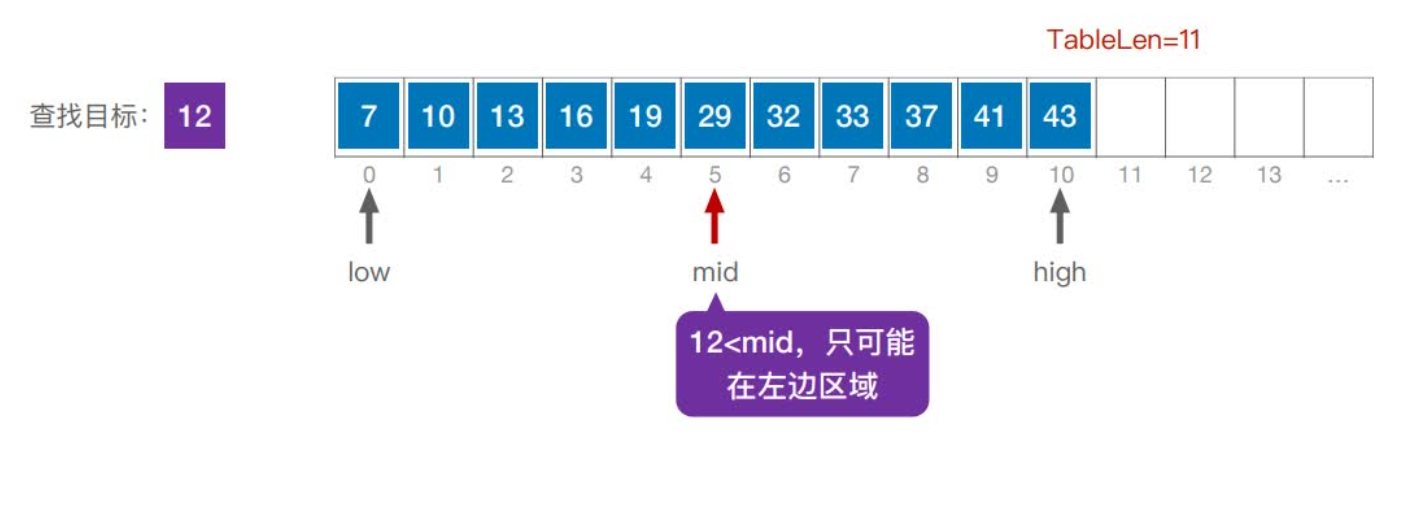
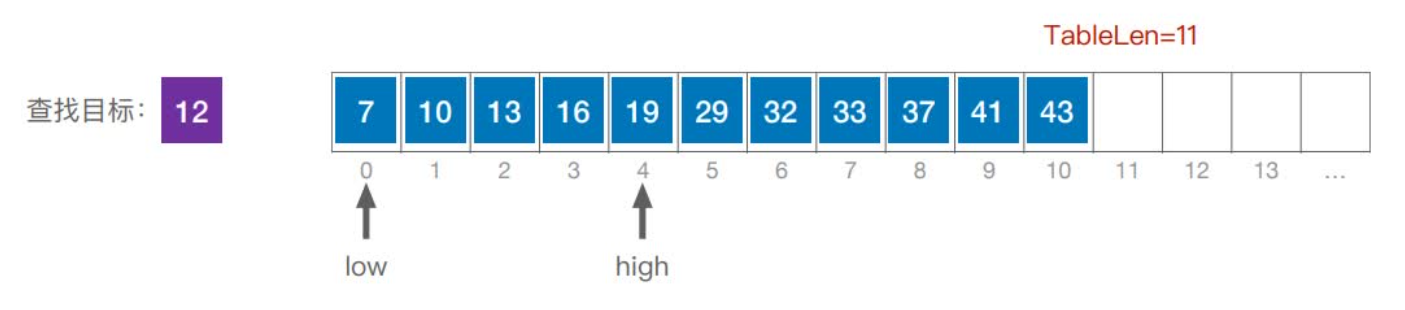
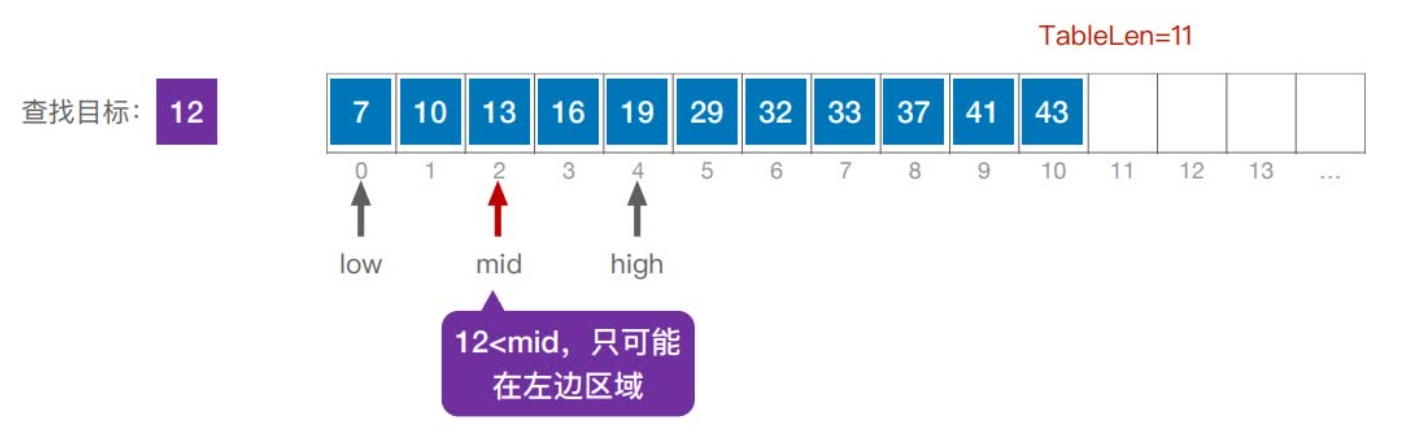
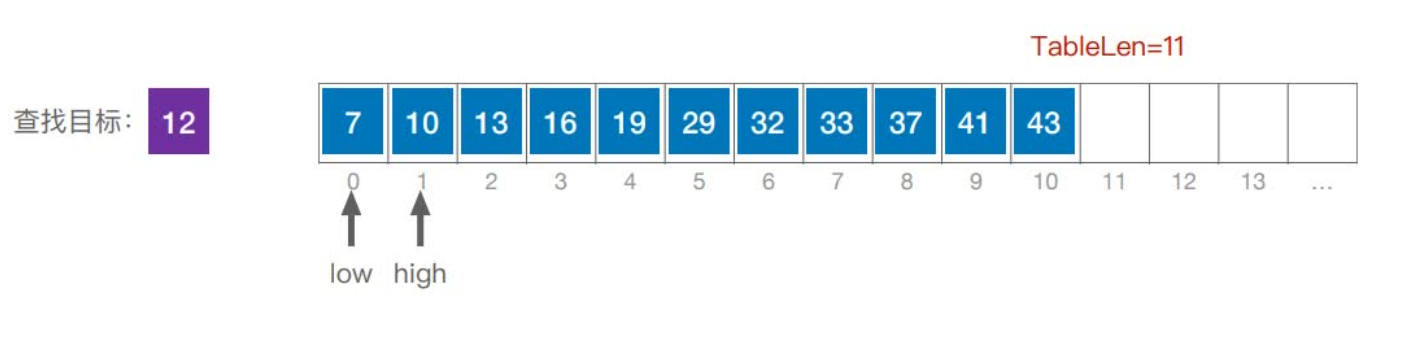
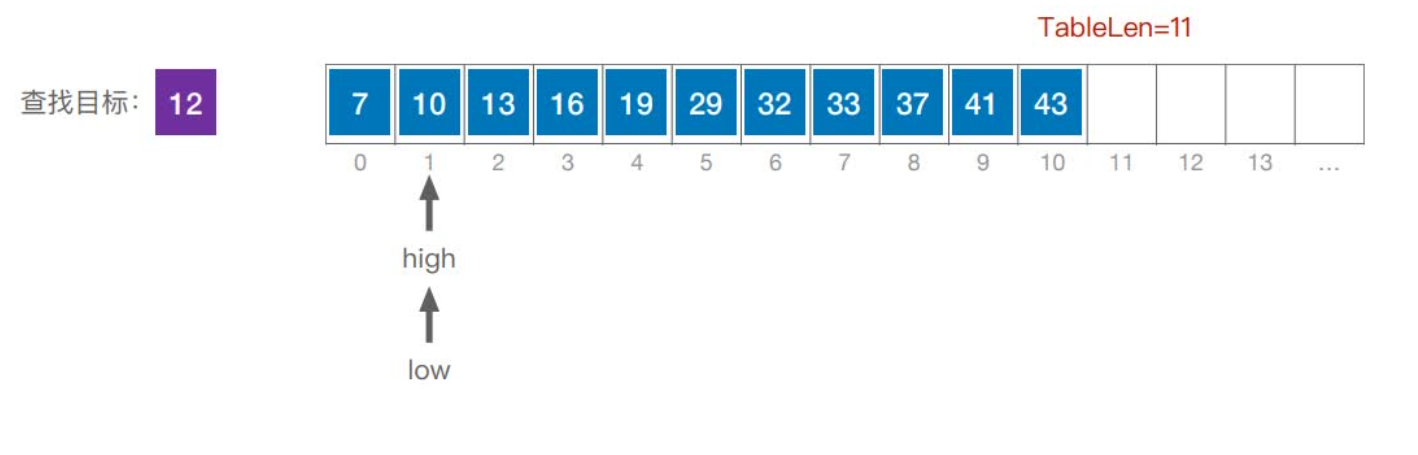
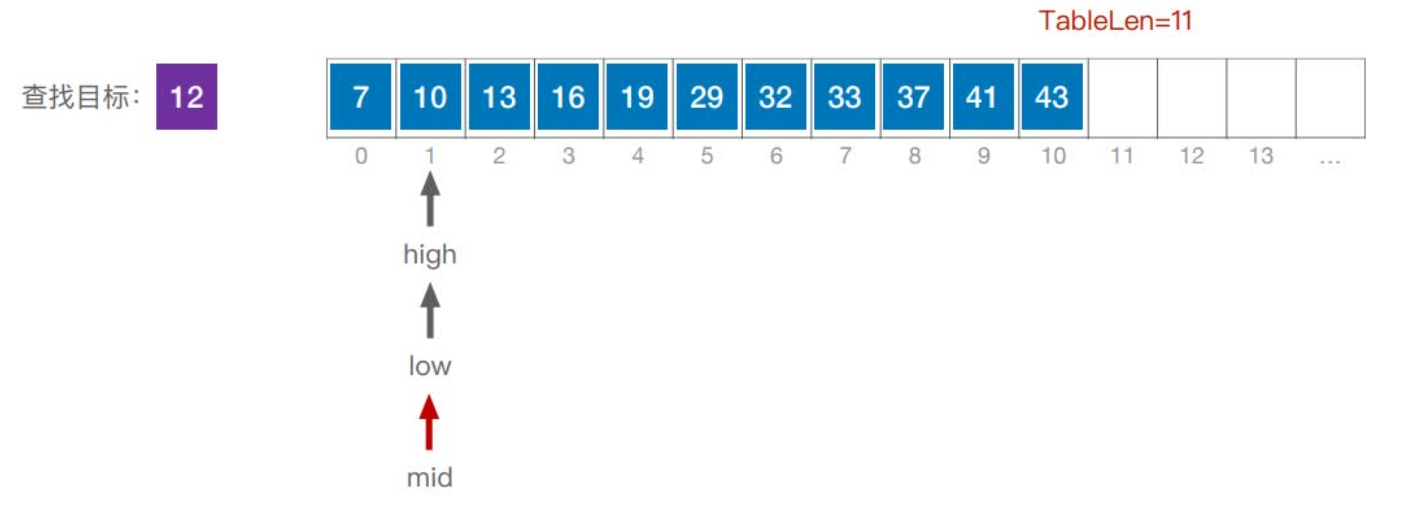
实现

查找效率分析

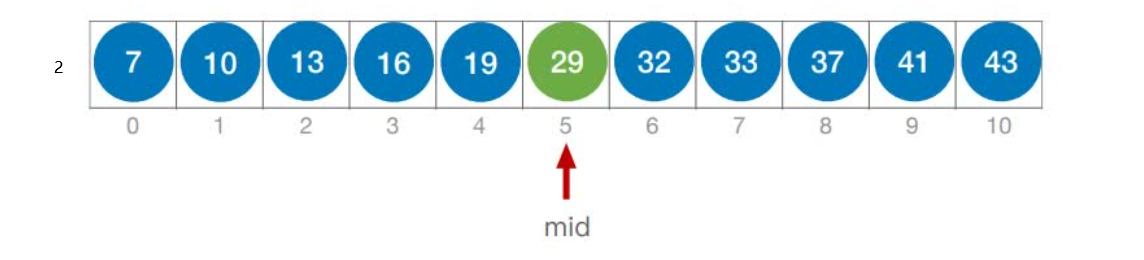
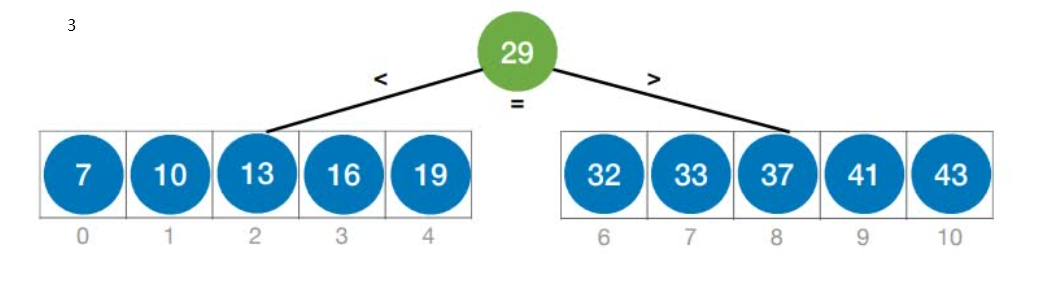
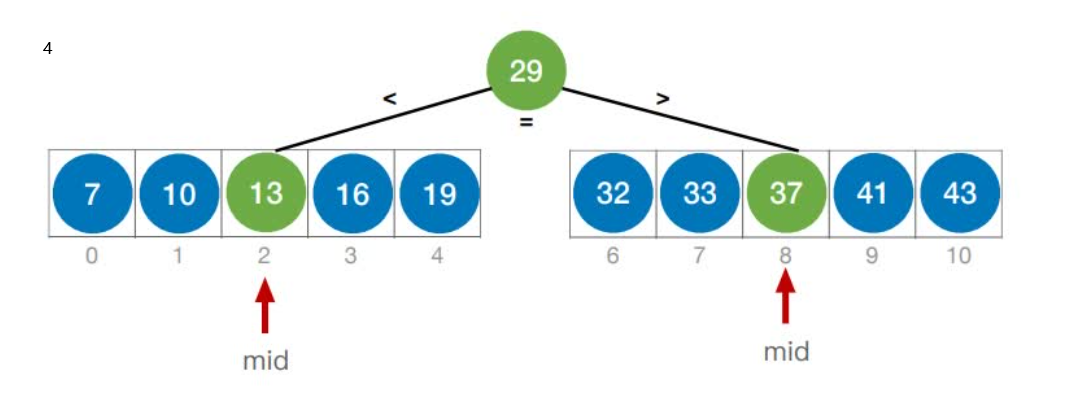
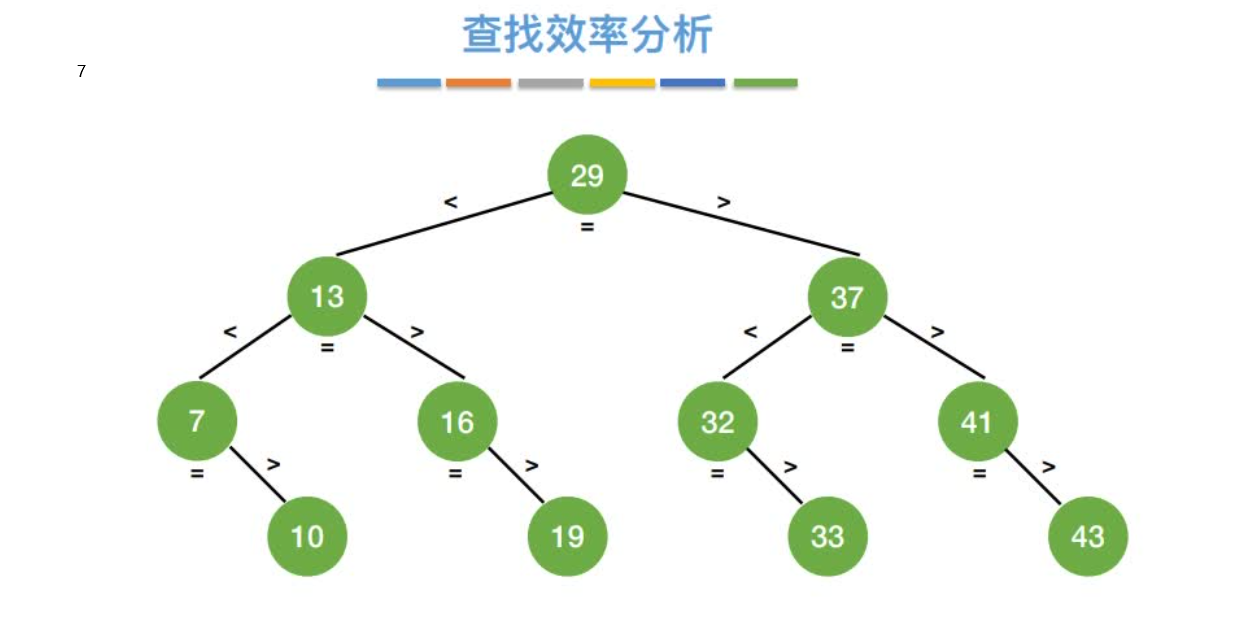
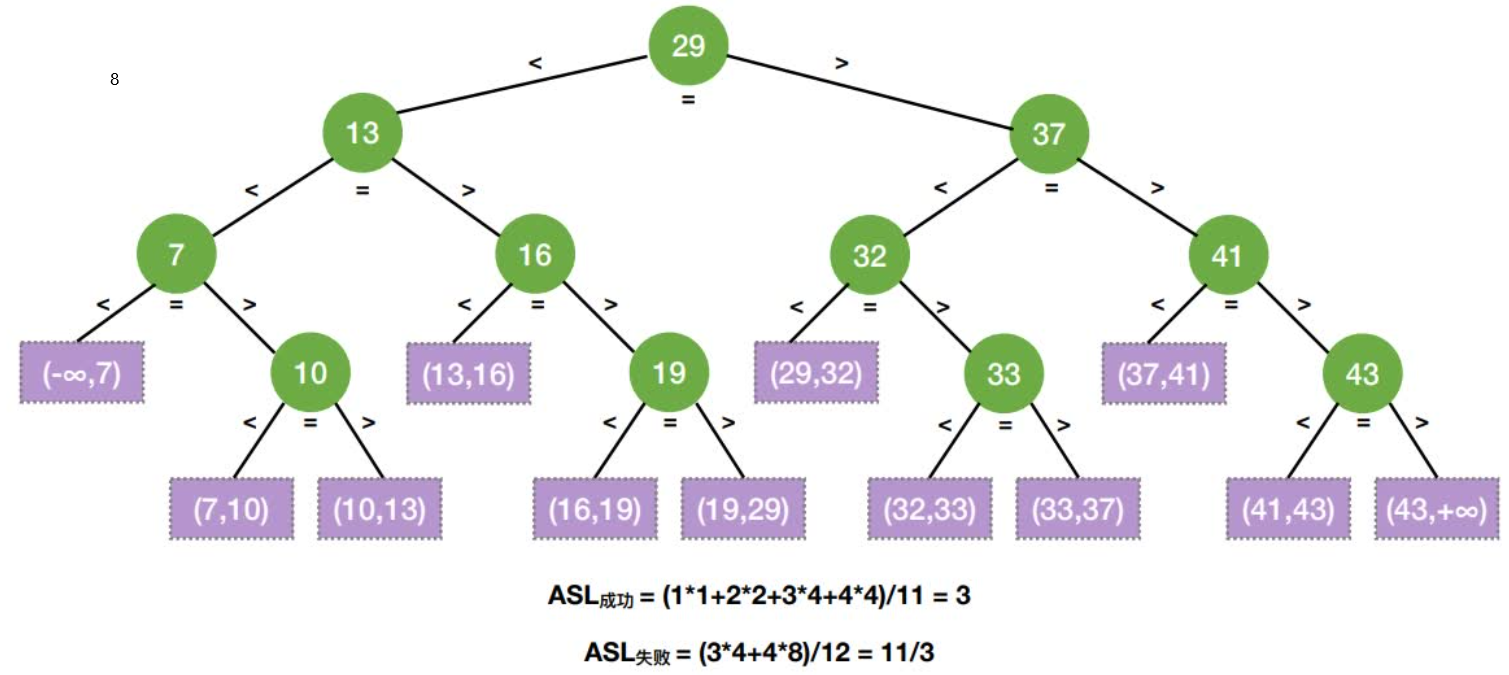
折半查找判定树的构造











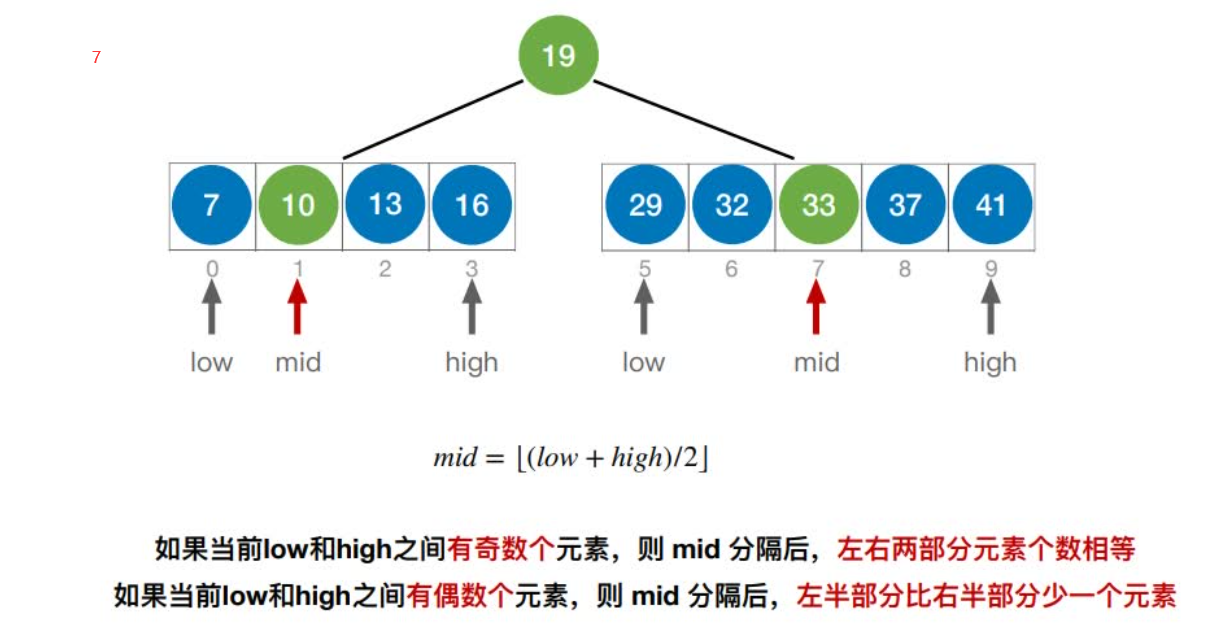
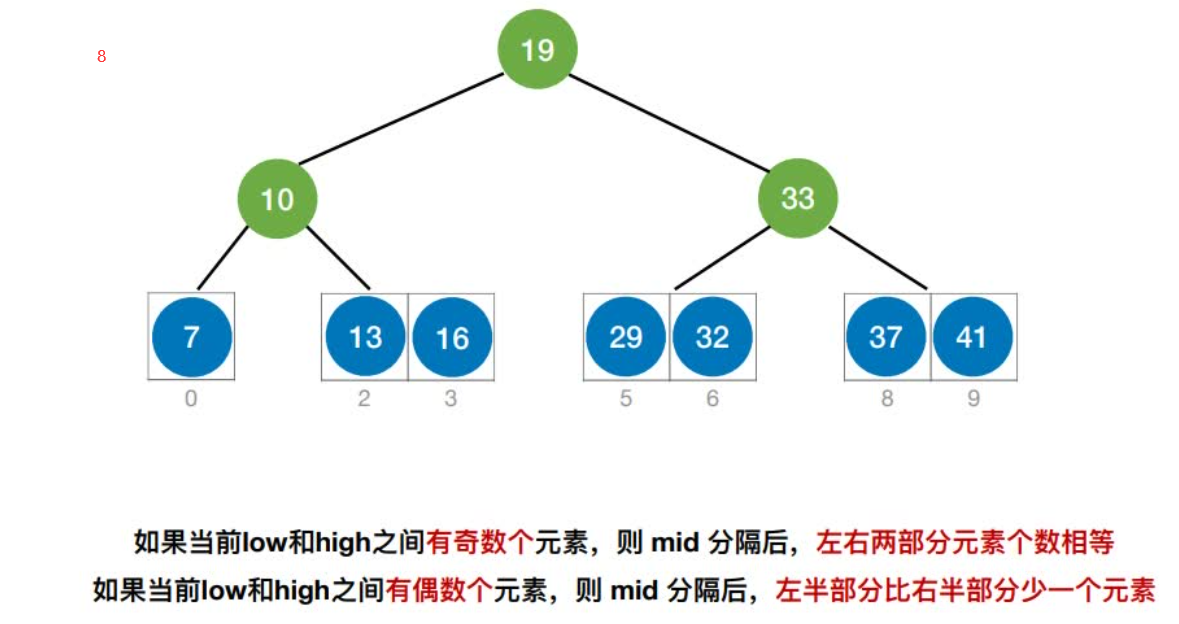
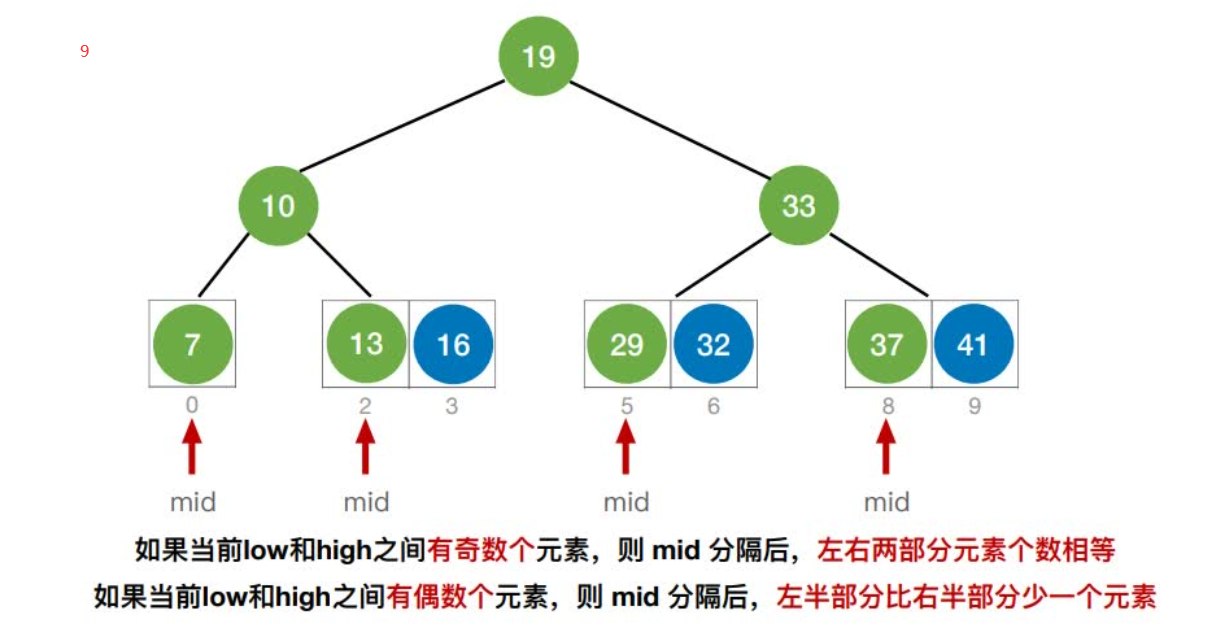
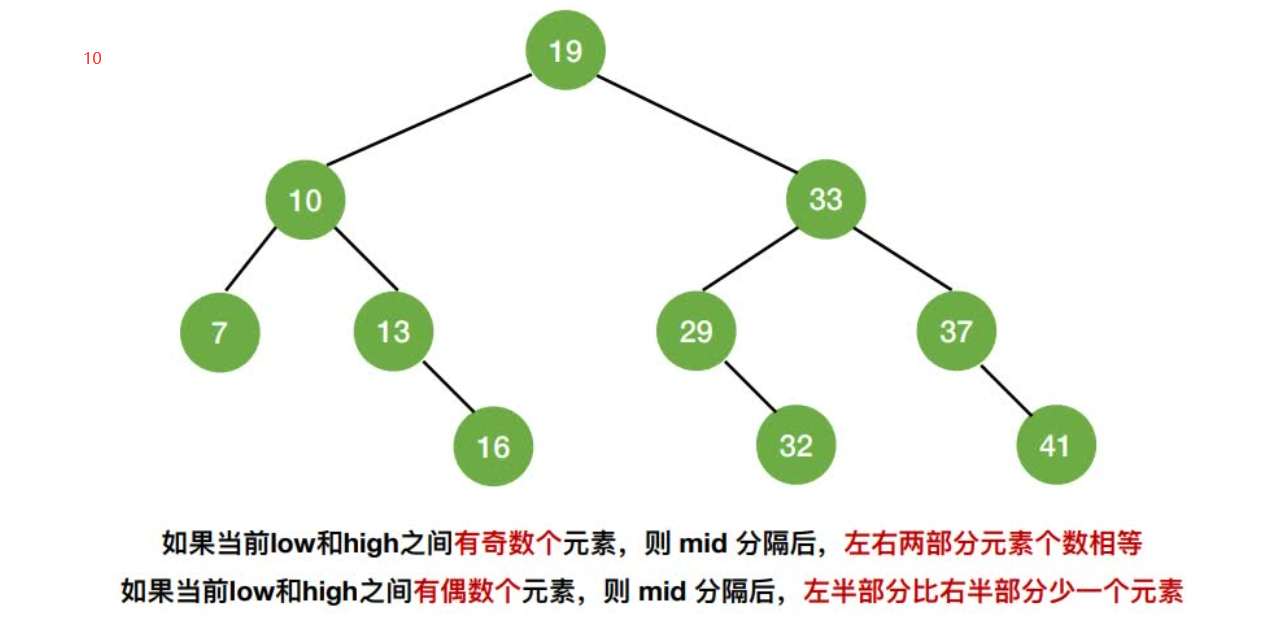
折半查找的判定树⼀定是平衡⼆叉树
折半查找的判定树中，只有最下⾯⼀层是不满的因此，元素个数为n时树⾼h=⌈log2(n+1)⌉
判定树结点关键字：左<中<右，满⾜⼆叉排序树的定义失败结点：n+1个（等于成功结点的空链域数量）
树⾼h=⌈log2(n+1)⌉（注：该树⾼不包含失败结点）
查找失败的ASL≤h
查找成功的ASL≤h
折半查找的时间复杂度=O(log2n)

总结

折半查找时间复杂度=O(log2n)
顺序查找的时间复杂度=O(n)
但折半查找的速度不⼀定⽐顺序查找更快
如果当前low和high之间有奇数个元素，则mid分隔后，左右两部分元素个数相等
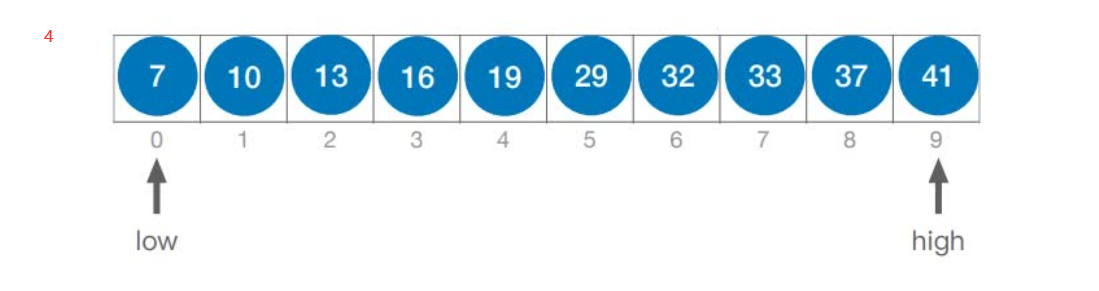
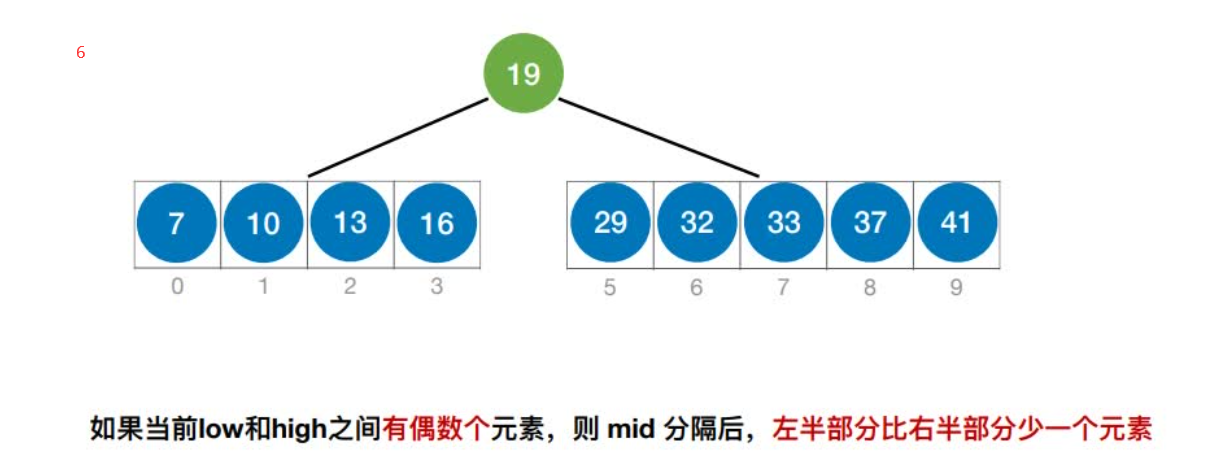
如果当前low和high之间有偶数个元素，则mid分隔后，左半部分⽐右半部分多⼀个元素
折半查找的判定树中，若mid=⌈(low+high)/2⌉，则对于任何⼀个结点，必有：左⼦树结点数-右⼦树结点数=0或1