归并排序详解

一、应用场景

给定一个由 n 个整数组成的数组，用归并排序算法将其从小到大排序。
题源 ： 787. 归并排序 - AcWing题库

二、核心思路

归并排序使用 分治 的算法思想

将原数组分为 两个数组，每个数组中的元素 从小到大 排序。
从前到后同时遍历两个数组，将较小的数组元素放入结果数组中，实现排序

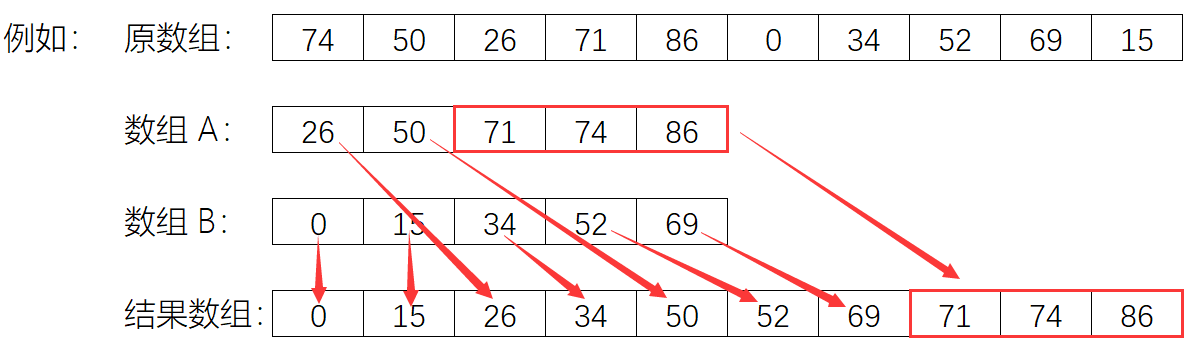{:height=”80%” width=”80%”}

若其中一个数组中元素已经遍历结束，
剩下的元素由于已经有序，只要全部插入到结果末尾，排序完成。

需要解决的问题：

如何将原数组转换为两个排好序的数组 —— 递归思想。

1. 递归具体实现过程的通俗理解（理解的话就跳过这块吧hh）

大白话讲解算法执行过程，理解者请略过。

规定从中间位置（ 下标为 mid 处 ）将数组分为两部分。

​ 要想归并排序 n 个元素的数组，要排好前 n/2 个元素和后 n/2 个元素；
​ 要想归并排序 n/2 个元素的数组，要排前 n/4 个元素和后 n/4 个元素；
​ ······
​ 要想归并排序 5 个元素的数组，要排前 2 个元素和后 3 个元素；
​ 要想归并排序 3 个元素的数组，要排前 1 个元素和后 2 个元素；
​ 要想归并排序 2 个元素的数组，要排前 1 个元素和后 1 个元素。

至此，当数组中的元素只剩下一个，排序完成，向上回溯：

​ 两个 1 元素的数组（天然有序），能形成 2 元素的有序数组，
​ 一个 1 元素数组和一个 2 元素数组，能形成 3 元素的有序数组；
​ 用有序的 2 元素数组和 3 元素数组，能形成有序的 5 元素数组；
​ ······
​ 两个有序的 n/4 元素数组，能形成有序的 n/2 元素数组；
​ 两个有序的 n/2 元素数组，能形成有序的 n 元素数组。

n 个元素有序，排序完成。

三、算法具体实现方法

1. 确定分界点：以数组中间的点为分界，mid = ( l + r ) / 2，mid 为中间数值的 下标 ；

2. 递归排序左段 ( left ) 和右段 ( right )；

3. 归并，将两个有序的数组合并成一个有序的数组，合二为一。

四、函数模板

#include<iostream>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N]; // 存储输入的数据
int tmp[N]; // tmp 数组用于 临时 存放归并的结果 

void merge_sort( int q[], int l, int r ) // l r 是数组元素的真实下标
// 例如：数组中有 10 个元素，下标区间为 [0,9]，所以 l = 0, r = 9，merge_sotr( q, 0, 9 ); 
{
    if( l >= r )    return ; 
    // 如果区间中没有元素，或只有一个元素，就不用再排序了，直接返回 

    int mid = l + r >> 1; // 计算中间元素的 下标
    // 即 mid = ( l + r ) / 2; 

    merge_sort( q, l, mid ), merge_sort( q, mid + 1, r ); 
    // 以中间元素为分界，递归排序前后两个数组 

    int k = 0; // k 表示已经合并了几个数了
    int i = l, j = mid + 1; // i j 为两个指针，初值指向数组的两段的起始元素

    while( i <= mid && j <= r ) // 当两个数组均未遍历完，将较小的值存入 tmp 数组 
        if( q[i] <= q[j] )  tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    // 由于 i j 在每次赋值后会自增，到最后会超过各自数值段的边界
    // 即 最终 i == mid + 1，或 j == r + 1，使得上面循环结束 

    while( i <= mid ) tmp[k++] = q[i++];
    while( j <= r ) tmp[k++] = q[j++]; 
    // 其中一个数组遍历完了，剩下的元素插入 tmp 数组的末尾 

    for( i = l, j = 0; i <=r; i++, j++ )    q[i] = tmp[j];
    // 将 tmp 数组中的元素存入 原数组 中 
}   
int main()
{
    printf("\n 请输入要排序的数组元素的个数："); 
    scanf( "%d", &n ); 
    printf("\n 请输入 %d 个整数：", n);

    for( int i = 0; i < n; i++ )    scanf( "%d", &q[i] );

    merge_sort( q, 0, n - 1 );
    printf("\n 排序后的数列为：", n);
    for( int i = 0; i < n; i++ )    printf( "%d ", q[i] );
    return 0;
}

五、易错点及原因分析

① 递归结束条件遗漏

​ 函数最开始的判断是递归结束的条件，若遗漏会导致死循环。

if( l >= r ) return ; 

② 归并前指针初始值设置错误

​ 指针 i 的初始值为数组的起始元素 l ( 左指针 L )
​ 指针 j 的初始值为第二段数组的起始元素 mid + 1

③ 函数的调用

​ 调用函数时，传入的区间参数 l / r 是数组元素的 真实下标，
​ 例如：数组 q 中有 10 个元素，下标区间为 [ 0 , 9 ] ，
​ 所以 l = 0, r = 9，merge_sort( q, 0, 9 );

④ 最后需要将 tmp 数组中的元素存入 原数组 中

​ 由于每次调用函数时，给出的区间为数组元素的真实的下标 l 和 r，
​ 所以数组元素的个数为 ( r - l + 1 )，
​ 所以 for 循环从 i == l 到 i == r 。

​ 而 tmp 数组每次更新，下标均从 0 开始，
​ 所以 tmp 数组的下标 j 要从 0 开始。

⑤ mid 的取值不能为 ( l + r ) / 2 + 1

​ mid 作为一个下标，作用是将原数组分为前后两段，
​ 前后两段的区间为：[ l , mid ] 和 [ mid + 1 , r ]

​ 若 mid 取 ( l + r ) / 2 + 1，在递归的过程中，
​ 当数据段中只有两个元素，假设该段的区间为 [ 0 , 1 ]
​ 则下次递归时的区间为：[ 0 , 1 ] 和 [ 2 , 1 ] ，会陷入死循环。
​ ( 从 [ 0 , 1 ] 递归到 [ 0 , 1 ] )

六、函数时间复杂度分析

双路归并，合二为一。
归并这个步骤，每个元素只会被比较一次，时间复杂度为 $O(\,n\,)$
又有 ${\log _2}n$ 层的归并。

所以时间复杂度为：$O(\,n{\log _2}n\,)$

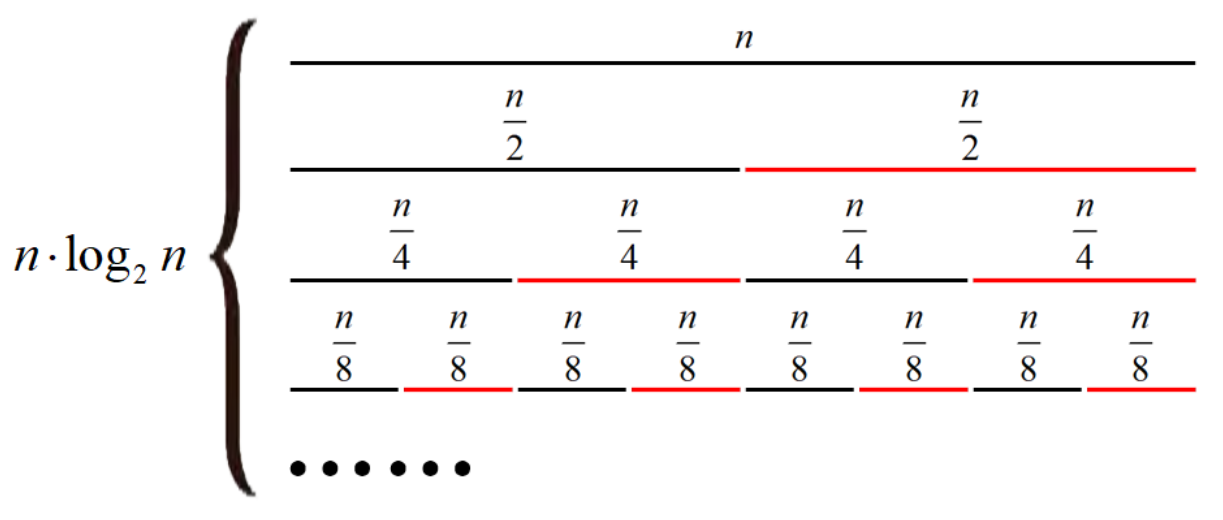{:height=”70%” width=”70%”}

七、补充：排序方法是稳定的

“ 稳定 ” 是指原序列中两个 相同的数值，在排序完成后，其 先后位置没有发生变化。
如果两个相同的数值的位置可能发生变化，则说明这种排序方法是不稳定的。

本模板 中的归并排序算法，由于归并时的判断，
使得若遇到相同元素，则按原来的顺序排列，排序方法稳定。

if( q[i] <= q[j] )  tmp[k++] = q[i++];
else tmp[k++] = q[j++];

八、( 无注释版 ) 函数模板

#include<iostream>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N], tmp[N];

void merge_sort( int q[], int l, int r )
{
    if( l >= r )    return ;
    int mid = l + r >> 1;

    merge_sort( q, l, mid), merge_sort( q, mid + 1, r );

    int k = 0, i = l, j = mid + 1;
    while( i <= mid && j <= r)
        if( q[i] <= q[j] )  tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while( i <= mid) tmp[k++] = q[i++];
    while( j <= r ) tmp[k++] = q[j++];

    for(  i = l, j = 0; i <= r; i++, j++ )  q[i] = tmp[j];
}

int main()
{
    printf("\n 请输入要排序的数组元素的个数："); 
    scanf( "%d", &n ); 
    printf("\n 请输入 %d 个整数：", n);

    for( int i = 0; i < n; i++ )    scanf( "%d", &q[i] );

    merge_sort( q, 0, n - 1 );
    printf("\n 排序后的数列为：", n);
    for( int i = 0; i < n; i++ )    printf( "%d ", q[i] );
    return 0;
}

九、参考资料

y 总的课~~

（接受批评指正，欢迎交流补充~~ XD）