题目背景

裴蜀定理：
裴蜀定理（或贝祖定理）得名于法国数学家艾蒂安·裴蜀，说明了对任何整数$a$、$b$和它们的最大公约数$d$，关于未知数$x$和$y$的线性不定方程（称为裴蜀等式）：若$a$,$b$是整数,且$gcd(a,b)=d$，那么对于任意的整数$x$,$y$,$ax+by$都一定是$d$的倍数，特别地，一定存在整数$x$,$y$，使$ax+by=d$成立。

裴蜀定理证明：

现要求用扩展欧几里得方法，对每两个正整数a，b

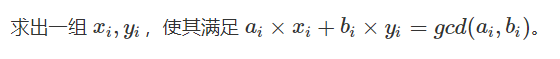
思路

模板代码

//题目背景：AcWing 877
#include<iostream>
using namespace std;
void exgcd(int a,int b,int &x,int &y)  //扩展欧几里得算法
{
    if(!b)  //递归边界，b为0了
    {
        x=1,y=0;  //这个时候最大公约数是a，很容易想到x=1，y=0这个组合
        return;   //一定要记得return掉，这时候递归终结了
    }
    exgcd(b,a%b,x,y); //没到边界，继续往下递归
    int t=x;     //接用下层递归的结果，根据上面的推导，更新下当前层的最新x，y值
    x=y;
    y=t-a/b*y;
}
int main()
{
    int n,a,b,x,y;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
    return 0;
}
}

应用：求解线性同余方程

为什么最后的结果要$\%m$?
题目中要求“输出答案必须在int范围之内”，而算到的x可能会溢出，根据$(a\times x) \% m = (a \times (x \% m)) \% m$，所以保险起见输出为$x \% m$

#include<iostream>
using namespace std;
typedef long long LL;
int exgcd(int a,int b,int &x,int &y)  //扩展欧几里得算法
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    int ans=exgcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return ans;
}
int main()
{
    int n,a,b,m,x,y;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d%d",&a,&b,&m);
        int ans=exgcd(a,m,x,y);
        if(b%ans!=0) puts("impossible");   //如果b不能整除a和m的最大公因数，那么不存在
        else printf("%ld\n",(LL)x*b/ans%m);
    }              //这里用（LL）是为了防止x*b的中间结果溢出了
    return 0;      //这里%m是为了使结果留在int范围内，具体原因在上面
}