问题背景

快速求解a^b^ % p的问题
时间复杂度:$O(logb)$
若对于n组数据,那么时间复杂度为$O(n\times logb)$

思路

模板代码

//题目背景：AcWing 875
LL qmi(int a,int b,int p)  //求a的b次方对p取模的值
{
    LL res=1%p;  //res初值为1%p，为什么这么写，见后面注释
    while(b)  //b在循环中不断右移，b不等于0
    {
        if(b&1) res=res*a%p;   //如果b的最后一位为1，就把结果乘上a的当前次方的值
        a=a*(LL)a%p;  //a在循环中不断平方，(LL)这是为了让a的值不溢出
        b=b>>1;   //b右移
    }
    return res;  //返回答案
}

LL res=1%p;

为什么这么写？
因为当b等于0时，后面那个while进不去，这时候如果p等于1，加上%p的话结果res是0，不加上p的结果res是1。
而实际结果也应该是0，所以要加上%p更保险！

应用：快速幂求乘法逆元

乘法逆元定义

若整数 $b$，$m$ 互质，并且对于任意的整数 $a$，如果满足 $b|a$，则存在一个整数 $x$，使得 $a/b≡a×x(mod\quad m)$，则称 $x$ 为 $b$ 的模 $m$ 乘法逆元，记为 $b^{−1}(mod\quad m)$。
$b$ 存在乘法逆元的充要条件是 $b$ 与模数 $m$ 互质。当模数 $m$ 为质数时，$b^{m−2}$ 即为 $b$ 的乘法逆元。

公式推导

因为$a/b≡a×b^{−1}(mod\quad m)$
所以$b\times a/b≡b\times a×b^{−1}(mod\quad m)$
即$a≡b\times a×b^{−1}(mod\quad m)$
即$1≡b\times b^{−1}(mod\quad m)$
由费马小定理：（p为质数）

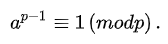
得：

$b^{−1}=b^{m-2}$
$b$ 存在乘法逆元的充要条件是 $b$ 与模数 $m$ 互质
由上述推导，即将求乘法逆元得过程，转化为求快速幂的过程。

参考代码

//题目背景：AcWing 876
#include<iostream>
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p)  //求快速幂的模板
{
    LL res=1%p;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*(LL)a%p;
        b=b>>1;
    }
    return res;
}
int main()
{
    int n,a,p;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d",&a,&p);
        if(a%p==0) puts("impossible");  //题目中限定了p是质数，a和p有公因数，那说明a一定比p大，所以这里判断a和p是否互质，直接看a是不是p的倍数
        else printf("%d\n",qmi(a,p-2,p));
    }
    return 0;
}