下面的两个模板代码以 Acwing 1171.距离 为背景

树上倍增法：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N = 50010;

int f[N][20],d[N],dist[N];//d[i]表示表示点i的深度，f[x][k]表示点x向上走2^k步所到达的点(x的2^k级祖先)
//dist[i]表示节点i到根节点的距离
int e[2*N], ne[2*N], w[2*N], h[N], idx;
int n, m, dep;//dep表示树的深度
queue<int> q;

void add(int a, int b, int c){
    e[idx]=b, w[idx]=c, ne[idx]=h[a], h[a]=idx++;
}
void bfs(){//预处理，宽搜不容易因为递归层数过多爆栈
//记录各个点的深度和他们2^i级的的祖先，用数组d[]表示每个节点的深度，f[i][j]表示节点i的2^j 级祖先
    q.push(1);

    memset(d,0x3f,sizeof d);
    d[0] = 0;//d[0]=0是哨兵
    d[1]=1;
    while(q.size()){
        int t=q.front();
        q.pop();

        for(int i=h[t]; ~i; i=ne[i]){
            int j=e[i];
            if(d[j]>d[t]+1){//说明j还没被搜索过
                d[j]=d[t]+1;
                f[j][0]=t;
                q.push(j);//把第depth[j]层的j加进队列

                dist[j]=dist[t]+w[i];

                for(int k=1; k<=dep; k++)
                   f[j][k]=f[f[j][k-1]][k-1];
            }

        }
    }
}
int lca(int x,int y){
    if(d[x] < d[y])  swap(x,y);//不妨设x的深度 >= y的深度

    for(int i = dep; i >= 0; i--)
        if(d[f[x][i]] >= d[y]) x = f[x][i];//先跳到同一深度

    if(x==y) return x;//如果x是y的祖先，那他们的LCA肯定就是x了

    for(int i = dep; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
        //因为我们要跳到它们LCA的下面一层，所以它们肯定不相等，如果不相等就跳过去。

    return f[x][0];//返回父节点，即LCA
}
int main(){
    memset(h,-1,sizeof h);
    ios::sync_with_stdio(0);
    cin>>n>>m;
    dep=(int)(log(n)/log(2))+1;

    for(int i=0;i<n-1;i++){
        int a, b, c;
        cin>>a>>b>>c;
        add(a,b,c), add(b,a,c);
    }

    bfs();

    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        int t = lca(a,b);
        int ans = dist[a] + dist[b] - dist[t] * 2;
        //树上两个点a，b之间的距离等于a到根节点+b到根节点的距离-LCA(a,b)到根节点的距离
        cout<<ans<<endl;
    }

    return 0;
}

Tarjan算法

个人感觉这样还是有很多人不太理解，所以我打算模拟一遍给大家看
假设我们有一组数据 9个节点 8条边 联通情况如下：

1–2，1–3，2–4，2–5，3–6，5–7，5–8，7–9 即下图所示的树

设我们要查找最近公共祖先的点为9–8，4–6，7–5，5–3；

设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;　


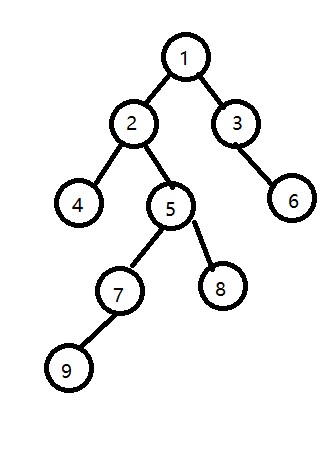
　　　　下面开始模拟过程：

取1为根节点，往下搜索发现有两个儿子2和3；

先搜2，发现2有两个儿子4和5，先搜索4，发现4没有子节点，则寻找与其有关系的点；

发现6与4有关系，但是vis[6]=0，即6还没被搜过，所以不操作；

发现没有和4有询问关系的点了，返回此前一次搜索，更新vis[4]=1；

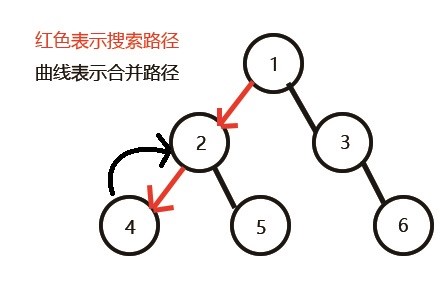
表示4已经被搜完，更新f[4]=2，继续搜5，发现5有两个儿子7和8;

先搜7，发现7有一个子节点9，搜索9，发现没有子节点，寻找与其有关系的点；

发现8和9有关系，但是vis[8]=0,即8没被搜到过，所以不操作；

发现没有和9有询问关系的点了，返回此前一次搜索，更新vis[9]=1；

表示9已经被搜完，更新f[9]=7，发现7没有没被搜过的子节点了，寻找与其有关系的点；

发现5和7有关系，但是vis[5]=0，所以不操作；

发现没有和7有关系的点了，返回此前一次搜索，更新vis[7]=1；

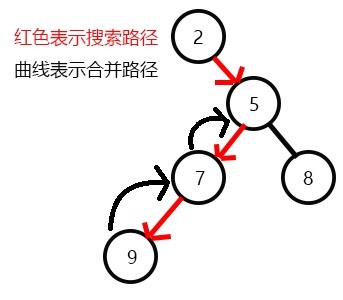
表示7已经被搜完，更新f[7]=5，继续搜8，发现8没有子节点，则寻找与其有关系的点；

发现9与8有关系，此时vis[9]=1，则他们的最近公共祖先为find(9)=5；

(find(9)的顺序为f[9]=7–>f[7]=5–>f[5]=5 return 5;)

发现没有与8有关系的点了，返回此前一次搜索，更新vis[8]=1；

表示8已经被搜完，更新f[8]=5，发现5没有没搜过的子节点了，寻找与其有关系的点；

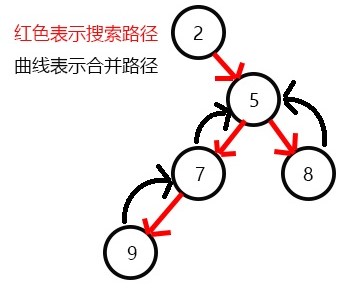
　　　　发现7和5有关系，此时vis[7]=1，所以他们的最近公共祖先为find(7)=5；

(find(7)的顺序为f[7]=5–>f[5]=5 return 5;)

又发现5和3有关系，但是vis[3]=0，所以不操作，此时5的子节点全部搜完了；

返回此前一次搜索，更新vis[5]=1，表示5已经被搜完，更新f[5]=2；

发现2没有未被搜完的子节点，寻找与其有关系的点；

又发现没有和2有关系的点，则此前一次搜索，更新vis[2]=1；

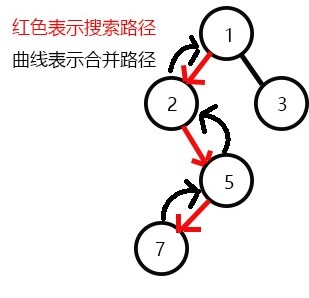
　　　　表示2已经被搜完，更新f[2]=1，继续搜3，发现3有一个子节点6；

搜索6，发现6没有子节点，则寻找与6有关系的点，发现4和6有关系；

此时vis[4]=1，所以它们的最近公共祖先为find(4)=1;

(find(4)的顺序为f[4]=2–>f[2]=2–>f[1]=1 return 1;)

发现没有与6有关系的点了，返回此前一次搜索，更新vis[6]=1，表示6已经被搜完了；

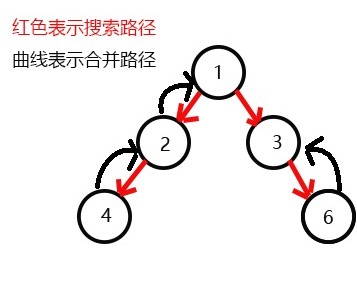
　　　　更新f[6]=3，发现3没有没被搜过的子节点了，则寻找与3有关系的点；

发现5和3有关系，此时vis[5]=1，则它们的最近公共祖先为find(5)=1；

(find(5)的顺序为f[5]=2–>f[2]=1–>f[1]=1 return 1;)

发现没有和3有关系的点了，返回此前一次搜索，更新vis[3]=1；

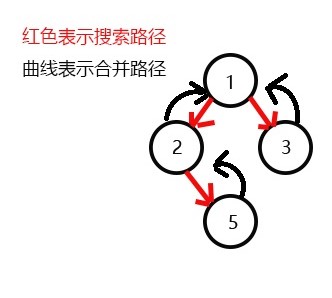
　　　　更新f[3]=1，发现1没有被搜过的子节点也没有有关系的点，此时可以退出整个dfs了。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

typedef pair<int, int> PII;

const int N = 10010, M = N * 2;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];//每个点和1号点的距离
int p[N];
int res[M];
int st[N];
vector<PII> query[N];//把询问存下来   
// query[i][first][second] first存查询距离i的另外一个点j，second存查询编号idx

void add(int a,int b,int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int find(int x)
{
    if(p[x]!=x)p[x] = find(p[x]);
    return p[x];
}

void dfs(int u,int fa)
{
    for(int i=h[u];~i;i=ne[i])
    {
        int j = e[i];
        if(j==fa) continue;
        dist[j] = dist[u]+w[i];
        dfs(j,u);
    }
}

void tarjan(int u)
{
    st[u]=1;//当前路径点标记为1
    // u这条路上的根节点的左下的点用并查集合并到根节点
    for(int i = h[u]; ~i ;i=ne[i])
    {
        int j = e[i];
        if(!st[j])//先递归，再赋值，因为要使这颗子树都递归过了
        {
            tarjan(j);//往左下搜
            p[j] = u;//从左下回溯后把左下的点合并到根节点
        }
    }
    // 对于当前点u 搜索所有和u
    for(auto item:query[u])
    {
        int y = item.first,id = item.second;
        if(st[y]==2)//如果查询的这个点已经是左下的点(已经搜索过且回溯过,标记为2)
        {
            int anc = find(y);//y的根节点
            // x到y的距离 = d[x]+d[y] - 2*d[lca] 
            res[id] = dist[u]+dist[y] - dist[anc]*2;//第idx次查询的结果 res[idx]
        }
    }
    //点u已经搜索完且要回溯了 就把st[u]标记为2 
    st[u] = 2;
}

int main()
{
    cin >> n >> m;
    // 建图
    memset(h,-1,sizeof h);
    for(int i=0;i<n-1;i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(a,b,c),add(b,a,c);
    }

    // 存下询问
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin >> a >> b;
        if(a!=b)
        {
            query[a].push_back({b,i});
            query[b].push_back({a,i});
        }
    }
    for(int i=1;i<=n;i++)p[i] = i;

    dfs(1,-1);
    tarjan(1);
    for(int i=0;i<m;i++)cout << res[i] << '\n';//把每次询问的答案输出
    return 0;
}