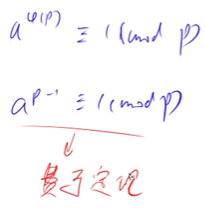欧拉函数定义

欧拉函数证明

1∼N 中与 N 互质的数的个数被称为欧拉函数，求欧拉函数的值，其实就是在计算1∼N 中与 N 互质的数的个数。
首先把N分解质因数，然后再逐步把与N不互质的数去掉，即质因子的倍数，在去的过程中可能出现多去了的情况，这时要补上。

计算欧拉函数代码分析

直接用定义求欧拉函数

//题目背景：AcWing 873
#include<iostream>
using namespace std;
int main()
{
    int n,a;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d",&a);
        int res=a;
        for(int i=2;i<=a/i;i++)    //分解质因数
        {
            if(a%i==0)
            {
                res=res/i*(i-1);   //先作除法再作乘法，如果先作乘法可能出现中间结果过大而最终结果溢出
                while(a%i==0) a/=i;
            }
        }
        if(a>1) res=res/a*(a-1);//先作除法再作乘法，如果先作乘法可能出现中间结果过大而最终结果溢出
        printf("%d\n",res);
    }
    return 0;
}

筛法求欧拉函数

给定一个正整数$n$，求$1∼n$中每个数的欧拉函数之和。
可利用线性筛法求质数的原理

//题目背景：AcWing 874
#include<iostream>
using namespace std;
const int N=1000010;
int primes[N],cnt;  //存储质数
int eular[N];  //存放每个数的欧拉函数
bool st[N];  //标记是否为质数，true表示不是质数
typedef long long LL;
int main()
{
    int n;
    scanf("%d",&n);
    eular[1]=1;  //1的欧拉函数为1
    for(int i=2;i<=n;i++)
    {
        if(!st[i])
        {
            primes[cnt++]=i;
            eular[i]=i-1;   //质数的欧拉函数为i-1，因为质数n与1~n-1的每个数都互质
        }
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)
            {
                eular[i*primes[j]]=primes[j]*eular[i]; 
                break;
            }
            eular[i*primes[j]]=(primes[j]-1)*eular[i];
        }
    }
    LL res=0;
    for(int i=1;i<=n;i++) res+=eular[i];
    printf("%ld",res);
    return 0;
}

证明：
+ 当i%primes[j]==0

+ 当i%primes[j]！=0

欧拉定理

如果a和m互质，则

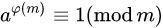
证明

费马小定理：