第21讲 红黑树和并查集
红黑树
简介:是个二叉搜索树。
1.1 定义
(1) 结点是红色或黑色。
(2) 根结点是黑色。
(3) 所有叶子都是黑色。(叶子是NIL空结点,如下图中的,可以理解为一般意义上叶子的空结点 )
.png)
(4) 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
(5) 从任一结点(这里的叶结点也是指空结点)其每个叶子的所有路径都包含相同数目的黑色结点。
1.2 性质
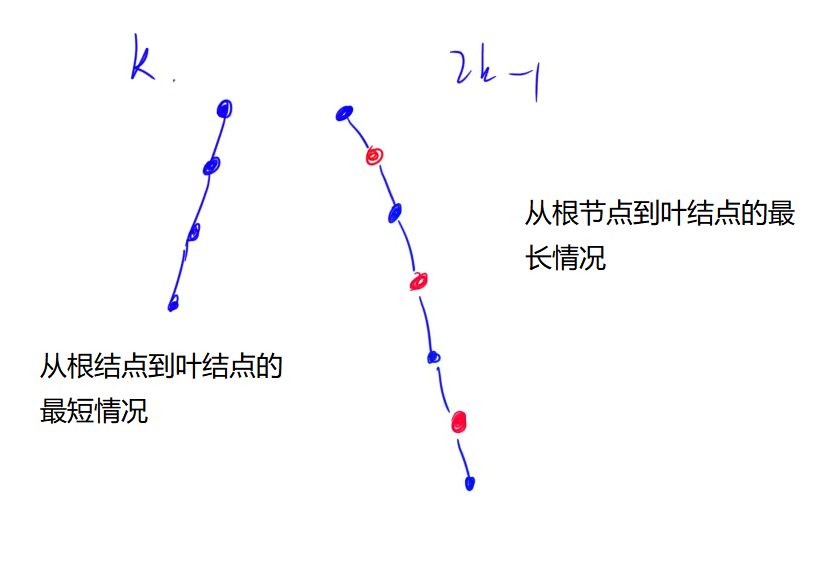
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
1.3 平衡操作(预测是考重点)
1.3.1 插入(跟二叉搜索树的一样)
1.3.1.1 被插入的节点是根节点。
直接把此节点涂为黑色。
1.3.1.2 被插入的节点的父节点是黑色。
什么也不需要做。
1.3.1.3 被插入的节点的父节点是红色。
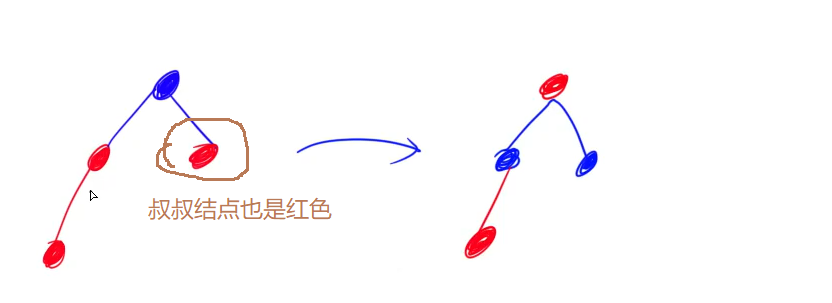
[1] 当前节点的祖父节点的另一个子节点(叔叔节点,也就是插入结点的父结点的兄弟结点)也是红色。
(1) 将“父节点”设为黑色。
(2) 将“叔叔节点”设为黑色。
(3) 将“祖父节点”设为“红色”。
(4) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。
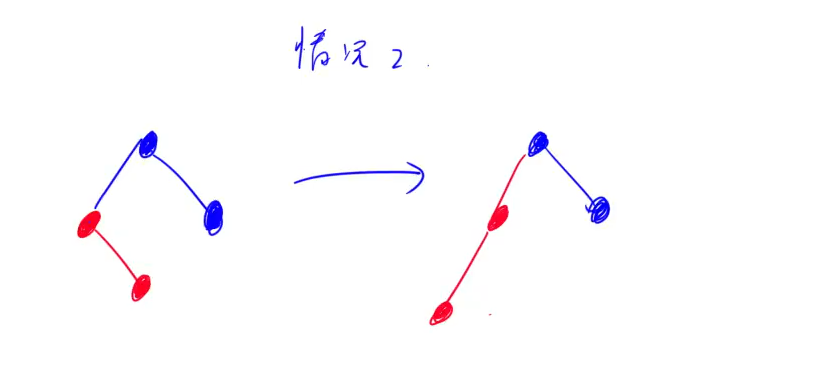
[2] 叔叔节点是黑色,且当前节点是其父节点的右孩子
(1) 将“父节点”作为“新的当前节点”。
(2) 以“新的当前节点”为支点进行左旋。
PS:做完以上操作之后,属于情况3
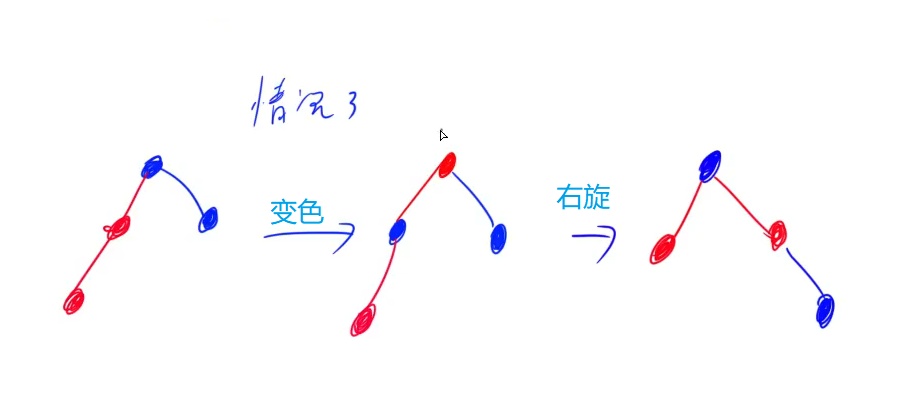
[3] 叔叔节点是黑色,且当前节点是其父节点的左孩子
(1) 将“父节点”设为“黑色”。
(2) 将“祖父节点”设为“红色”。
(3) 以“祖父节点”为支点进行右旋。
总结:第一种情况操作完,并没有完全结束,还需要递归往上进行;第二种情况操作完转化为第三种情况;第三种情况操作完就结束了。
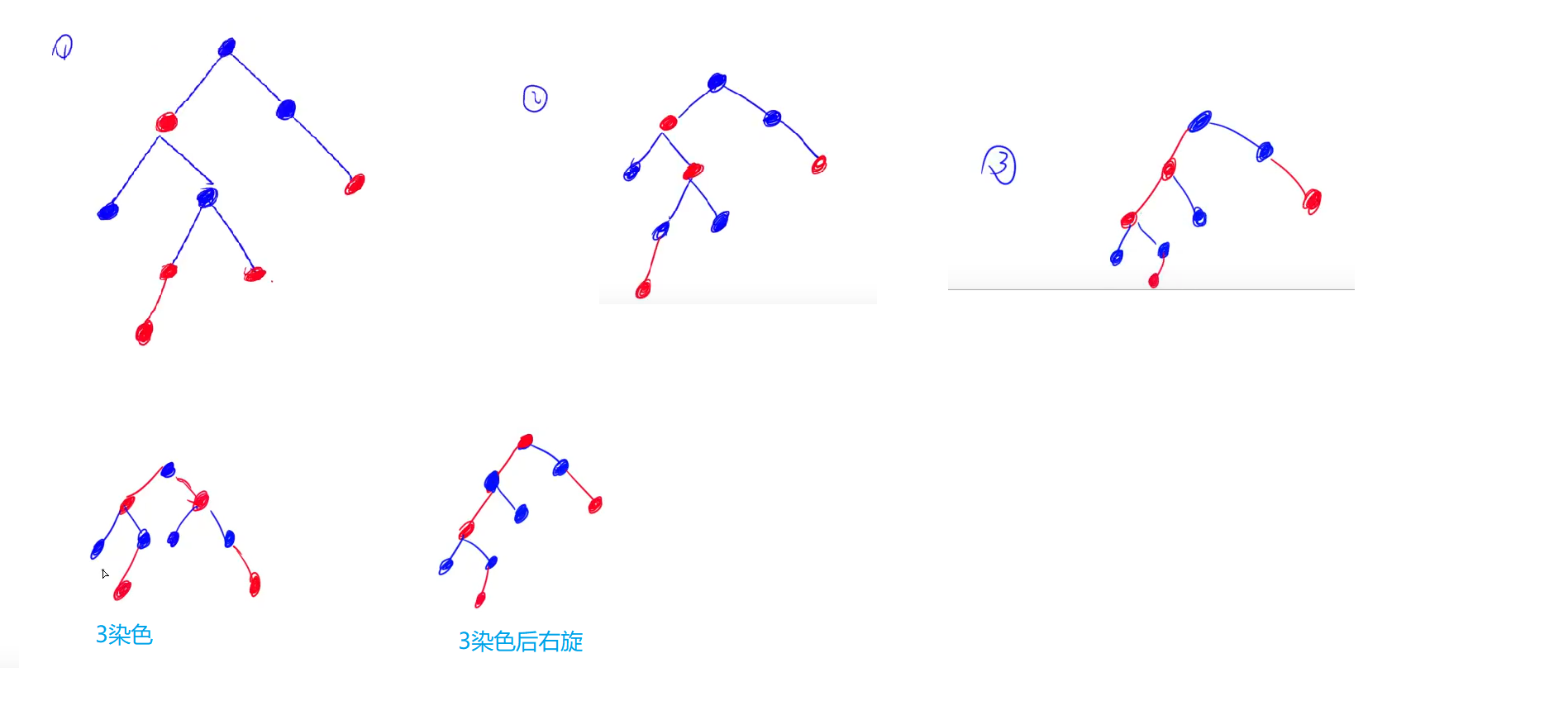
1.3.2 删除

1.3.2.1 x指向一个”红+黑”节点。
将x设为一个”黑”节点即可。
1.3.2.2 x指向根。
将x设为一个”黑”节点即可。
1.3.2.3
[1] x的兄弟节点是红色。
(1) 将x的兄弟节点设为“黑色”。
(2) 将x的父节点设为“红色”。
(3) 对x的父节点进行左旋。
(4) 左旋后,重新设置x的兄弟节点。
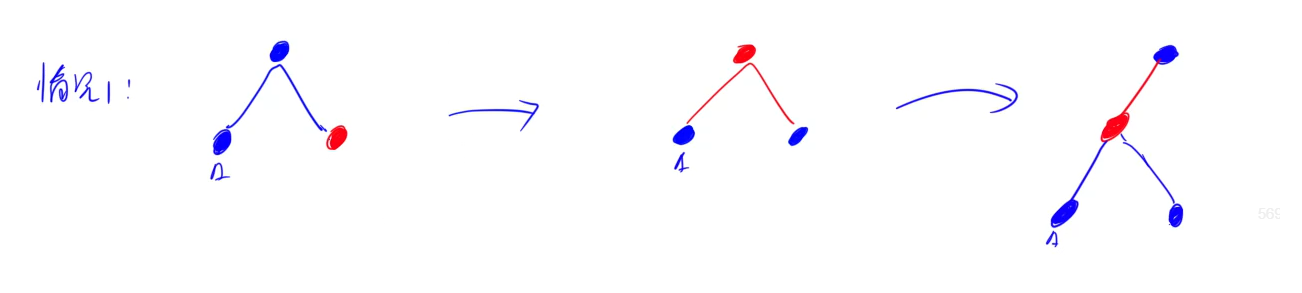
[2] x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。
(1) 将x的兄弟节点设为“红色”。
(2) 设置“x的父节点”为“新的x节点”。

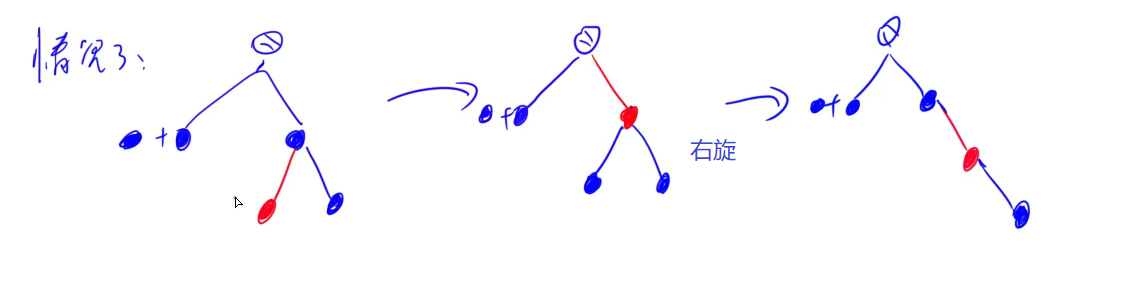
[3] x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。(转换为情况4)
(1) 将x兄弟节点的左孩子设为“黑色”。
(2) 将x兄弟节点设为“红色”。
(3) 对x的兄弟节点进行右旋。
(4) 右旋后,重新设置x的兄弟节点。
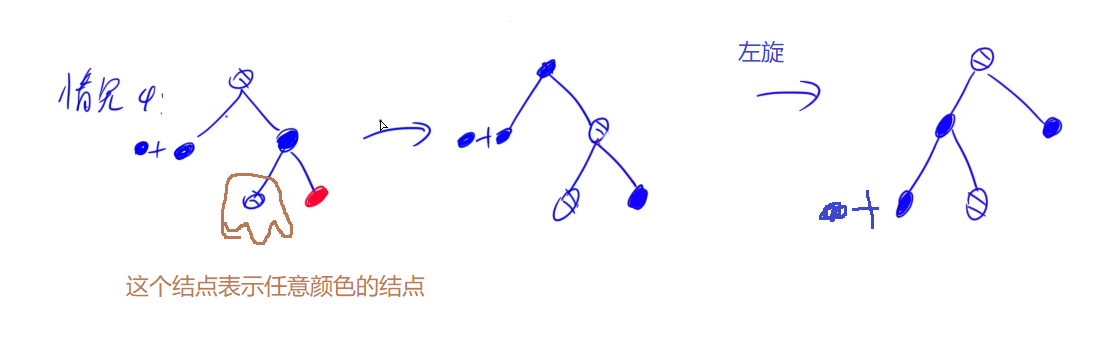
[4] x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。
(1) 将x父节点颜色 赋值给 x的兄弟节点。
(2) 将x父节点设为“黑色”。
(3) 将x兄弟节点的右子节设为“黑色”。
(4) 对x的父节点进行左旋。
总结:
情况一:将兄弟结点变为黑色,转还为情况2、3、4;
情况二:做完之后,还需要再往上继续递归处理(最多logn次)
情况三:转还为情况四
情况四:做完之后就可以直接解决。
时间复杂度:logn
并查集
2.1 定义
用森林维护集合关系,支持合并(两个树合并为一个)、查询(两个元素在同一个树中就是在一个集合中)等操作。
2.2 优化
(1) 路径压缩:因为所有结点只关心自己到根结点,所以从某个结点走向根结点的这一条路径上;我们把这个路径上的每个结点都直接指向根结点(走的时候记录),这样下次再有哪个结点走向根,就不用再走了。
时间复杂度:mlogn(m操作次数,n是操作数量)
(2) 按秩合并:第一种按照树高:将矮树插入到高树中。
第二种按照结点数量:将结点少的树合并到结点数多的树中。

