深度优先搜索 DFS

• 以树的结构去搜索，尽可能往深处搜，搜到叶节点回溯
• 执着的特性：只有在当前节点没有未被搜索过的子节点时才回溯
• 数据结构：栈；空间复杂度：$O(h（深度）)$
  • 优点：空间复杂度低
  • 缺点：不具有最短性
  • 关于递归，dfs与栈：写dfs一般都是递归搜索，不会涉及创建栈。实际上，程序调用函数、创建局部变量就是以栈的形式存储在内存中的
• 在实际问题中应用dfs 回溯 & 剪枝
  • 回溯
    • 首先明确搜索顺序
    • 从根节点开始画搜索树，先向深处画出一条路，到叶节点之后回溯，再向深处画。这样就可以得到dfs搜索树
    • 回溯时注意要恢复现场的问题
    • 典型例题：AcWing 842. 排列数字
      • 
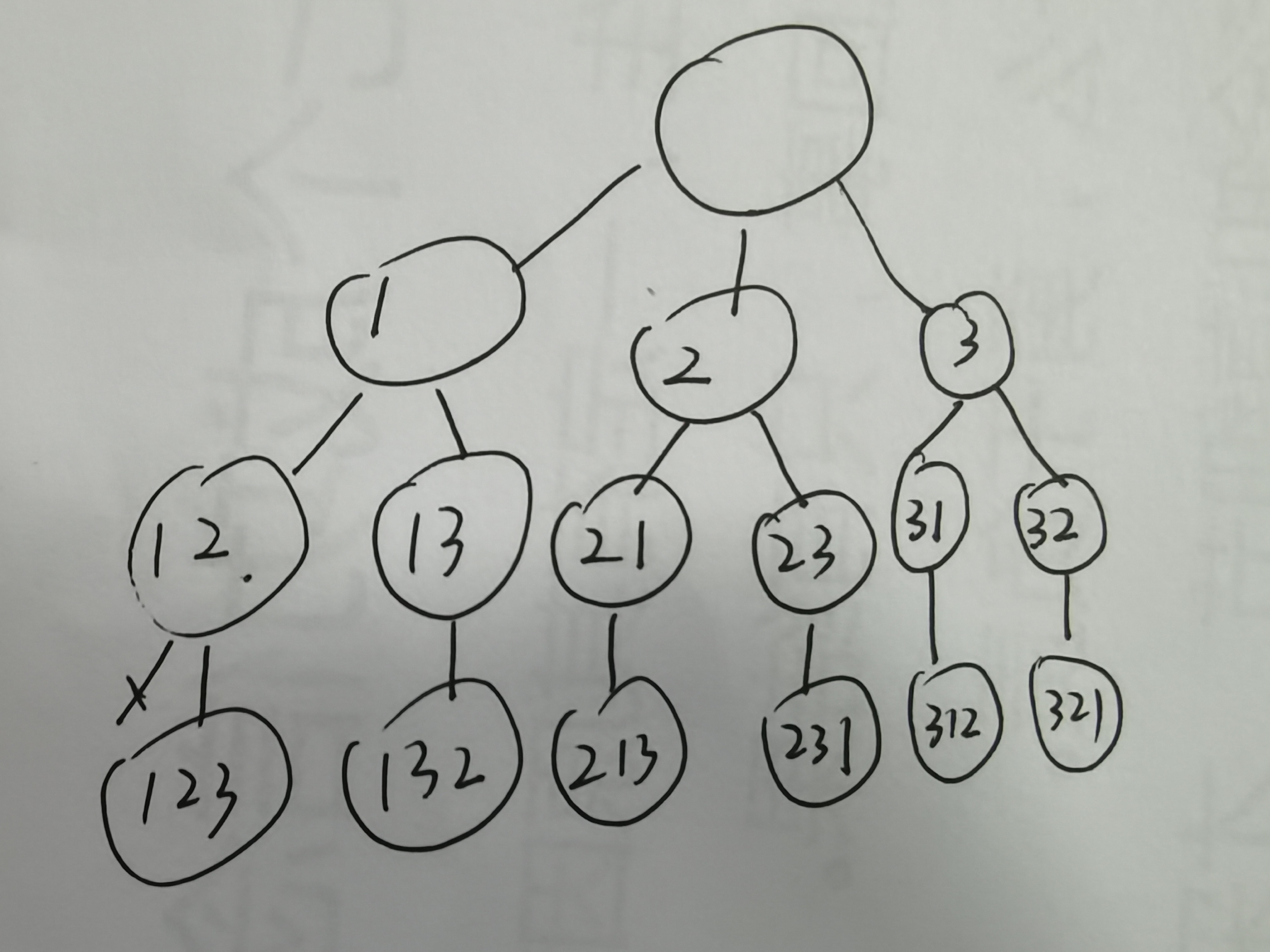
      • 代码加注释
      • 可以看出，dfs把每一个情况都遍历了一遍，所以dfs也称作暴搜
  • 剪枝
    • 当提前判断出当前搜索方案不合法时，直接停止该方案的搜索而转向其他方案的搜索
    • 可以看作是对暴搜的优化
    • 典型例题：AcWing 843. n-皇后问题
      • 这里的遍历类似排列数字，但是每一次遍历都增加了对方案合法性的判断，只有确保当前的搜索是合法时才进行更深的遍历
      • 两种遍历方式
        • 按列（行）顺序遍历
        • 按格子顺序遍历
      • 代码加注释

宽度优先搜索 BFS

• 以树的结构去搜，每次把同一层的点搜索完之后才会向下搜
• 稳重的特性：只有在当前所在层没有未被搜索的点时才向下搜索
• 数据结构：队列；空间复杂度：$O(2^h)$
  • 优点：搜索具有最短性
  • 缺点：空间复杂度大
  • 局限性：只有在边权重均为1时得到的答案才是最短路
• 框架

queue <- 初始情况
while !queue.empty
{
    t = queue[hh ++];
    拓展t,直到t全部搜完
}

• 实际问题：
  • AcWing 844. 走迷宫
  • AcWing 845. 八数码
  • 在解决问题时还要考虑，queue中存储的实际上是问题方案的一种状态。这种状态用什么数据结构去表示，距离用什么数据结构去存储，都是要具体分析的

树与图的存储

树是一种特殊的图（无环连通图），与图的存储方式相同。

有向图的边 ab ,存储 a -> b
对于无向图中的边 ab，存储两条有向边 a->b, b->a。

因此我们可以只考虑有向图的存储。

(1) 邻接矩阵：g[a][b] 存储边 a->b
- 如果有重边就存储权重最小的一条边
- 空间复杂度 $O(n^2)$ ,较大，一般用于存稠密图($m=n^2$)

(2) 邻接表：

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;             //存储形式和哈希表的拉链法是一样的

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);                //一定不要忘记初始化，否则会TLE

树与图的遍历

时间复杂度 $O(n+m)$, $n$ 表示点数，$m$ 表示边数

(1) 深度优先遍历 —— 模板题 AcWing 846. 树的重心

int dfs(int u)
{
        st[u] = true; // st[u] 表示点u已经被遍历过

        for (int i = h[u]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (!st[j]) dfs(j);
        }
}

• 代码加注释

(2) 宽度优先遍历 —— 模板题 AcWing 847. 图中点的层次

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
        int t = q.front();
        q.pop();

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (!st[j])
            {
                st[j] = true; // 表示点j已经被遍历过
                q.push(j);
            }
        }
}

• 代码加注释

拓扑排序 —— 模板题 AcWing 848. 有向图的拓扑序列

时间复杂度 $O(n+m)$, $n$ 表示点数，$m$ 表示边数

• 定义：若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。
• 有向图才有拓扑序列
• 有环的图一定没有拓扑序；
• 有向无环图一定具有拓扑序列，因此有向无环图也被成为拓扑图
• 出度 & 入度
  • 出度：指向其他点的边数
  • 入度：指向自己的边数
  • 证明：一个有限的有向无环图一定存在至少一个入度为0的点；
    • 反证法，每一个点都可以找到被邻接的点，一直沿着路径找到第 $n+1$ 个点时,由于图中只有 $n$ 个点，因此路径中一定有两个点相同，因此路径中一定有环，与无环矛盾。综上，结论成立
• 由度数分析拓扑序
  • 对于入度为0的点，由于没有点指向它，它放在队头
  • 从入度为0的点开始进行bfs

bool topsort()
{
        int hh = 0, tt = -1;

        // d[i] 存储点i的入度
        for (int i = 1; i <= n; i ++ )
            if (!d[i])
                q[ ++ tt] = i;

        while (hh <= tt)
        {
            int t = q[hh ++ ];

            for (int i = h[t]; i != -1; i = ne[i])
            {
                int j = e[i];
                if (-- d[j] == 0)
                    q[ ++ tt] = j;
            }
        }

        // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
        return tt == n - 1;
}

/*
这里模板用的是数组模拟队列而不是stl队列，因为模拟队列的数组存储的恰好是图的一种拓扑排序，
因此可以直接作为答案输出；如果用stl则需要另开一个数组来存拓扑排序，反而显得画蛇添足
*/

• 代码加注释

作者：yxc
链接：https://www.acwing.com/blog/content/405/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。