dijkstra
小明上学的时候,从家到学校的道路非常多,小明为了减少路上骑车的时间,因此,想找出一个最短的路径。他构造一个网络图,如下:
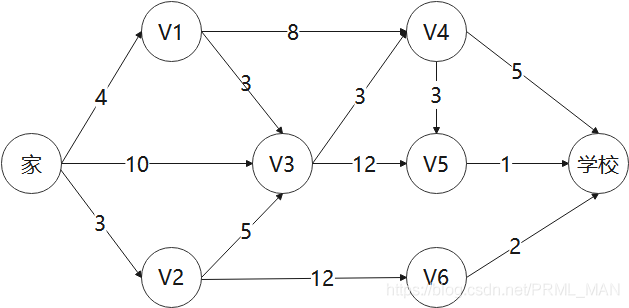
1)所有的点到家的距离都进行初始化:
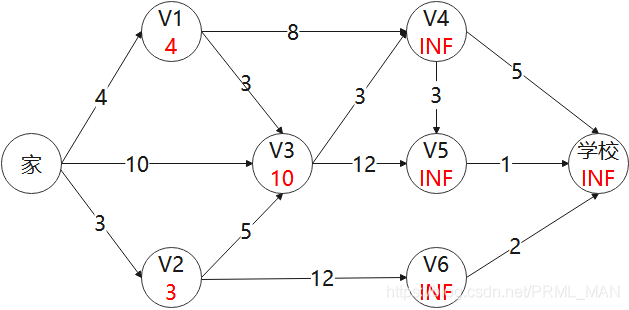
2)每次选择距离家最短的一个点,然后用这个点的距离更新其他相邻点到家的距离,如果比当前的点小,则更新节点的值。查看所有点,V2距离家最近,则用V2更新与它相邻的点
V3: MIN(10, 3 + 5) = 8
V6: MIN(3 + 12, INF) = 15
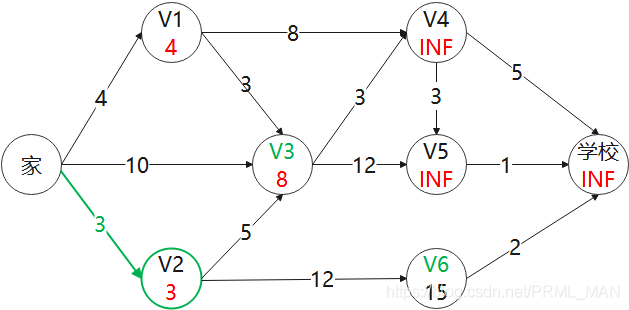
3) 剔除掉V2这个点(进行标记),然后从所有点中找距离家最小值的点,发现V1最小,更新V1相连的点 V3, V4
V3: MIN(8, 4+3) = 7
V4: MIN(4+8, INF) = 12
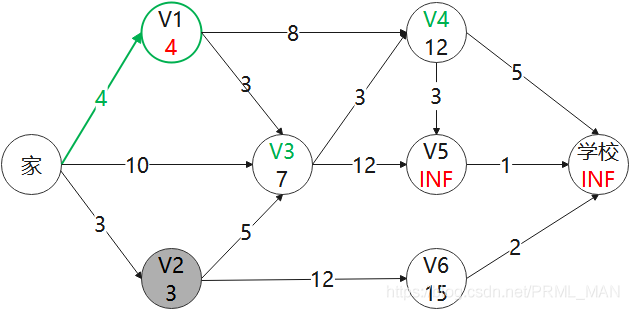
4)剔除掉V1这个点,继续找最小值的点 V3,更新V3相连的点 V4 V5
V4: MIN(12, 10) = 10
V5: MIN(7 + 12, INF) = 19
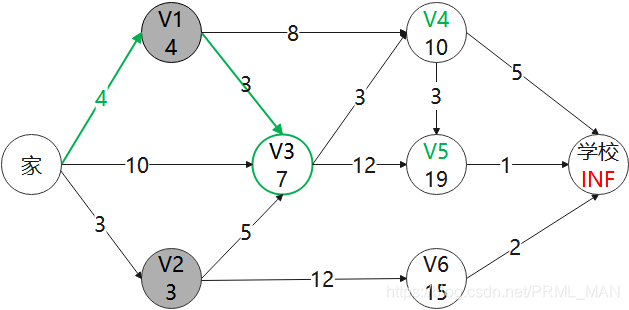
5)剔除掉V3这个点,继续找最小值的点 V4,更新V4相连的点 学校和 V5
学校: MIN(10+5, INF) = 15
V5: MIN(19, 10+3) = 13
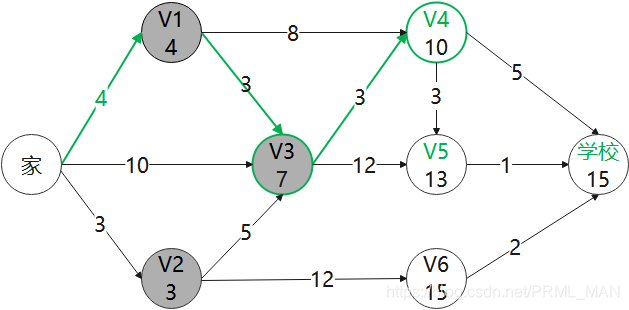
6)剔除掉V4这个点,继续找最小值的点 V5,更新V5相连的点 学校
学校: MIN(15, 13+1) = 14
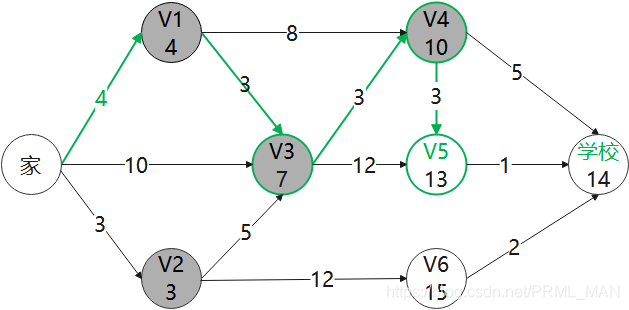
6)剔除掉V5这个点,继续找最小值的点 学校,更新学校相连的点 NULL。
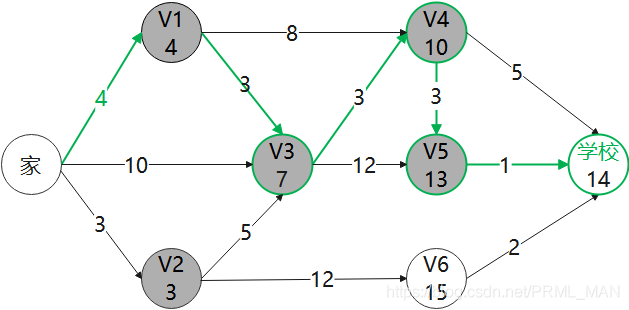
到目前为止,小明找打了从家到学校的最短距离为14,经过的路径为:家-V1-V3-V4-V5-学校。
上面的整个流程就是dijkstra算法的核心思想
## Dijkstra求最短路 I(未优化)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //用于记录该点的最短距离是否已经确定
int n,m;
int Dijkstra()
{
memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无限大
dist[1]=0; //第一个点到自身的距离为0
//每次第一步先找最小值,
for(int i=1;i<=n;i++) //有n个点所以要进行n次 迭代
{
int t=-1; //t存储当前访问的点
//找没有被标记的点当中dist最小的
for(int j=1;j<=n;j++) //这里的j代表的是从1号点开始
if(!st[j]&&(t==-1||dist[t]>dist[j]))
//遍历 dist 数组,找到没有确定最短路径的节点中距离源点最近的点t
t=j;
st[t]=true; //这个点已经标记
for(int j=1;j<=n;j++) //依次更新每个点所到相邻的点路径值
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
if(dist[n]==0x3f3f3f3f) return -1; //如果第n个点路径为无穷大即不存在最低路径
return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g); //初始化图 因为是求最短路径
//所以每个点初始为无限大
while(m--)
{
int x,y,z;
cin>>x>>y>>z;
g[x][y]=min(g[x][y],z); //如果发生重边的情况则保留最短的一条边
}
cout<<Dijkstra()<<endl;
return 0;
}
## Dijkstra求最短路 II(小根堆优化)
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;//first存储到起始点距离,second存储编号
//稠密图指的是边的条数|E|接近于|V|²(|V|是点集数),稀疏图是指边的条数|E远小于于|V|²(数量级差很多)
int h[N],w[N],e[N],ne[N],idx;//稀疏图用邻接表存,h[]是表头,w[]是权重,h[],ne[]所表示的值是下标,e[]表示的是数
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //用于记录该点的最短距离是否已经确定
int n,m;
void add(int a,int b,int c){//加入有向边a到b,权值为c
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void Dijkstra()
{
memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无限大
dist[1]=0; //第一个点到自身的距离为0
//每次第一步先找最小值,
priority_queue<PII,vector <PII>,greater <PII>> heap;
heap.push({0,1});//相当于初始化dist[1]=0,first是每个点到起始点的距离,seconnd是每个点的编号
while (heap.size())
{
auto t = heap.top();//取距离起始点最近的点
heap.pop();
int ver = t.second, distance = t.first;//ver:节点编号,distance:距离ver 的距离
if (st[ver]) continue;//如果已经被标记,则跳过该点
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});//距离变小,则入堆
}
}
}
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);//初始表头为-1
while(m--)
{
int x,y,z;
cin>>x>>y>>z;
add(x,y,z);//邻接表会自动处理重边,无需多管
}
Dijkstra();
if(dist[n]==0x3f3f3f3f) cout<<"-1"; //如果第n个点路径为无穷大即不存在最低路径
else cout<<dist[n];
return 0;
}
## bellman_ford求有边数限制的最短路
/*对于back[]备份的解释:
每次迭代,是从当前状态每个节点距离d[i] = min(d[i],last[j] + g[j][i])试图添加“一条”路径,
来得到k步以内的最短距离,每次迭代只向前迈一步。
第k次迭代,是从第k-1步的状态,转移向k步状态。
而串联指的是,在第k次迭代中途,d[]中部分数据已经发生了迭代,得到的结果是k条边的最短路径,
在后续中再次对其判断迭代后,得到了k+1条边时才能得到的距离,在一次迭代中添加了多条边。
对于获得最短路径的最终状态来说,串联没有影响。
而对于有边数限制的最短路来说,串联会导致得到的结果是不符合要求的,超过边数限制的最短路。
*/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 10010;
struct Edge{//bellmax_ford算法村边用结构体
int a;
int b;
int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边
void bellman_ford() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i++) {//k次循环
memcpy(back, dist, sizeof dist);//back数组存储上一次迭代的结果,这样不会发生串联
//防止串联更新,导致第k层循环之后找到一个边数大于k的路径
for (int j = 0; j < m; j++) {//遍历所有边
int a = e[j].a, b = e[j].b, w = e[j].w;
dist[b] = min(dist[b], back[a] + w);
//使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
}
}
if (dist[n] > 0x3f3f3f3f / 2) cout<<"impossible";//为什么不写dist[n]==0x3f3f3f3f呢?
//是因为存在负权边,对于正无穷,加上这个负权边的权值后,边所指向的那个点会小于负无穷,
//但又不会小太多,最多减去500*10000,所以只要大于0x3f3f3f3f/2,即可
else cout<<dist[n];
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
e[i] = {a, b, w};
}
bellman_ford();
return 0;
}
## spfa求最短路
/*
对于dist[b]=min(dist[b],dist[a]+w);当且仅当dist[a]变小了,dist[b]才会变小(w是定值)
先把起点放入队列
队列中存所有变小的那些点,只要队列中还有点变小,就执行迭代:
1.t=q.front(),q.pop();
2.更新所有节点t指向的点,然后只要这个点没有被放入队列中,就将其放入队列
*/
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];//判断这个点是不是再队列当中
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int t = spfa();
if (t == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", t);
return 0;
}
## spfa判断负环
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int w[N];
int dist[N], cnt[N];
//cnt记录每个点到起点的边数,当cnt[i] >= n 表示出现了边数>=结点数,必然有环,而且一定是负环!
bool st[N];
//判断当前的点是否已经加入到队列当中了;已经加入队列的结点就不需要反复的把该点加入到队列中了
//就算此次还是会更新到起点的距离,那只用更新一下数值而不用加入到队列当中。
//意味着,st数组起着提高效率的作用,不在乎效率的话,去掉也可以
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa()
{
//初始化所有非起点和起点的距离
// memset(dist, 0x3f, sizeof dist);
// dist[1] = 0;
// 这里不需要初始化dist数组为 正无穷。不用初始化的原因是, 如果存在负环,
//那么dist不管初始化为多少, 都会被更新
//定义队列,起点进队, 标记进队
queue<int> q;
for (int i = 1; i <= n; i ++ ){
//判断负环,只从起点出发,有可能到达不了负环那里,需要一开始就把所有结点放入队列,
//且标记进入了队列降低效率
q.push(i);
st[i] = true;
}
//队列中的点用来更新其他点到起点的距离
while (q.size()){
//取队头,弹队头
auto t = q.front();
q.pop();
//t出队,标记出队
st[t] = false;
//更新与t邻接的边
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];//结点j可以通过中间点t降低距离
cnt[j] = cnt[t] + 1;//那么结点j在中间点t的基础上加一条到自己的边
if (cnt[j] >= n) return true;//边数不小于结点数,出现负环,函数结束
if (!st[j])
//若此时j没在队列中,则进队。已经在队列中了,上面已经更新了数值。重复加入队列降低效率
{
//j进队,标记进队
q.push(j);
st[j] = true;
}
}
}
}
return false;//走到这了,函数还没结束,意味着边数一直小于结点数,不存在负环
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
if (spfa()) puts("Yes");
else puts("No");
return 0;
}
floyd求最短路
/*
状态:d[k][i][j]表示“经过若干个编号不超过k的节点”从i到j的最短路长度。
不妨这样理解:
“只能使用第1号到第k号点作为中间媒介时,点i到点j之间的最短路径长度。”
图中共有n个点,标号从1开始到n。因此,在这里,k可以认为是动态规划算法在进行时的一种层次,或者称为“松弛操作”。d[1][i][j]表示只使用1号点作为中间媒介时,点i到点j之间的最短路径长度;d[2][i][j]表示使用1号点到2号点中的所有点作为中间媒介时,点i到点j之间的最短路径长度;d[n-1][i][j]表示使用1号点到(n-1)号点中的所有点作为中间媒介时,点i到点j之间的最短路径长度d[n][i][j]表示使用1号到n号点时,点i到点j之间的最短路径长度。有了状态的定义之后,就可以根据动态规划思想来构建动态转移方程。
动态转移的基本思想可以认为是建立起某一状态和之前状态的一种转移表示。按照前面的定义,d[k][i][j]是一种使用1号到k号点的状态,可以想办法把这个状态通过动态转移,规约到使用1号到(k-1)号的状态,即d[k-1][i][j]。对于d[k][i][j](即使用1号到k号点中的所有点作为中间媒介时,i和j之间的最短路径),可以分为两种情况:(1)i到j的最短路不经过k;(2)i到j的最短路经过了k。不经过点k的最短路情况下,d[k][i][j]=d[k-1][i][j]。经过点k的最短路情况下,d[k][i][j]=d[k-1][i][k]+d[k-1][k][j]。因此,综合上述两种情况,便可以得到Floyd算法的动态转移方程:
d[k][i][j]=min(d[k-1)[i][j],d[k-1][i][k]+d[k-1][k][j])
最后,d[n][i][j]就是所要求的图中所有的两点之间的最短路径的长度。在这里,需要注意上述动态转移方程的初始(边界)条件,即d[0][i][j]=w(i, j),也就是说在不使用任何点的情况下(“松弛操作”的最初),两点之间最短路径的长度就是两点之间边的权值(若两点之间没有边,则权值为INF,且我比较偏向在Floyd算法中把图用邻接矩阵的数据结构来表示,因为便于操作)。当然,还有d[i][i]=0(i∈[1,n])。

感觉非常像区间dp
与背包问题一样,可以发现每一个第k阶段的状态(d[k][i][j]),所依赖的都是前一阶段(即第k-1阶段)的状态(如d[k-1][i][j],d[k-1][i][k]和d[k-1][k][j]),所以k这一维可被省略,使用滚动数组
即:当外层循环k刚开始是,d[i][j]保存着“经过编号不超过k-1的节点”从i到j的最短路长度。
//邻接矩阵,三重循环完之后表示从i到j的最短路径长度
*/
#include <iostream>
#include<cstdio>
using namespace std;
const int N = 210,INF=1e9;
int d[N][N];
int n, m, k;
void floyd(){
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main(){
scanf("%d%d%d", &n, &m, &k);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(i==j) d[i][j]=0;//存在自环
else d[i][j]=INF;
}
while(m--){
int a, b,w;
scanf("%d%d%d", &a, &b,&w);
d[a][b]=min(d[a][b],w);//又重边,只要最小边
}
floyd();
while(k--){
int a,b;
scanf("%d%d",&a,&b);
if(d[a][b]>INF/2) puts("impossible");//存在负权边,比INF小
else printf("%d\n",d[a][b]);
}
return 0;
}

