【2021】 CSP - S 题解
这是一篇迟来的题解,承载着一份未到的喜悦。
伴随着新年将至的钟声,揭开的是旧年里的酸酸甜甜、挫折成长。
在这一年里,
或是幸运,我能够接触到信息学、有了一番不同的梦想;或是不幸,我在自鸣得意时跌入谷底,灾难重重。
T1 廊桥分配 - 困难
算法一
(平衡树) O(nlog(n))
这是一道非常有趣的题目,反正当时一眼看去就是个三分,然后样例全过,fst 了不少。
因为国内航班飞机和国际航班飞机 不能停靠在 同一个区。
这就导致了状态 可能性变数过大,从而增加了枚举的难度,
如果是按照朴素方法枚举,复杂度会达到 O(n2logn),太大了,那该怎么办呢?
由于这道题不满足 凸函数 性质,非严格单调。
所以不能用三分来优化时间复杂度。
在这种情况下,一般的,能想到如果 不能直接找到 要怎么分配,可不可以先预处理,再一一判断。
显然的,如果 分别预处理 两种飞机的停靠,是满足 单调性质 的,那么,就可以做一些其它的考量。
想要快速处理将飞机停靠在 不同数量的廊桥上 所容纳的飞机,就不要去重复处理同一件事。
这一点,可以用 前缀和 解决。
那我们就需要一个能够在 logn 的时间内查找飞机 离开时间 的算法。
这样的算法往往有两种选择 优先队列 或 平衡树。
但是,这不仅仅是要查找 最晚离开时间,还要具有删除功能。
这需要用到 懒惰删除法,这里是直接用 set 解决。
#include <bits/stdc++.h>
#define x first
#define y second
#define For(i, j, k) for (int i = j; i <= k; i ++ )
using namespace std;
const int N = 100010, INF = N;
typedef pair<int, int> PII;
int ans;
int n, m1, m2;
PII a[N];
PII b[N];
set<PII> A, B;
set<PII>::iterator id;
int num1[N], num2[N];
int add(set<PII> &S)
{
int res = 0, now = 0;
For(i,0,INF)
{
id = S.lower_bound({now, now}); // 寻找进入机场的飞机在上一架飞机离开后最早的一个, 返回迭代器
if (id == S.end()) break; // 退出
res ++, now = (*id).y;
S.erase(id);
}
return res;
}
int main()
{
scanf("%d %d %d", &n, &m1, &m2);
For(i, 1, m1) scanf("%d %d", &a[i].x, &a[i].y);
For(i, 1, m2) scanf("%d %d", &b[i].x, &b[i].y);
For(i, 1, m1) A.insert(a[i]);
For(i, 1, m2) B.insert(b[i]);
For(i, 1, n) num1[i] = num1[i - 1] + add(A);
For(i, 1, n) num2[i] = num2[i - 1] + add(B);
For(i, 0, n) ans = max(ans, num1[i] + num2[n - i]);
printf("%d", ans);
return 0;
}
T2 括号序列 - 困难
这应该是我遇到的最难的一道和括号有关的题了。
算法1
(暴力搜索) O(n3n)
遇事不决,先打暴力。
枚举每一个 ? 的三种可能情况,最后判断是否满足要求。
即,相邻的 * 不能超过 k 个,不能出现 (*A*) 、A* 或 *A,后两种只有开头或结尾可能出现。
期望得分:15 分
#include <bits/stdc++.h>
#pragma GCC optimize(3)
#define q(t) q.top()
using namespace std;
const int N = 510, mod = 1e9 + 7;
int n, k, ans;
int num[N], t;
int f[N];
char a[N];
int check()
{
stack<int> q;
for (int i = 0, c = 0; i < n; i ++ )
{
if (a[i] == '*')
{
f[i] ++;
if (++ c > k) return 1;
}
else c = 0;
f[i + 1] = f[i];
}
if (a[0] == '*' || a[n - 1] == '*') return 2;
for (int i = 0; i < n; i ++ )
{
if (a[i] == '(') q.push(i);
if (a[i] == ')')
{
if (q.empty()) return 2;
if (a[q(t) + 1] == '*' && a[i - 1] == '*')
{
if (f[i - 1] - f[q(t)] != i - 1 - q(t))
return 2;
}
q.pop();
}
}
return q.size() ? 2 : 0;
}
void dfs(int u)
{
if (u >= t) {
if (!check()) ans ++;
return;
}
a[num[u]] = '(';
dfs(u + 1);
a[num[u]] = ')';
dfs(u + 1);
a[num[u]] = '*';
dfs(u + 1);
}
int main()
{
scanf("%d %d\n%s", &n, &k, a);
for (int i = 0; i < n; i ++ )
if (a[i] == '?')
{
num[t ++ ] = i;
}
if (check() != 1) dfs(0);
printf("%d", ans % mod);
}
算法二
(区间 Dp) O(n3)
题目背景
一个长度为 n 且符合规范的括号序列,其有些位置已经确定了,有些位置尚未确定,求这样的括号序列一共有多少个。
分析
对于蒟蒻的博主而言,这道题的难度显然是犯规了的,但是,如果你能合理运用题目的条件,倒也能出奇制胜。
既然这道题写不出来,那就先看一下它的 弱化版。
通常对于一个求方案数的题目,只有两种算法可以解决,DFS 和 Dp。
这道题数据量很大,那就只有可能是选 Dp 了,那到底可以用哪种 Dp 呢?
状压不行,数据量太大了,背包、树形、数位 似乎也不行。
不过,好像 状态机 跟这个有点关联,毕竟都有 多个状态 嘛,
这时,请注意一下 括号序列 的性质,多个 合法序列 正确组成的序列也是一个 合法序列。
到这里,答案已经呼之欲出了,没错 状态机思想 + 区间Dp。
所遇困境(以下分析都和弱化版无关)
但是不同的形态可能会有不同的转移,如:(S) 这种只能从 S 转移过来等等。所以只开两维的 f 数组必然是不够的。
更何况 ? 似乎也没有办法处理?(事实上,只能先将它看成 万能牌 ,不再单独考虑。)
思考一下,既然这道题的状态太多了,那为何不能多开一维,用 状态机 的方式,将不同连边的状态 转换。
那我们还剩两个任务,设计状态、状态转移。
设计状态
我们可以发现,对于一个超级括号序列,一定可以表示成以下 七种形式:
() 、(S) 、(AS) 、(SA) 、(A) 、AB 、ASB。
而这 七种形式 又可以分成两类:
包在括号内的:() 、(S) 、(AS) 、(SA) 、(A)
首尾有两个括号序列的:AB 、ASB
我们先尝试多开两位,用 f[i][j][0] 和 f[i][j][1] 分别表示上面这两类情况。
根据题意,(S) 、(AS) 、(SA) 、(A) 都是超级序列,所以我们要用 S 、 AS 、SA 、A 来对第一种情况的超级序列进行转移。
其中 A 满足第一类的要求,但是 S 、AS 、SA 显然都不符合,
因为它们代表三种不同的情况,所以需要再设计三种不同的状态来表示。
所有状态如下:
-
fi,j,0 : 形态如
(...)的括号序列(即左右直接被括号包裹且最左边括号与最右边的括号相互匹配)。 -
fi,j,1 : 形态如
(...)***(...)*(...)的括号序列(即左边以括号序列开头,右边以括号序列结尾)。 -
fi,j,2 : 形态如
***...*的括号序列(即全部是*,记得判断一下两端距离是否不大于 k)。 -
fi,j,3 : 形态如
(...)**(...)***的括号序列(即左边以括号序列开头,右边以*结尾)。 -
fi,j,4 : 形态如
***(...)**(...)的括号序列(即左边以*开头,右边以括号序列结尾)。
状态转移
请见代码(感觉会清晰一点)
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 510, mod = 1e9 + 7;
int n, k;
int f[N][N][5];
char s[N];
bool check(int l, int r)
{
return (s[l] == '(' || s[l] == '?') && (s[r] == ')' || s[r] == '?');
}
signed main()
{
scanf("%lld %lld %s", &n, &k, s + 1); // s 下标从 1 开始
for (int i = 1; i <= n; i ++ ) f[i][i - 1][2] = 1;
for (int len = 1; len <= n; len ++ )
for (int l = 1, r; (r = l + len - 1) <= n; l ++ )
{
f[l][r][2] = f[l][r - 1][2] & (s[r] == '*' || s[r] == '?') & (len <= k);
// 需满足仅由*构成且不超过k个, 因为*都是一样的, 所以值只存在1和0两种可能
if (len == 1) continue; // 当len等于1时, 除f[l][r][2]以外的都只能为0
f[l][r][0] = check(l, r) * (f[l + 1][r - 1][0] + f[l + 1][r - 1][1] + f[l + 1][r - 1][2] + f[l + 1][r - 1][3] + f[l + 1][r - 1][4]) % mod;
// 如果s[l]和s[r]可以组成一个括号的话
for (int k = l; k < r; k ++ ) // 分成[l, k]和[k + 1, r]
{
// AS -> ASB / A + S
f[l][r][3] = (f[l][r][3] + (f[l][k][0] + f[l][k][1]) * f[k + 1][r][2]) % mod;
// f[l][k][0] 和 f[l][k][1] 之间,只有一个是有效的。
// 由乘法原理可知, AS 方案数 = A 方案数 * S 方案数, 总方案数需要累计
// SA -> S + ASB / A
f[l][r][4] = (f[l][r][4] + (f[k + 1][r][0] + f[k + 1][r][1]) * f[l][k][2]) % mod;
// f[k + 1][r][0] 和 f[k + 1][r][1] 之间,只有一个是有效的。
// 由乘法原理可知, SA 方案数 = A 方案数 * S 方案数, 总方案数需要累计
// AB/ASB -> ASB / A / AS + A
f[l][r][1] = (f[l][r][1] + (f[l][k][0] + f[l][k][1] + f[l][k][3]) * f[k + 1][r][0]) % mod;
// 由乘法原理可知, AB 方案数 = A 方案数 * B 方案数, 总方案数需要累计
// 由乘法原理可知, ASB 方案数 = AS 方案数 * B 方案数, 总方案数需要累计
}
}
printf("%lld", (f[1][n][0] + f[1][n][1]) % mod); // 任选一个
}
T3 回文 - 困难
算法一
(贪心) O(n)
本题的数据偏大,只能用 O(n) 或 O(nlogn) 的算法。
同时,本题要求最小字典序,这提醒了我们往贪心这一方面想。
因为答案要的是 回文串,可见对于任意一个字符,若它 第一个 取出,则另一个值相等的字符要 最后取。
根据要 最后取 的字符做 分割线,将这一串数字被分成了两部分(A 和 B),靠左的只能往左取、靠右的往右。
最后就是顺序问题了,因为最终要形成 回文串,这启发我们定义两个指针,从两端往中间搜。
贪心
若 A 队头 等于 A 队尾,因为 A 队队尾后没有 A 队元素,不会产生影响,所以 可以取出。
若 B 队头 等于 B 队尾,因为 B 队队尾后没有 B 队元素,不会产生影响,所以 可以取出。
若 A 队头 等于 A 队中的元素,因为 A 队中此元素为 局部最晚弹出,其后元素只能往右弹,但右边有分割线,无法也最好不这么弹,所以 不能取出。
若 B 队头 等于 B 队中的元素,因为 B 队中此元素为 局部最晚弹出,其后元素只能往左弹,但左边有分割线,无法弹出,所以 不能取出。
若 A 队头 等于 B 队尾,因为 B 队队尾后没有 B 队元素,不会产生影响,所以 可以取出。
若 B 队头 等于 A 队尾,因为 A 队队尾后没有 A 队元素,不会产生影响,所以 可以取出。
若 A 队头 等于 B 队中的元素,因为 B 队中此元素为 局部最晚弹出,其后元素只能往左弹,但左边有分割线,无法弹出,所以 不能取出。
若 B 队头 等于 A 队中的元素,因为 A 队中此元素为 局部最晚弹出,其后元素只能往右弹,但右边有分割线,无法也最好不这么弹,所以 不能取出。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int T, n;
int a[N], b[N];
int Al, Ar, Bl, Br;
char ans[N];
bool F1, F2;
deque<int> A, B;
void print()
{
for (int i = 1; i <= 2 * n; i ++ ) printf("%c", ans[i]);
puts("");
}
int find(int x)
{
for (int i = 2; i <= 2 * n; i ++ )
if (a[i] == x)
{
return i;
}
}
void build(bool op, int S, int E)
{
A.clear(), B.clear();
if(!op) Al = 1, Ar = E, Bl = E + 1, Br = 2 * n;
if (op) Al = 1, Ar = S, Bl = S + 1, Br = 2 * n;
for (int i = Al; i <= Ar; i ++ ) A.push_back(a[i]);
for (int i = Bl; i <= Br; i ++ ) B.push_back(a[i]);
}
bool work()
{
int L = 1, R = n * 2;
while (A.size() || B.size())
{
// 两个元素都在 A 栈里, 其中一个在队首, 出栈操作为 'L'
// 另一个元素会是此栈中最晚出栈的, 因为A栈原队尾是全局最晚出栈的
// 所以最好也只能选 'L'
if (A.size() >= 2 && A.front() == A.back())
{
A.pop_front(), A.pop_back();
ans[L] = 'L', ans[R] = 'L';
L ++, R --;
}
else if (A.size() && B.size() && A.front() == B.front())
{
A.pop_front(), B.pop_front();
ans[L] = 'L', ans[R] = 'R';
L ++, R --;
}
// 两个元素都在 B 栈里, 其中一个在 B 栈队尾, 出栈操作为 'R'
// 另一个元素会是当前栈中最晚出栈的, 因为A栈原队尾是全局最晚出栈的
// 所以只能选 'R'
else if (B.size() >= 2 && B.front() == B.back())
{
B.pop_front(), B.pop_back();
ans[L] = 'R', ans[R] = 'R';
L ++, R --;
}
else if (A.size() && B.size() && A.back() == B.back())
{
A.pop_back(), B.pop_back();
ans[L] = 'R', ans[R] = 'L';
L ++, R --;
}
else return false;
}
print();
return true;
}
int main()
{
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n);
for (int i = 1; i <= 2 * n; i ++ ) scanf("%d", &a[i]);
F1 = false, F2 = false;
int Ls = 1;
int Le = find(a[Ls]);
strcpy(ans, "");
build(0, Ls, Le);
if (work()) continue;
int Re = 2 * n;
int Rs = find(a[Re]);
strcpy(ans, "");
build(1, Rs, Re);
if (work()) continue;
puts("-1");
}
return 0;
}
T4 交通规划 - 困难
前言
考场上想到了 45 分暴力的写法,但码力太蒻了,最后没有调出来。
题面简述
给定一个网络和 T 次询问,每次询问给出 k 个附加点的相邻点,
附加点都在 网格边缘以外,并和边缘的一个节点相连,给出其 边权 和附加点的 颜色。
求线段上 端点异色的边 的边权之和。
k <= 2 的解法
(对偶最短路) O(n)
对于 k<2,只有一个附加点,故连通块颜色相同,则答案为 0
对于 k=2 若两附加点颜色一致,连通块颜色相同,则答案为 0.
否则,这个图上会有 一黑一白两连通块。
下图对应本题的样例(借一张图)
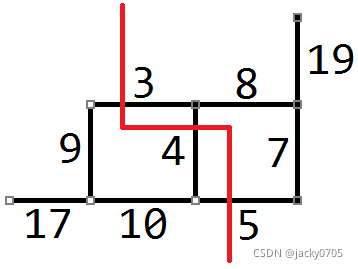
红线经过的边权为 3+4+5=12。
现在,我们的问题转化成了:在这张图上找一条线,使得这条线把这张图分为两块,并且 线上的边权之和 最小
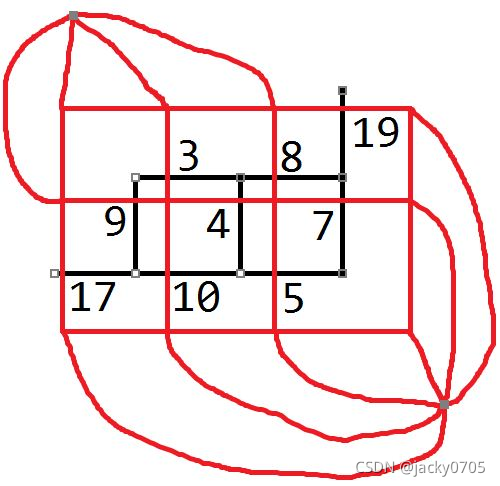
这是一张 偶图,即把 格子看作 点,然后把 格子之间隔着的边 变为 连接两个格子的点的边
由图可见,起点 和 终点 分别位于两个 附加点 连成的长方形的 两侧,
这是因为一条 分割线 一定经过 两个附加点的不同侧,否则无法把它们两个分开,所以两个点必须在不同侧。
最后,用 Dijkstra 算法求 起点 到 终点 的最短路即可
期望得分:45 分
算法二
(对偶最短路 + 区间 Dp) O(∑(ki)⋅mnlog(mn)+∑(k3i))
以下内容有亿点点复杂,水平不足者请就此打住,您已经拥有 345 的高分了。
迈出勇敢的一步 k = 3
让我们改一下样例(没错,又是蹭图
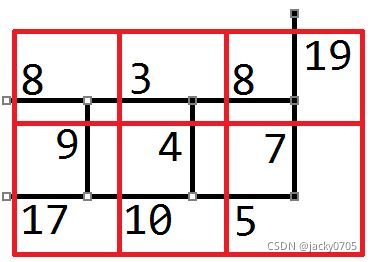
可见,在 (1,1) 位置的点 往左延伸 出一个附加点。
因为点被染上的颜色只有 黑白两种,所以必然可以找到两个同色点,
那么我们可以把这两个点当成 同一个点 进行处理:
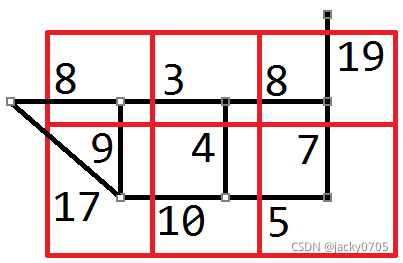
这样,我们就知道了 起点 和 终点 的位置!
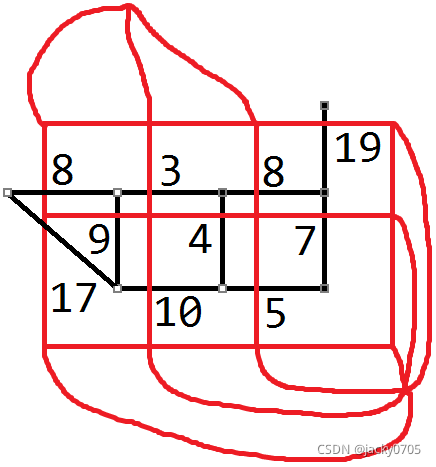
虚线连接的是除了 起点和终点 以外的所有 同侧边上的点。
问题解决。
问题扩展 k > 2
通过上面的 k=3 的情况,我们发现我们可以将所有 相邻的同色附加点 合并,将它们 看为一个点
如果有好多点,又该如何处理呢?
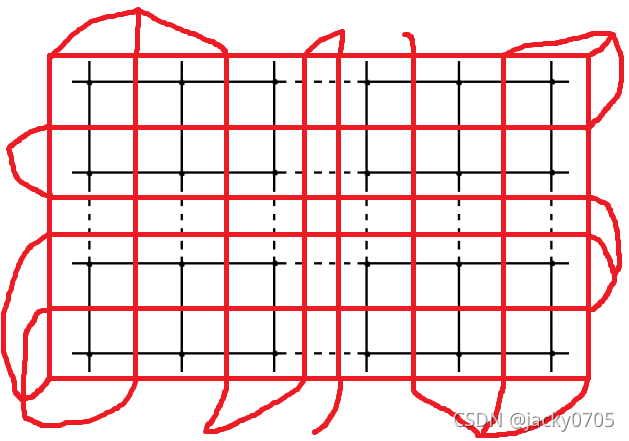
上图中,黑色的是原图,红色的是我们转化后的 对偶图。
我们现在要做的,就是把图上的 异色 附加点 两两配对 为 起点和终点,让所有点都有自己的 伴点。
最后,将 可以两两配对的异色点 的 最短路径上的 所有边的权值之和相加即可。
那么,我们该如何配对这些点呢?
如果是直接直接枚举 所有配对方案,那么时间复杂度会飙升到 O(k!),无法接受!
我们需要找到一些性质,来降低枚举的方案数量,也就是 可行性剪枝。
思考一下,异色的附加点 两两配对 后 最短距离和最小 需要满足什么样的性质?
有 A,B,C,D 四个可配对的点,顺时针摆放后 若按 (A,C)、(B,D) 顺序配对,会造成如下情况:
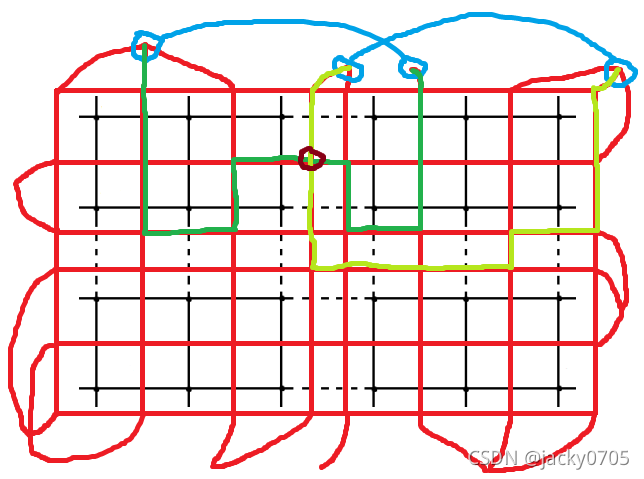
因为它们是交叉着配对的,其最短路必定在一个位置相交,棕色的点就是其相交处。
如此,我们会惊讶的发现,要是将 (1,2)、(3,4) 进行配对呢?
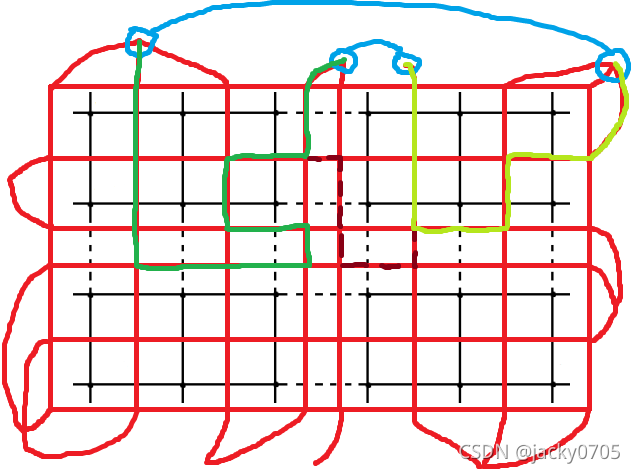
如图可见,最终答案显然要优于上一种。
由此,我们总结出了一个规律:配对的点 组成的最短路 不能交叉!
哎,这个规律好熟悉呀,不就是括号序列嘛!
举个例子:若 A 为合法的括号序列,则 AA、(A) 都合法。
那我们要枚举的 配对方案 和 括号序列的方案 一一对应。
于是,我们求出求出 任意两个 起点、终点之间的最短路。
最后用区间 Dp 求出 配对方案中 最小权值之和。
因为这个序列构成一个环形,所以,我们需要 断链加一倍 来实现。
至此,我们实现了所有的操作:
一、 建出 转化后的图
二、 求出 任意两个 起点、终点之间的最短路
三、 用 括号序列 的区间 DP 操作求出 最小值


# Orz
大神,第四题没有代码?
TQL!!!!大神贴贴
good