(1)求组合数 I
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cabmod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 2010;
const int mod = 1e9 + 7;
int c[N][N];
void init() //预处理出所有的组合数 N比较小
{
for(int i=0;i<N;i++)
{
for(int j=0;j<=i;j++)
{
if(!j)c[i][j]=1;
else
{
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
}
}
}
}
int main()
{
int n;
scanf("%d",&n);
init();
while(n--)
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",c[a][b]);
}
return 0;
}
数三角形
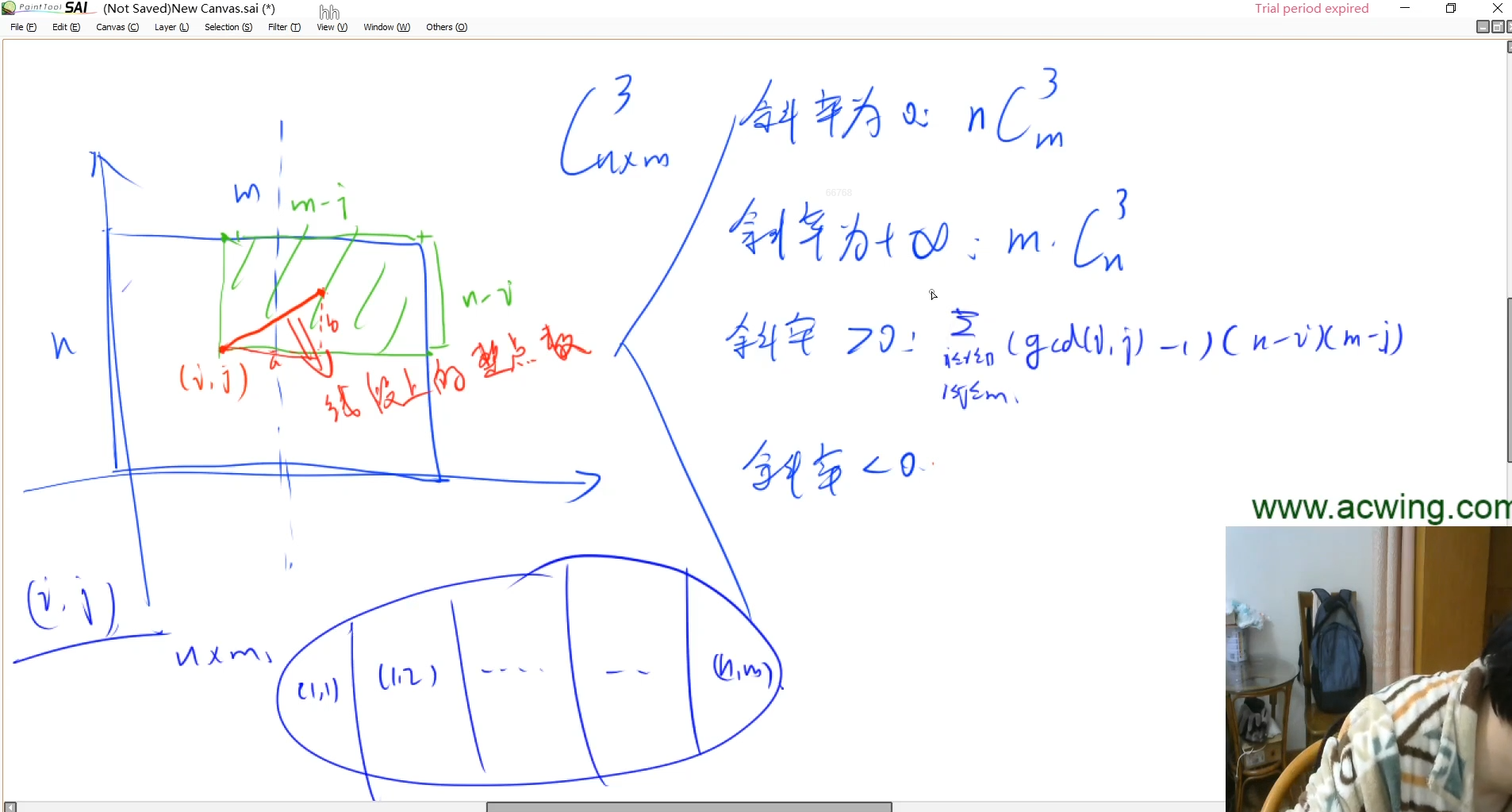
给定一个 n×m 的网格,请计算三点都在格点上的三角形共有多少个。
下图为 4×4 的网格上的一个三角形。
a.png
注意:三角形的三点不能共线。
输入格式
输入一行,包含两个空格分隔的正整数 m 和 n。
输出格式
输出一个正整数,为所求三角形数量。
数据范围
1≤m,n≤1000
输入样例:
2 2
输出样例:
76
代码:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
LL C(int n)
{
return (LL)n*(n-1)*(n-2)/6;
}
int main()
{
int n, m;
cin >> n >> m;
n ++, m ++ ;
LL res = C(n * m) - (LL)n * C(m) - (LL)m * C(n);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
res -= 2ll * (gcd(i, j) - 1) * (n - i) * (m - j);
cout << res << endl;
return 0;
}
(2)求组合数 II
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N =1e6+10;
const int mod = 1e9+7;
typedef long long LL;
int fact[N];
int infact[N];
int q_mi(int a,int k,int mod)
{
int res=1;
while(k)
{
if(k&1)
{
res=(LL)res*a%mod;
}
a=(LL)a*a%mod;
k>>=1;
}
return res;
}
int main()
{
int n;
fact[0]=1;
infact[0]=1;
for(int i=1;i<N;i++)
{
fact[i]=i*(LL)fact[i-1]%mod;
infact[i] = (LL)infact[i-1]*q_mi(i,mod-2,mod)%mod;
}
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
}
车的放置
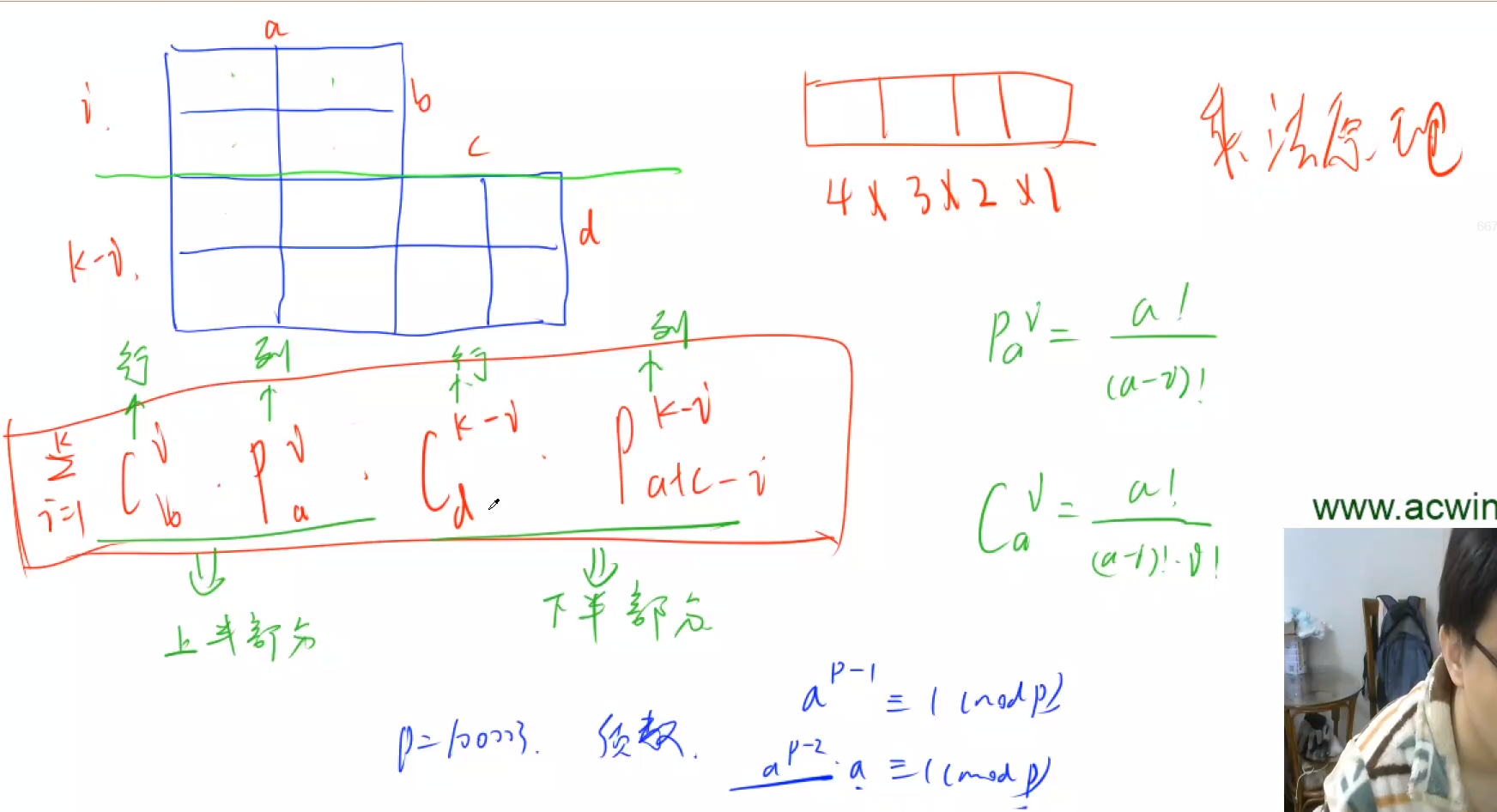
有下面这样的一个网格棋盘,a,b,c,d 表示了对应边长度,也就是对应格子数。
1.png
当 a=b=c=d=2 时,对应下面这样一个棋盘:
2.png
要在这个棋盘上放 k 个相互不攻击的车,也就是这 k 个车没有两个车在同一行,也没有两个车在同一列,问有多少种方案。
只需要输出答案 mod100003 后的结果。
输入格式
共一行,五个非负整数 a,b,c,d,k。
输出格式
包括一个正整数,为答案 mod100003 后的结果。
数据范围
0≤a,b,c,d,k≤1000,
保证至少有一种可行方案。
输入样例:
2 2 2 2 2
输出样例:
38
代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2010, mod = 100003; //100003是个质数
int fact[N], infact[N];
int qmi(int a, int k)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % mod;
a = (LL)a * a % mod;
k >>= 1;
}
return res;
}
int C(int a, int b)
{
if (a < b) return 0;
return (LL)fact[a] * infact[a - b] % mod * infact[b] % mod;
}
int P(int a, int b)
{
if (a < b) return 0;
return (LL)fact[a] * infact[a - b] % mod;
}
int main()
{
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2) % mod;
}
int a, b, c, d, k;
cin >> a >> b >> c >> d >> k;
int res = 0;
for (int i = 0; i <= k; i ++ )
{
res = (res + (LL)C(b, i) * P(a, i) % mod * C(d, k - i) % mod * P(a + c - i, k - i)) % mod;
}
cout << res << endl;
return 0;
}
(3)求组合数 III
给定 n 组询问,每组询问给定三个整数 a,b,p,其中 p 是质数,请你输出 Cbamodp 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a,b,p。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
代码:
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if(a<p&&b<p)return C(a,b,p);
return (LL)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
序列统计
给定三个正整数 N,L,R,统计长度在 1 到 N 之间,元素大小都在 L 到 R 之间的单调不降序列的数量。
输出答案对 106+3 取模的结果。
输入格式
输入第一行包含一个整数 T,表示数据组数。
第二到第 T+1 行每行包含三个整数 N,L,R。
输出格式
输出包含 T 行,每行有一个数字,表示你所求出的答案对 106+3 取模的结果。
数据范围
1≤N,L,R≤109,
1≤T≤100,
输入数据保证 L≤R。
输入样例:
2
1 4 5
2 4 5
输出样例:
2
5
样例解释
对于第一组输入,满足条件的两个序列为 {4},{5}。
代码:

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int p = 1000003;
int qmi(int a, int k)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b)
{
if (a < b) return 0;
int down = 1, up = 1;
for (int i = a, j = 1; j <= b; i --, j ++ )
{
up = (LL)up * i % p;
down = (LL)down * j % p;
}
return (LL)up * qmi(down, p - 2) % p;
}
int Lucas(int a, int b)
{
if (a < p && b < p) return C(a, b);
return (LL)Lucas(a / p, b / p) * C(a % p, b % p) % p;
}
int main()
{
int T;
cin >> T;
while (T -- )
{
int n, l, r;
cin >> n >> l >> r;
cout << (Lucas(r - l + n + 1, r - l + 1) + p - 1) % p << endl;
}
return 0;
}
(4)求组合数IV
输入 a,b,求 Cba 的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数 a 和 b。
输出格式
共一行,输出 Cba 的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
代码
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)
{
break;
}
}
}
}
int get(int n, int p)
{
int res=0;
while(n)
{
res=res+n/p;
n=n/p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t=0;
for(int i=0;i<a.size();i++)
{
t=t+a[i]*b;
c.push_back(t%10);
t=t/10;
}
while(t)
{
c.push_back(t%10);
t=t/10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
puts("");
return 0;
}
(5)有趣的数列
我们称一个长度为 2n 的数列是有趣的,当且仅当该数列满足以下三个条件:
它是从 1 到 2n 共 2n 个整数的一个排列 {ai};
所有的奇数项满足 a1<a3<⋯<a2n−1 ,所有的偶数项满足 a2<a4<⋯<a2n;
任意相邻的两项 a2i−1 与 a2i (1≤i≤n) 满足奇数项小于偶数项,即:a2i−1<a2i。
任务是:对于给定的 n,请求出有多少个不同的长度为 2n 的有趣的数列。
因为最后的答案可能很大,所以只要求输出答案 modP 的值。
输入格式
只包含用空格隔开的两个整数 n 和 P。
输出格式
仅含一个整数,表示不同的长度为 2n 的有趣的数列个数 modP 的值。
数据范围
1≤n≤106,
2≤P≤109
输入样例:
3 10
输出样例:
5
样例解释
对应的 5 个有趣的数列分别为 {1,2,3,4,5,6},{1,2,3,5,4,6},{1,3,2,4,5,6},{1,3,2,5,4,6},{1,4,2,5,3,6}。
代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int N = 2e6+10; //计算卡特兰数 用到C2n
bool st[N];
int cnt;
int primes[N];
int n;
int p;
void init(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] * i <= n; j ++ )
{
st[i * primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n,int p)
{
int res=0;
while(n)
{
res+=n/p;
n/=p;
}
return res;
}
int qmi(int a,int b)
{
int res=1;
while(b)
{
if(b&1)res=res*a%p;
b>>=1;
a=(ll)a*a%p;
}
return res;
}
int C(int a,int b)
{
int res=1;
for(int i=0;i<cnt;i++)
{
int prime=primes[i];
int s=get(a,prime)-get(a-b,prime)-get(b,prime);
res = (ll)res * qmi(prime, s) % p;
}
return res;
}
int main()
{
cin>>n>>p;
init(2*n);
//计算卡特兰数的公式
cout << (C(n * 2, n) - C(n * 2, n - 1) + p) % p << endl;
return 0;
}
(6)牡牛和牝牛
约翰要带 N 只牛去参加集会里的展示活动,这些牛可以是牡牛,也可以是牝牛。
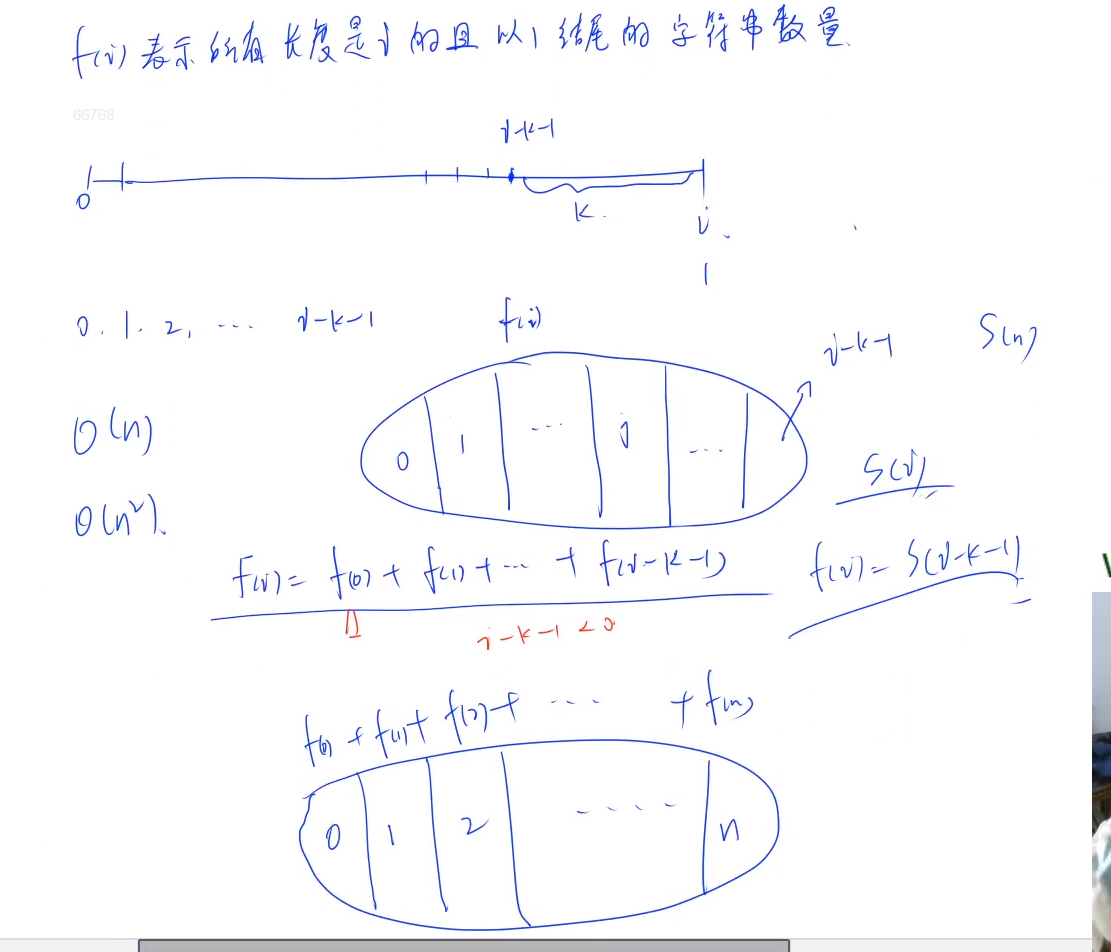
牛们要站成一排,但是牡牛是好斗的,为了避免牡牛闹出乱子,约翰决定任意两只牡牛之间至少要有 K 只牝牛。
请计算一共有多少种排队的方法,所有牡牛可以看成是相同的,所有牝牛也一样,答案对 5000011 取模。
输入格式
一行,输入两个整数 N 和 K。
输出格式
一个整数,表示排队的方法数。
数据范围
1≤N≤105,
0≤K<N
输入样例:
4 2
输出样例:
6
样例解释
6 种方法分别是:牝牝牝牝,牡牝牝牝,牝牡牝牝,牝牝牡牝,牝牝牝牡,牡牝牝牡。
代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1e5+10,mod=5000011;
int a[N];
int s[N];
int main()
{
int n;
int k;
cin>>n>>k;
s[0]=1;
a[0]=1;
for(int i=1;i<=n;i++)
{
a[i]=s[max(0,i-k-1)];
s[i]=(s[i-1]+a[i])%mod;
}
cout<<s[n];
return 0;
}
(6)方程的解
佳佳碰到了一个难题,请你来帮忙解决。
对于不定方程 a1+a2+⋯+ak−1+ak=g(x),其中 k≥1 且 k∈N∗,x 是正整数,g(x)=xxmod1000(即 xx 除以 1000 的余数),x,k 是给定的数。
我们要求的是这个不定方程的正整数解组数。
举例来说,当 k=3,x=2 时,方程的解分别为:
⎧⎩⎨a1=1a2=1a3=2 ⎧⎩⎨a1=1a2=2a3=1 ⎧⎩⎨a1=2a2=1a3=1
输入格式
有且只有一行,为用空格隔开的两个正整数,依次为 k,x。
输出格式
有且只有一行,为方程的正整数解组数。
数据范围
1≤k≤100,
1≤x<231,
k≤g(x)
输入样例:
3 2
输出样例:
3
难度:中等
时/空限制:1s / 128MB
总通过数:1008
总尝试数:1986
来源:《信息学奥赛一本通》
算法标签

代码:
#include <iostream>
using namespace std;
typedef long long LL;
// 1000的阶乘除以100的阶乘除以900的阶乘 为10的一百四十多位
// 开N = 150足够
const int N =150;
int f[1000][100][N];//f[i][j]表示求Cij
int k , x;
int qmi(int a, int b, int mod)
{
int res = 1;
while(b)
{
if(b & 1) res = (LL) res * a % mod;
b >>= 1;
a = (LL) a * a % mod;
}
return res;
}
void add(int c[] , int a[] , int b[])
{
for(int i = 0 , t = 0 ; i < N ; i++)
{
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
}
int main()
{
cin >> k >> x;
int n = qmi(x % 1000 , x , 1000);
//C(n-1 , k-1),因为题目中没有说取模,所以要用到高精度
for(int i = 0 ; i < n ; i++)
for(int j = 0 ; j <= i && j < k ; j++)//C右上角<=C右下角,C右上角 <= k-1
if(!j) f[i][j][0] = 1;
else add(f[i][j] , f[i - 1][j] , f[i - 1][j - 1]);
int *g = f[n - 1][k - 1];// 把f[i][j][]看成a[]
int k = N - 1;
while(!g[k]) k--; //先去掉前导零,再输出g
while(k >= 0) cout << g[k--];
return 0;
}

