(1)欧拉函数
给定 n 个正整数 ai,请你求出每个数的欧拉函数。
欧拉函数的定义
1∼N 中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)。
若在算数基本定理中,N=p1的a1次方p2的a2次方…pamm,则:
ϕ(N) = N×p1−1/p1×p2−1/p2×…×pm−1/pm
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
输出共 n 行,每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例:
3
3
6
8
输出样例:
2
2
4
代码
#include<iostream>
using namespace std;
int phi(int x)
{
int res=x;
for(int i=2;i<=x/i;i++)
{
if(x%i==0)
{
res=res/i*(i-1);
while(x%i==0)
{
x=x/i;
}
}
}
if (x > 1) res = res / x * (x - 1);
return res;
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int k;
scanf("%d",&k);
printf("%d\n",phi(k));
}
return 0;
}
(2)筛法求欧拉函数
给定一个正整数 n,求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示 1∼n 中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例:
6
输出样例:
12
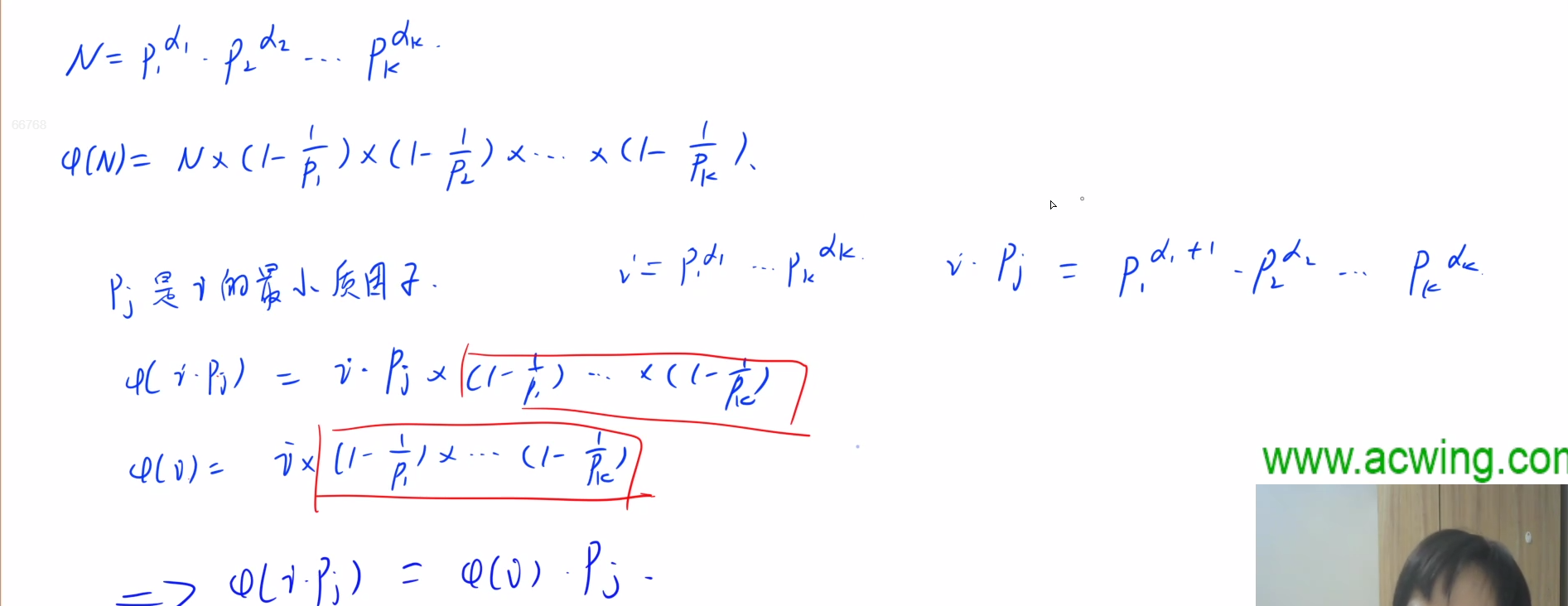
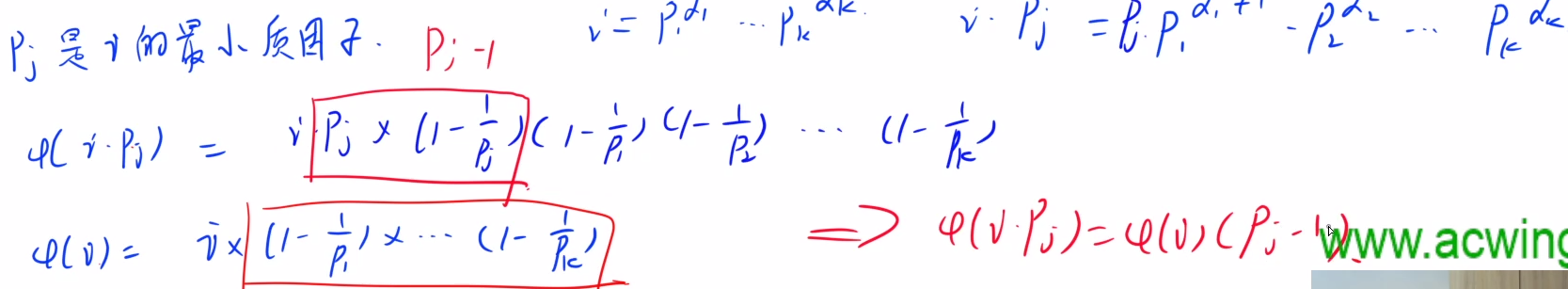
代码:
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int primes[N], cnt; //primes数组存所有的质因子,cnt是下标
int phi[N]; //欧拉函数
bool st[N]; //表示每个数是否被筛掉了
LL get_eulers(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; i ++) //线性筛
{
if (!st[i]) //当前没有被筛过就是质数
{
primes[cnt ++] = i;
phi[i] = i - 1; //质数的欧拉函数
}
for (int j = 0; primes[j] <= n / i; j ++)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)
{
phi[primes[j] * i] = phi[i] * primes[j];
break;
}
phi[primes[j] * i] = phi[i] * (primes[j] - 1);
}
}
LL res = 0;
for (int i = 1; i <= n; i ++)
res += phi[i];
return res;
}
int main()
{
int n;
cin >> n;
cout << get_eulers(n) << endl;
return 0;
}
(3)可见的点
在一个平面直角坐标系的第一象限内,如果一个点 (x,y) 与原点 (0,0) 的连线中没有通过其他任何点,则称该点在原点处是可见的。
例如,点 (4,2) 就是不可见的,因为它与原点的连线会通过点 (2,1)。
部分可见点与原点的连线如下图所示:
3090_1.png
编写一个程序,计算给定整数 N 的情况下,满足 0≤x,y≤N 的可见点 (x,y) 的数量(可见点不包括原点)。
输入格式
第一行包含整数 C,表示共有 C 组测试数据。
每组测试数据占一行,包含一个整数 N。
输出格式
每组测试数据的输出占据一行。
应包括:测试数据的编号(从 1 开始),该组测试数据对应的 N 以及可见点的数量。
同行数据之间用空格隔开。
数据范围
1≤N,C≤1000
输入样例:
4
2
4
5
231
输出样例:
1 2 5
2 4 13
3 5 21
4 231 32549

代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
bool st[N];
int cnt;
int phi[N];
int primes[N];
int n;
void init(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(!st[i])
{
primes[cnt++]=i;
phi[i]=i-1;
}
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)
{
phi[primes[j]*i]=phi[i]*primes[j];
break;
}
phi[primes[j]*i]=phi[i]*(primes[j]-1);
}
}
}
int main()
{
init(N - 1);
int n, m;
cin >> m;
for (int T = 1; T <= m; T ++ )
{
cin >> n;
int res = 1;
for (int i = 1; i <= n; i ++ ) res += phi[i] * 2;
cout << T << ' ' << n << ' ' << res << endl;
}
return 0;
}
(4)最大公约数
给定整数 N,求 1≤x,y≤N 且 GCD(x,y) 为素数的数对 (x,y) 有多少对。
GCD(x,y) 即求 x,y 的最大公约数。
输入格式
输入一个整数 N。
输出格式
输出一个整数,表示满足条件的数对数量。
数据范围
1≤N≤107
输入样例:
4
输出样例:
4


代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e7 + 10;
int primes[N], cnt;
bool st[N];
int phi[N];
LL s[N];
void init(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] * i <= n; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)
{
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
phi[i * primes[j]] = phi[i] * (primes[j] - 1);
}
}
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + phi[i];
}
int main()
{
int n;
cin >> n;
init(n);
LL res = 0;
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
res += s[n / p] * 2 + 1;
}
cout << res << endl;
return 0;
}
总结:统计有多少x,y,属于1到N中,x与y互质
(5)龙哥的问题
龙哥现在有一道题,要考考大家。
给定一个整数 N,请你求出 ∑1≤i≤N gcd(i,N)的值。
输入格式
一个整数 N。
输出格式
一个整数表示结果。
数据范围
1<N<231
输入样例:
6
输出样例:
15

代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 233, N = 1e5;
int primes[maxn], phi[maxn], cnt;
bool st[maxn];
void get_primes(int n)
{
phi[1] = 1;
for(int i = 2; i <= n; i++)
{
if(!st[i])
{
primes[cnt++] = i;
phi[i] = i - 1;
}
for(int j = 0; j < cnt && i * primes[j] <= n; j++)
{
st[i * primes[j]] = 1;
if(i % primes[j] == 0)
{
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
else phi[i * primes[j]] = phi[i] * (primes[j] - 1);
}
}
}
int euler(int n)
{
int ans = n;
for(int i = 0; i < cnt; i++)
{
//if(primes[i] * primes[i] > n) break;
if(n % primes[i] == 0)
{
ans = ans / primes[i] * (primes[i] - 1);
while(n % primes[i] == 0) n /= primes[i];
}
}
if(n > 1) ans = ans / n * (n - 1);
return ans;
}
int main()
{
get_primes(N);
ll n;
ll ans = 0;
cin >> n;
for(int i = 1; (ll)i * i <= n; i++)
{
if(n % i == 0)
{
int t = n / i;
if(t < N) ans += i * phi[t];
else ans += i * euler(t);
if(i != t)
{
ans += t * phi[i];
}
}
}
cout<<ans;
}
(6)最大公约数
给定两个正整数 a,m,其中 a<m。
请你计算,有多少个小于 m 的非负整数 x 满足:
gcd(a,m)=gcd(a+x,m)
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据占一行,包含两个整数 a,m。
输出格式
每组数据输出一行结果,一个整数,表示满足条件的非负整数 x 的个数。
数据范围
前三个测试点满足,1≤T≤10。
所有测试点满足,1≤T≤50,1≤a<m≤1010。
输入样例:
3
4 9
5 10
42 9999999967
输出样例:
6
1
9999999966
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL T;
LL _gcd(LL a, LL b)
{
return b?_gcd(b, a % b):a;
}
LL phi(LL n)
{
LL res = n;
for (int i = 2; i <= n / i; i ++ )
{
if (n % i == 0) res = res / i * (i - 1);
while (n % i == 0) n /= i;
}
if (n > 1) res = res / n * (n - 1);
return res;
}
int main()
{
scanf("%lld", &T);
while (T -- )
{
LL a, m;
scanf("%lld %lld", &a, &m);
LL gcd = _gcd(a, m);
LL ans = phi(m / gcd);
printf("%lld\n", ans);
}
return 0;
}

