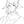图的定义：

图G由顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中顶点的有限非空集；E(G)表示图G中顶点之间的关系（边）合。若V= {v1,v2,… ,vn}，则用|V|表示图G中顶点的个数，也称图G的阶，E= {(u,v)|uÎV,vÎV}，用|E|表示图G中边的条数
注意：线性表可以是空表，树可以是空树，但图不可以是空，即V一定是非空集

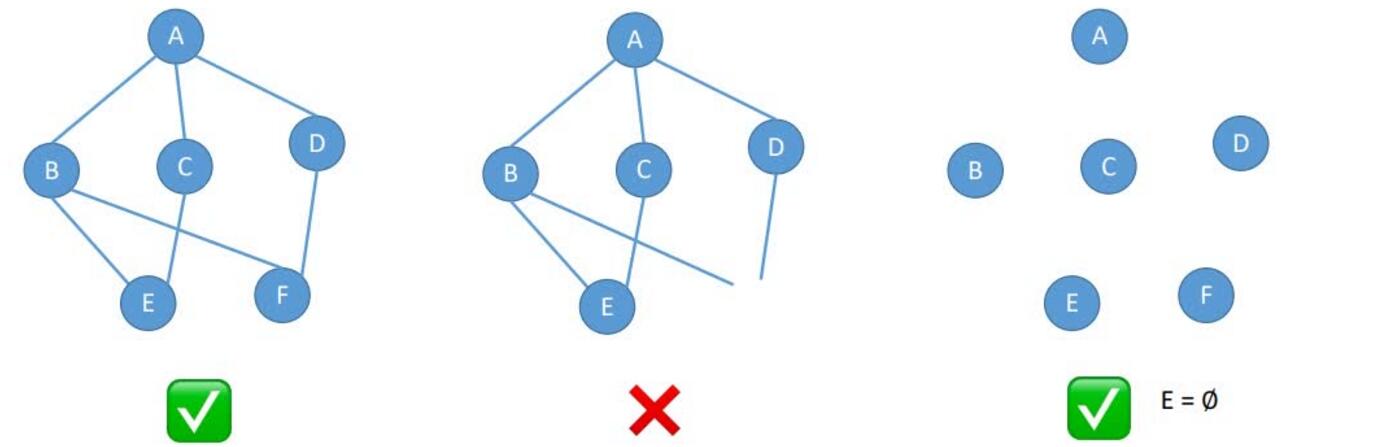
有向图：

无向图：

简单图： 1.不存在重复边； 2.不存在顶点到自身的边；

多重图： 图G中某两个结点之间的边数多于一条，又允许顶点通过同一条边和自己关联，则G为多重图

顶点的度、入度、出度：

有向图：

无向图：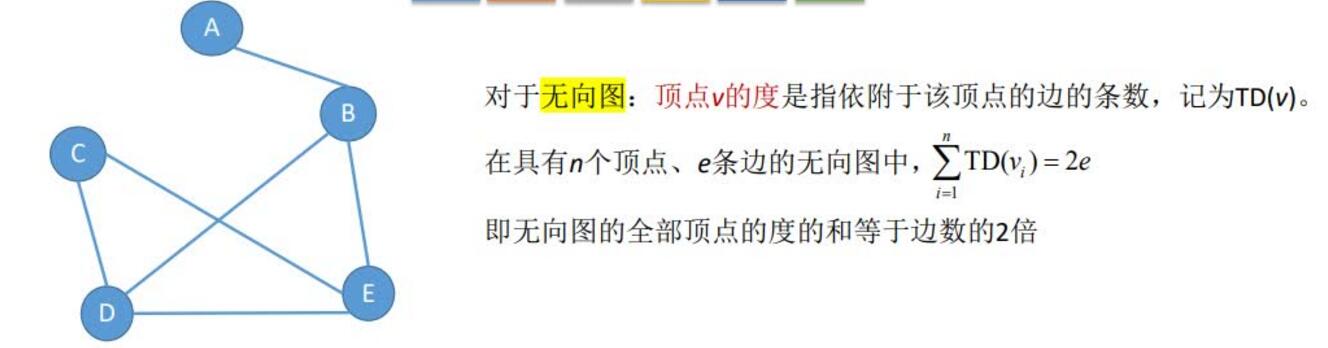

顶点-顶点的关系描述：

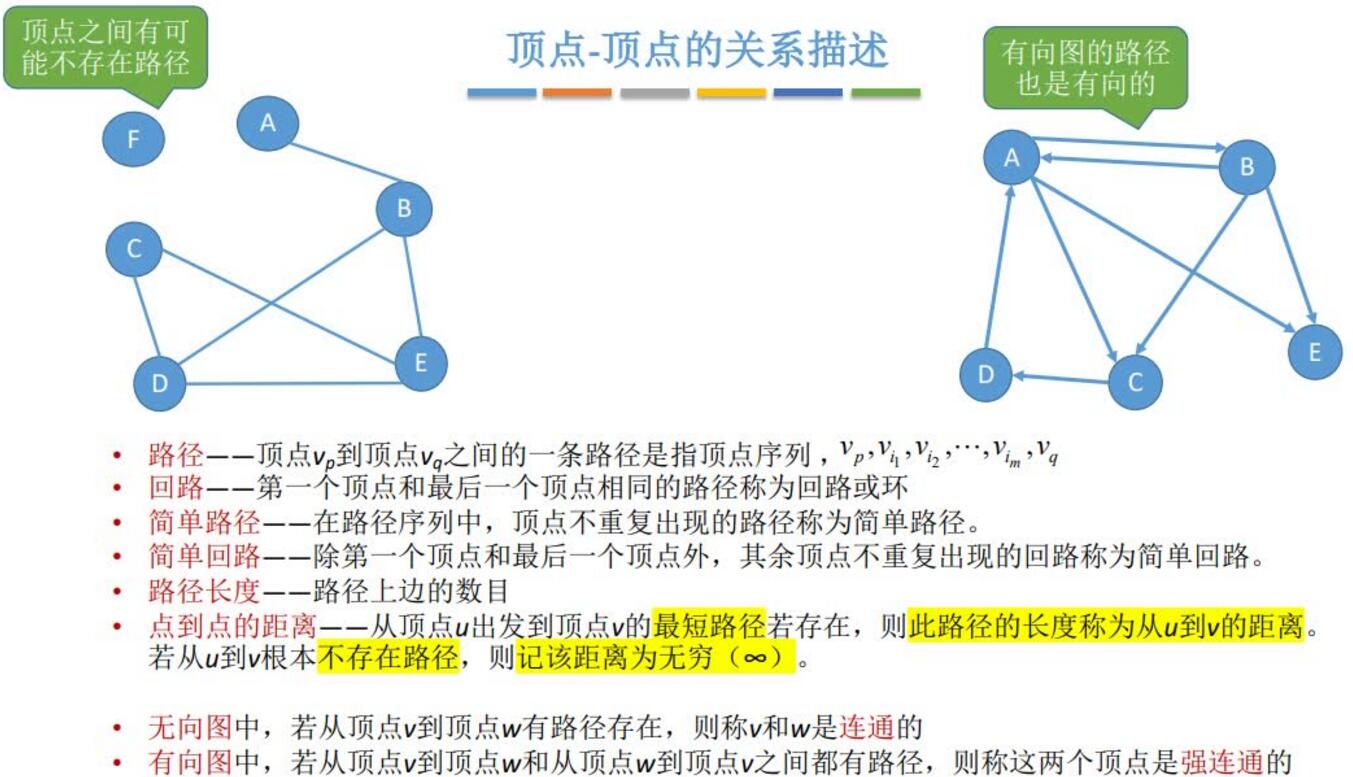
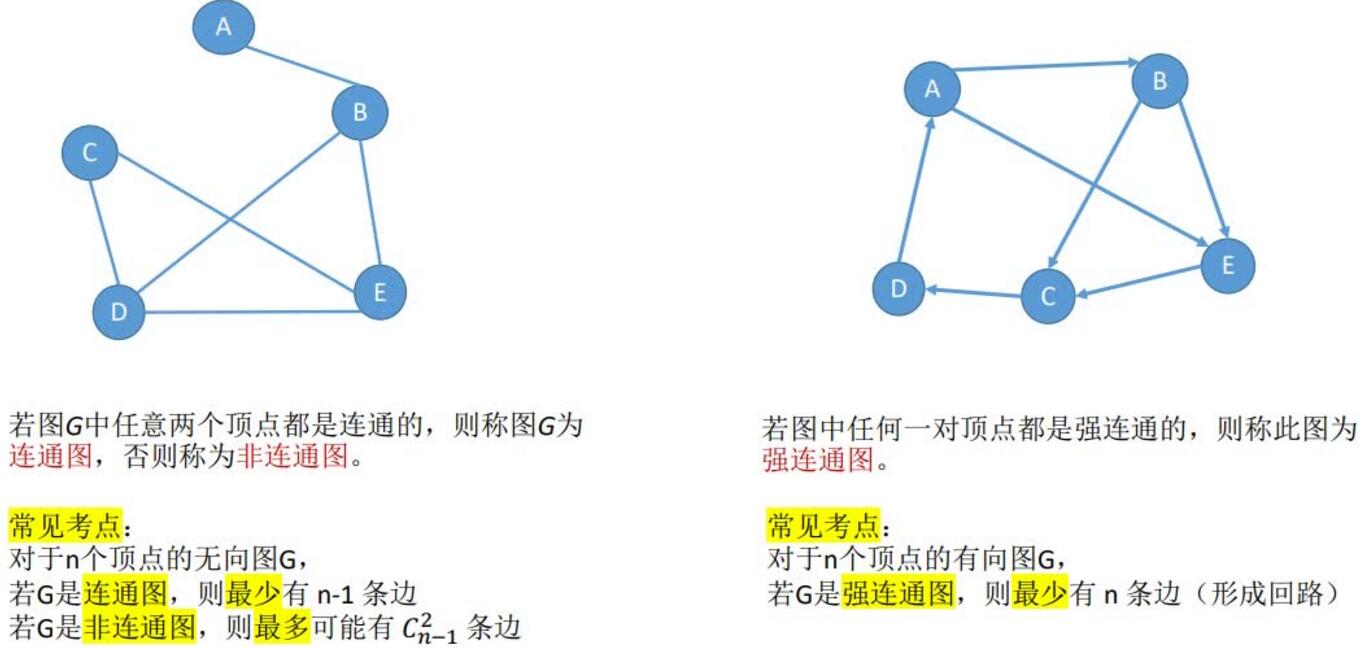
连通图：

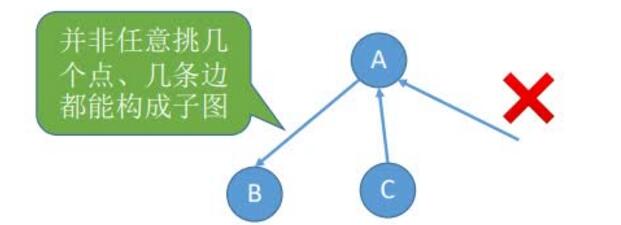
子图：
设有两个图G= (V,E)和G’= (V’,E’)，若V’是V的子集，且E’是E的子集，则称G’是G的子图
生成子图：若有满足V(G’) =V(G)的子图G’，则称其为G的生成子图

【连通分量】

最大连通子图：子图必须连通，且包含尽可能多的顶点和边

最大强连通子图：子图必须强连通，同时保留尽可能多的边

连通分量:无向图中的最大连通子图称为连通分量

强连通分量:无向图中的最大强连通子图称为强连通分量

生成树：连通图的生成树是包含图中全部顶点的一个极小连通子图
若图中顶点数为n，则它的生成树含有n-1条边
对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路

生成森林：在非连通图中，连通分量的生成树构成了非连通图的生成森林

边的权： 在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值

带权图/网： 边上带有权值的图称为带权图，也称网

带权路径长度： 当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

【特殊形态的图】

无向完全图： 无向图中任意两个顶点之间都存在边

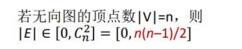
有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧

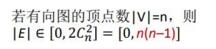
稀疏图： 边数很少的图称为稀疏图，反之称为稠密图（没有绝对的界限，一般来说|E|<|V|log|V|时，可以将G视为稀疏图）

树： 不存在回路，且连通的无向图
常见考点：n个顶点的图，若|E|>n-1，则一定有回路
n个顶点的树，必有n-1条边

有向树： 个顶点的入度为0、其余顶点的入度均为1的有向图，称为有向树。

总结：