二叉排序树：

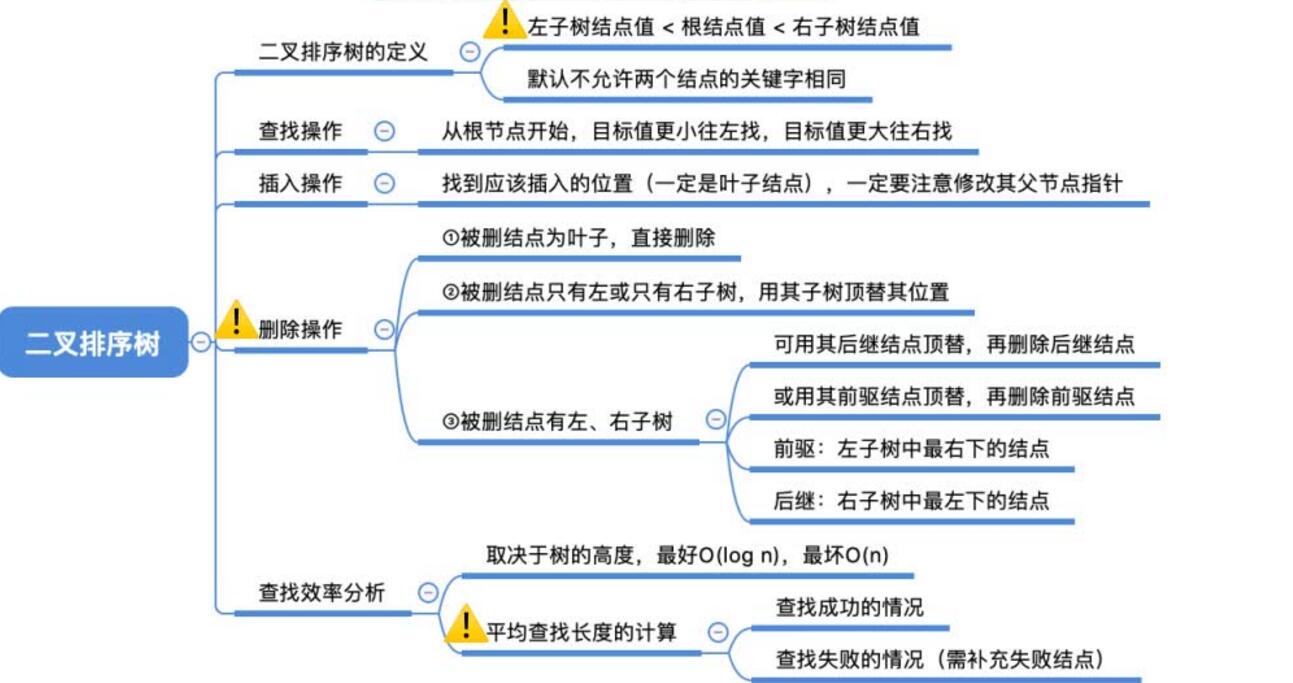
定义：

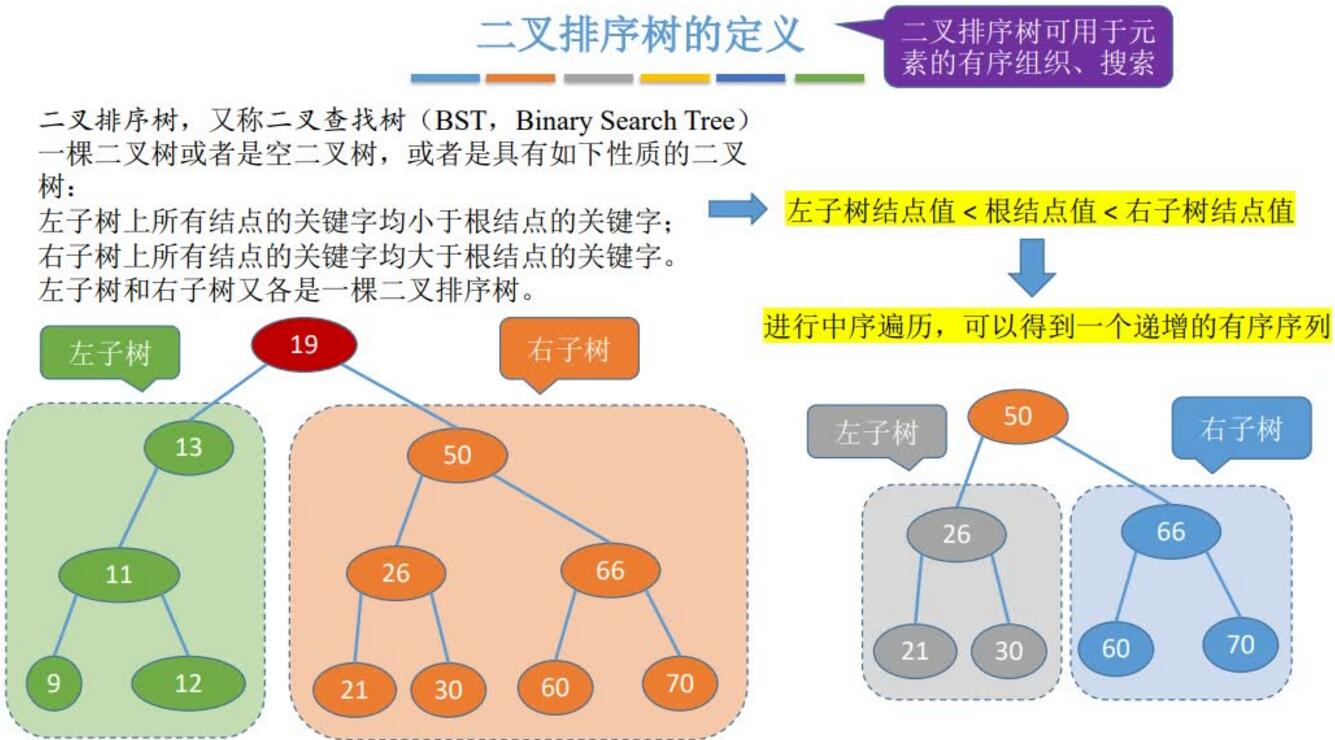
查找：

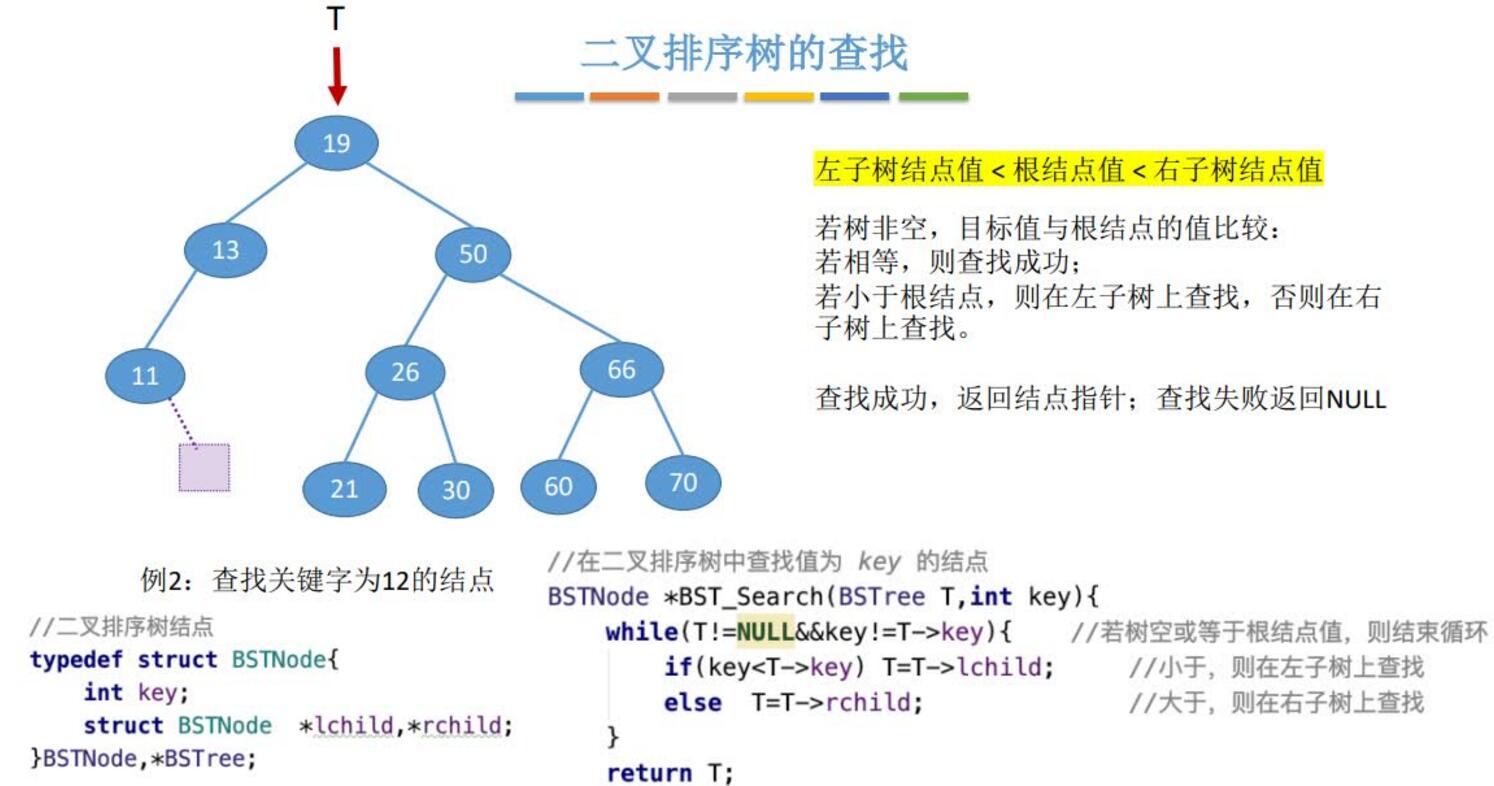
构造：

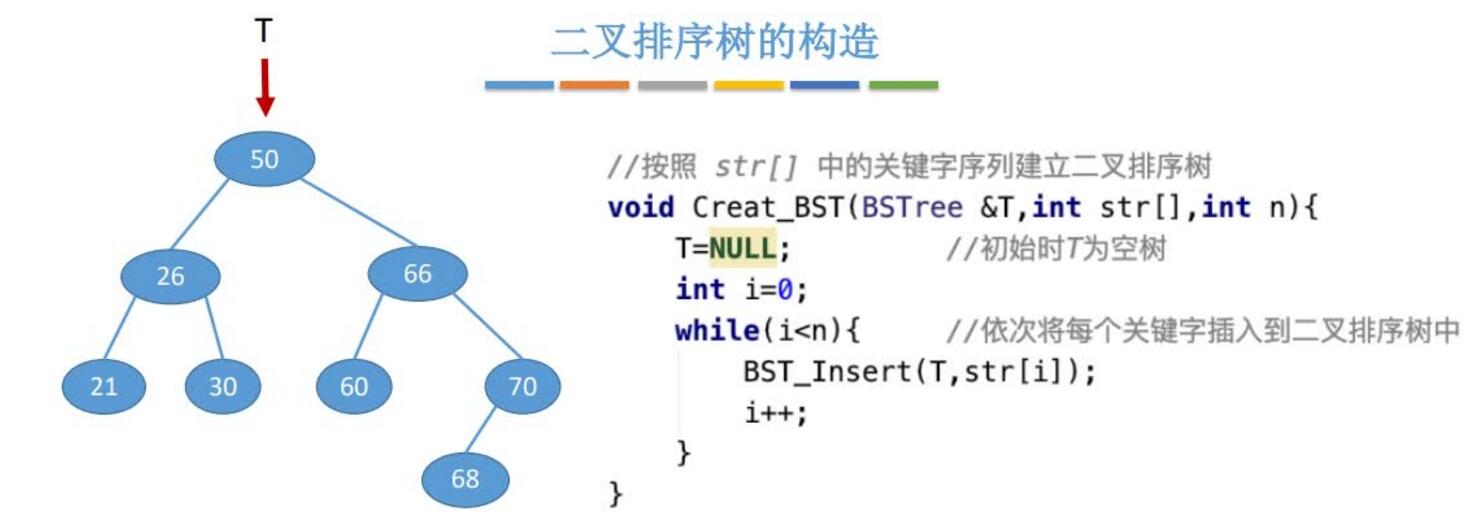
不同的关键字序列可能得到同款二叉排序树，也可能得到不同款二叉排序树

插入：

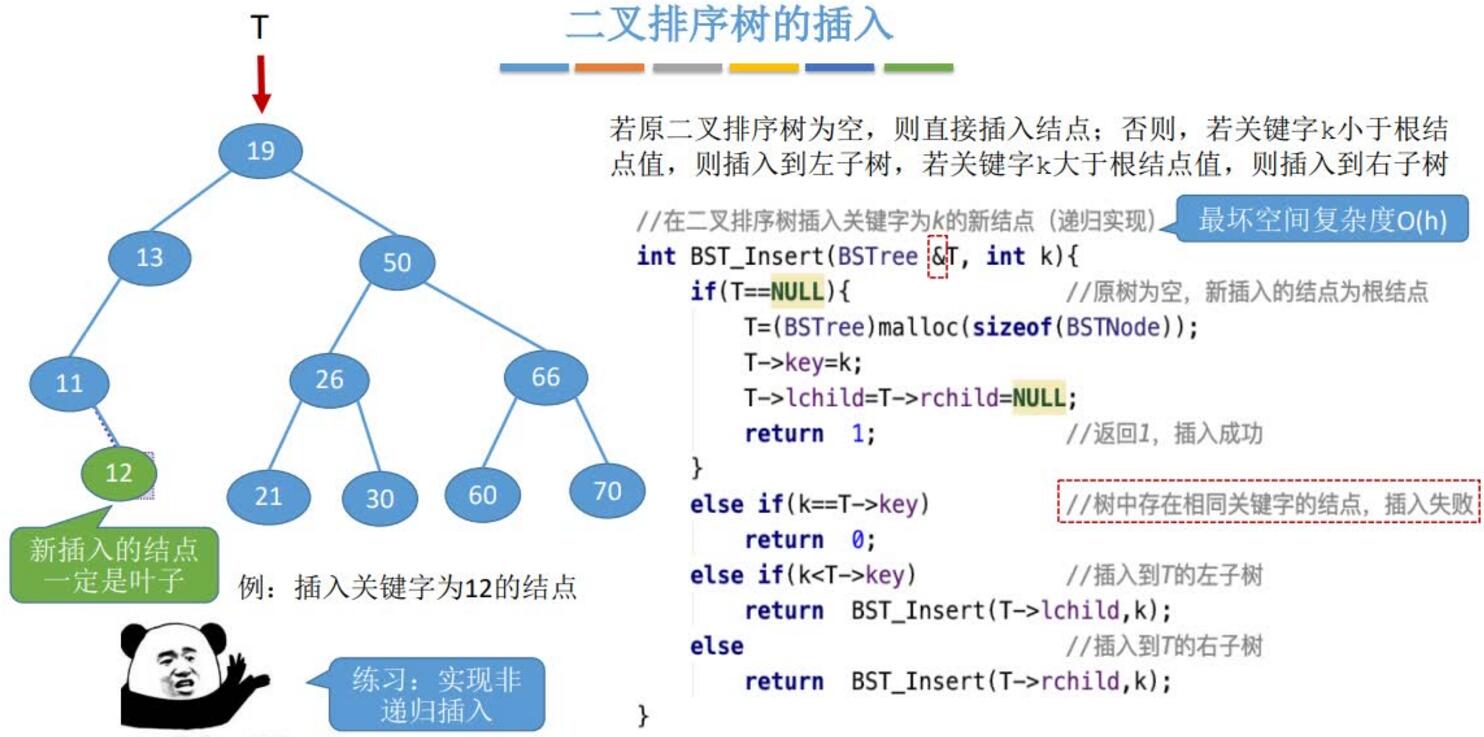
删除：

先搜索找到目标结点：若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质

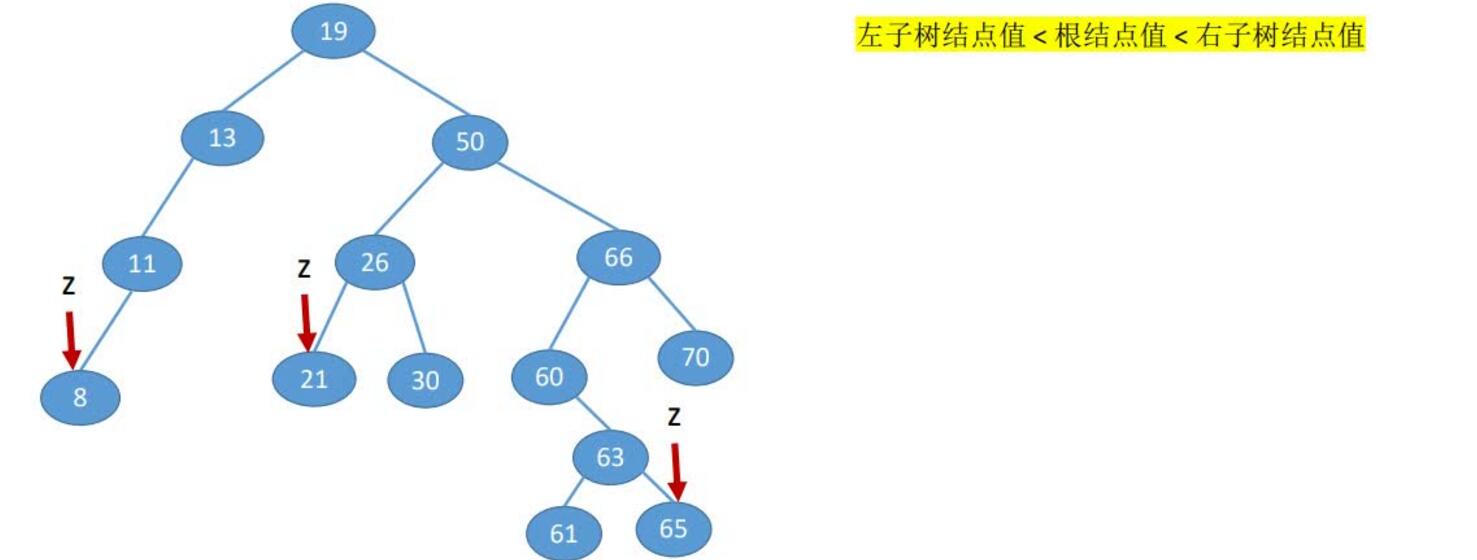
若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置

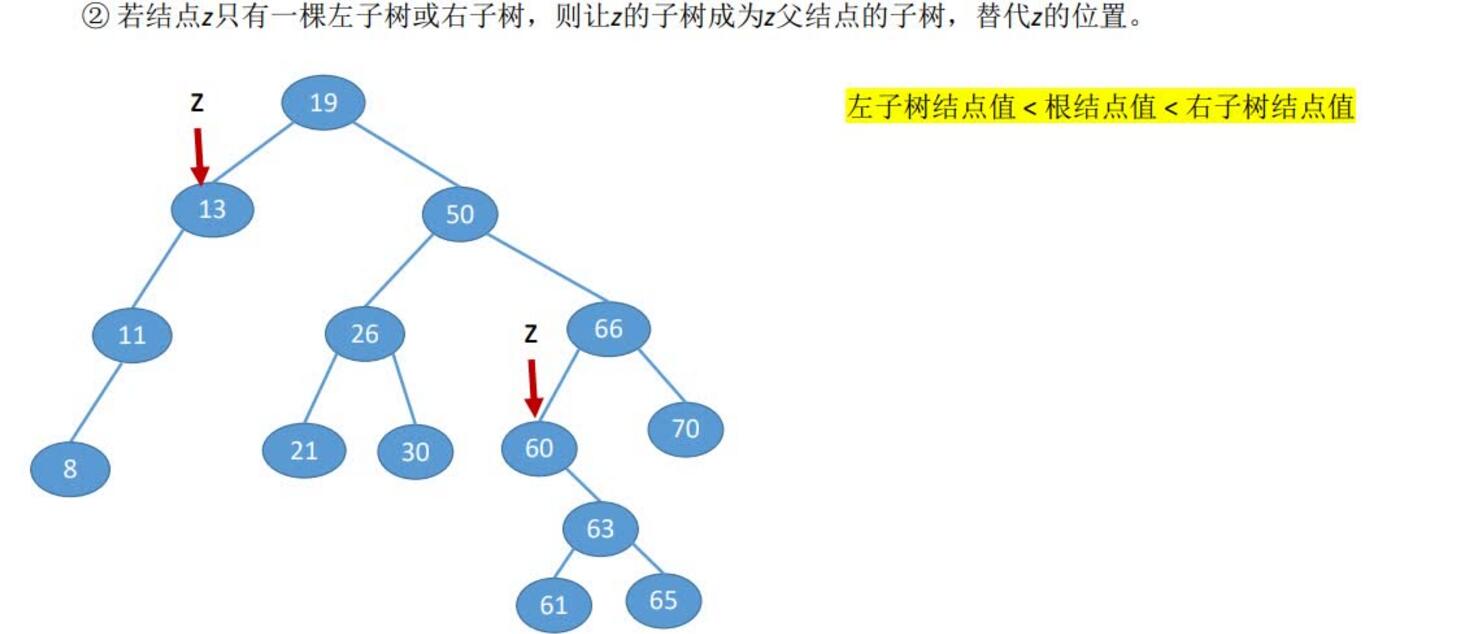
若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前），这样就转换成了第一或第二种情况。

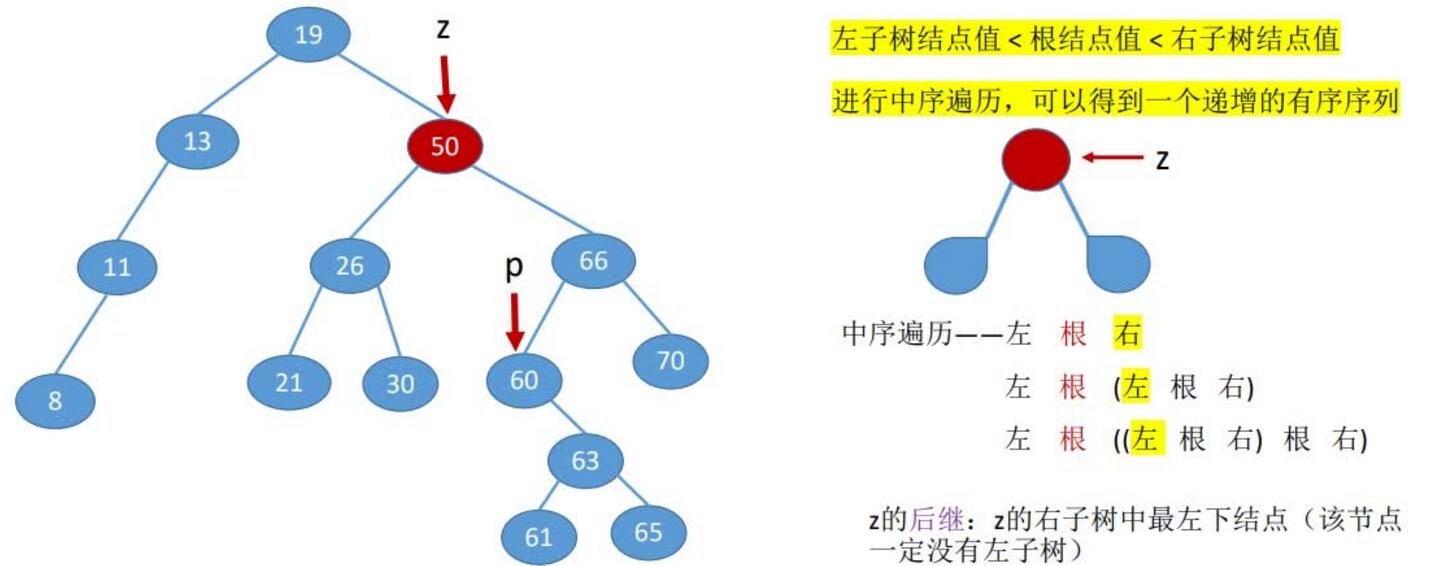
查找效率分析：

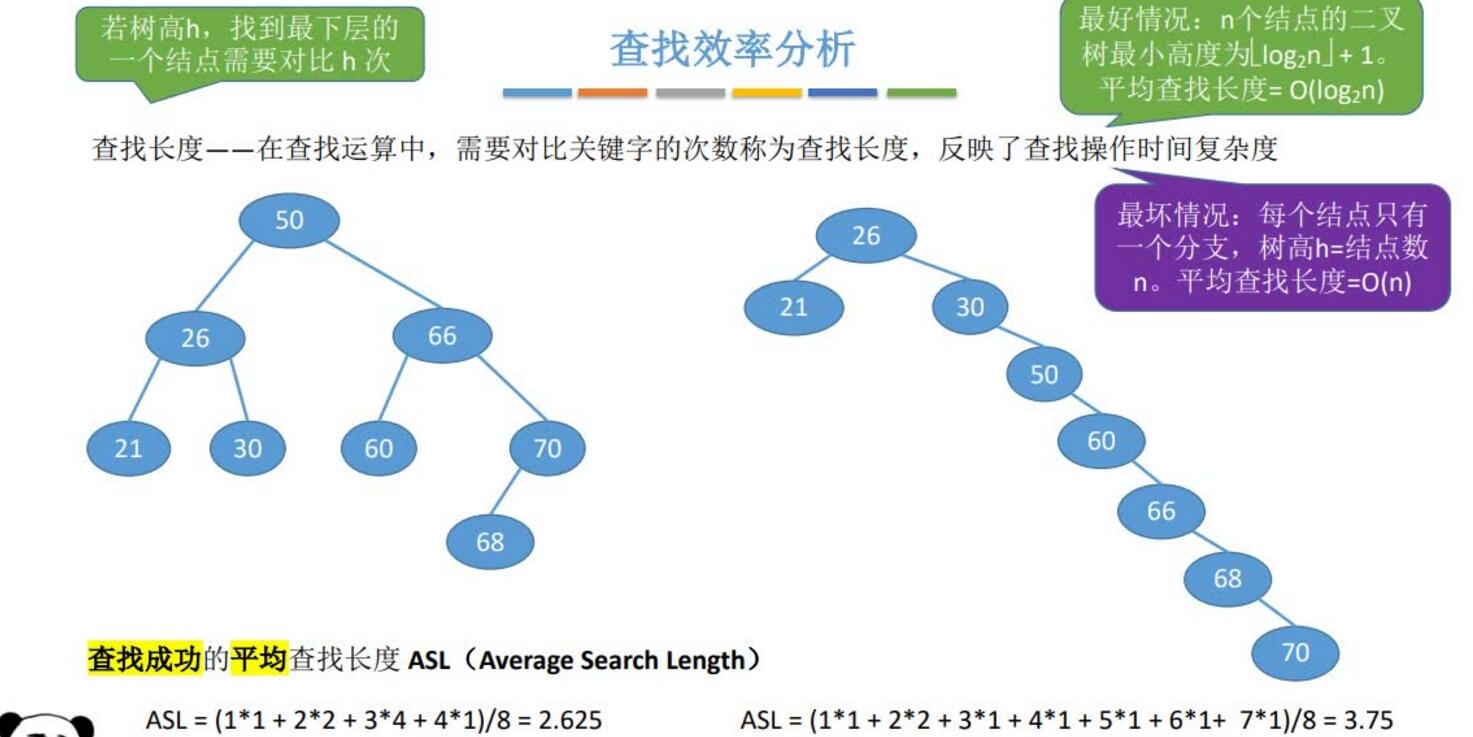
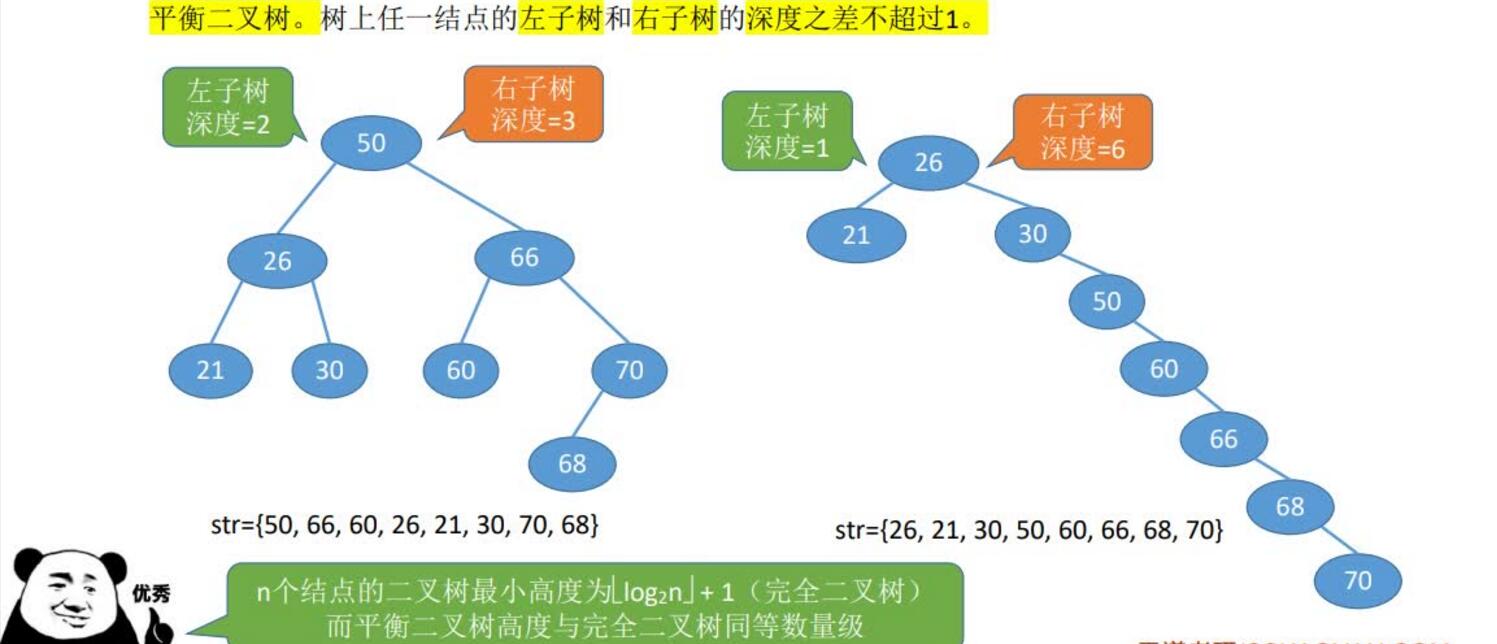
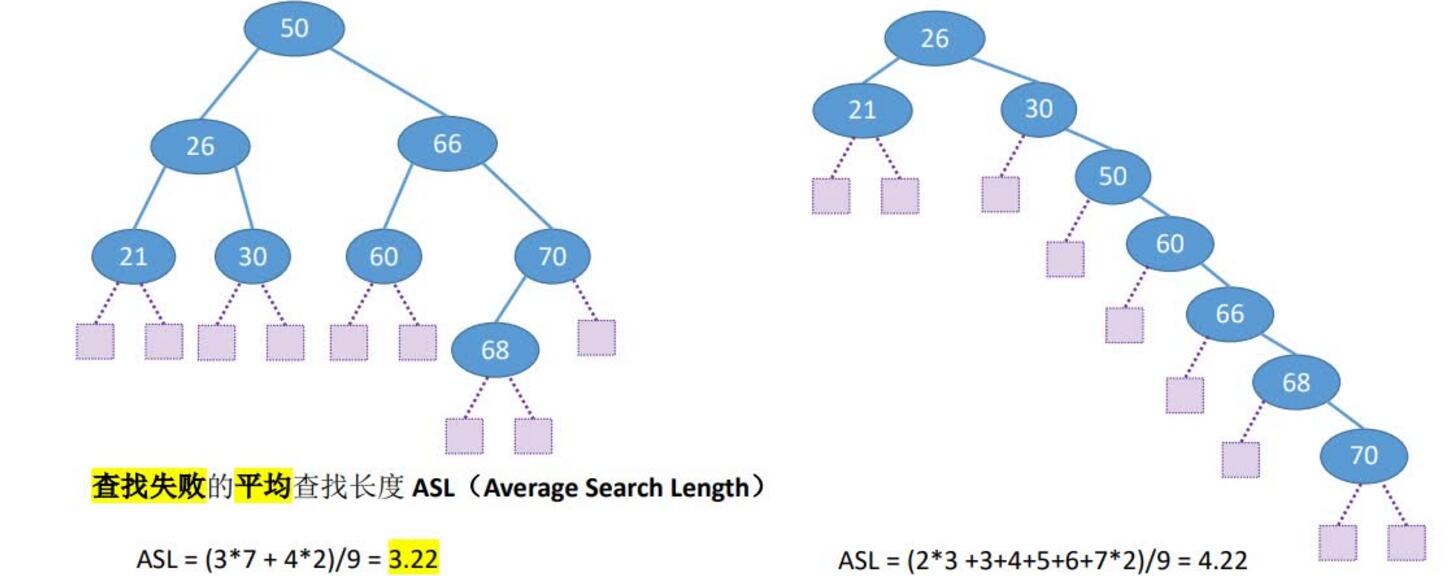
查找长度——在查找运算中，需要对比关键字的次数称为查找长度

二叉排序树总结：

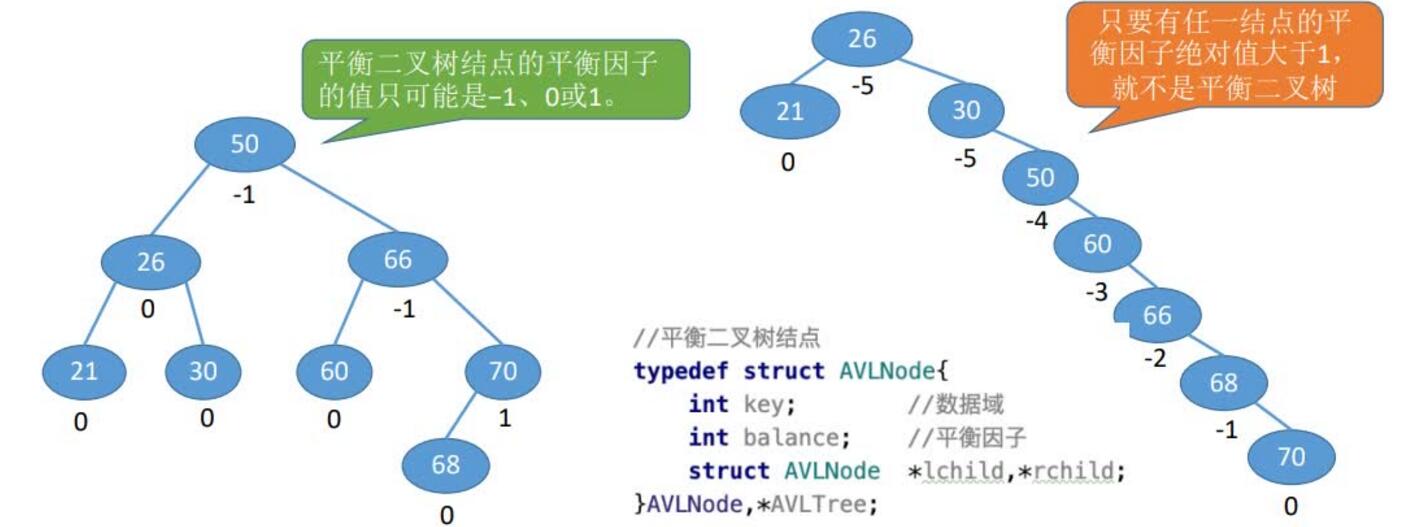
平衡二叉树：

定义：

平衡二叉树（Balanced Binary Tree），简称平衡树（AVL树）—树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子=左子树高-右子树高

插入：
从插入点往回找到第一个不平衡结点，调整以该结点为根的子树
每次调整的对象都是“最小不平衡子树”
在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡

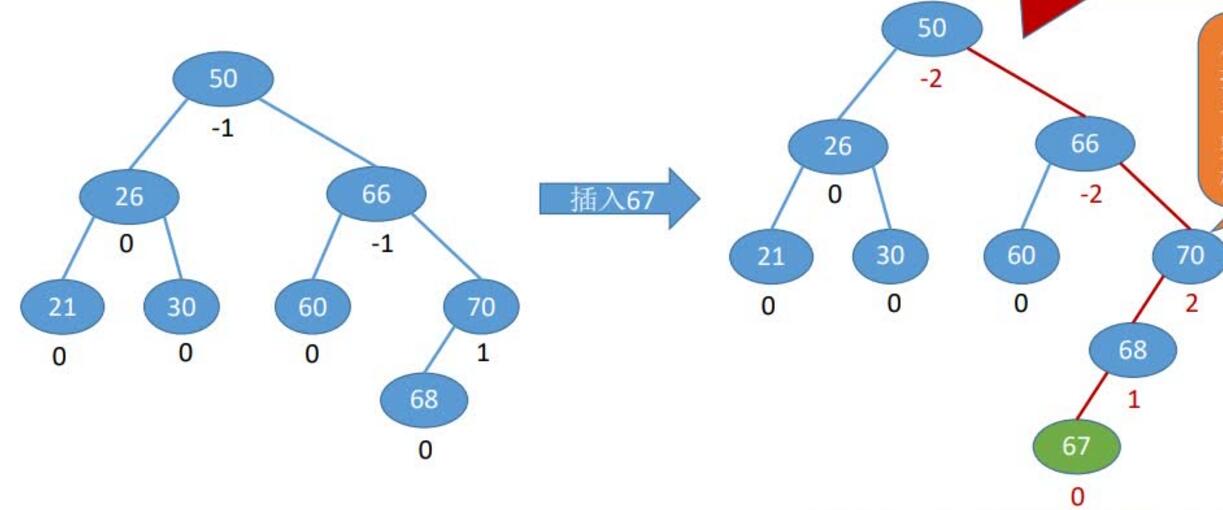
调整：

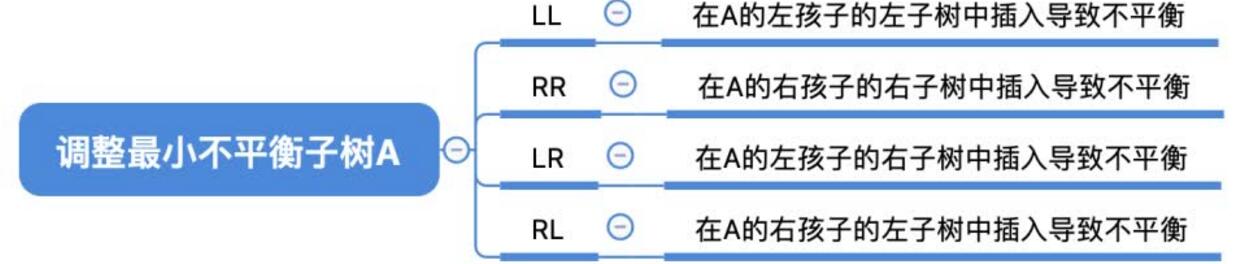
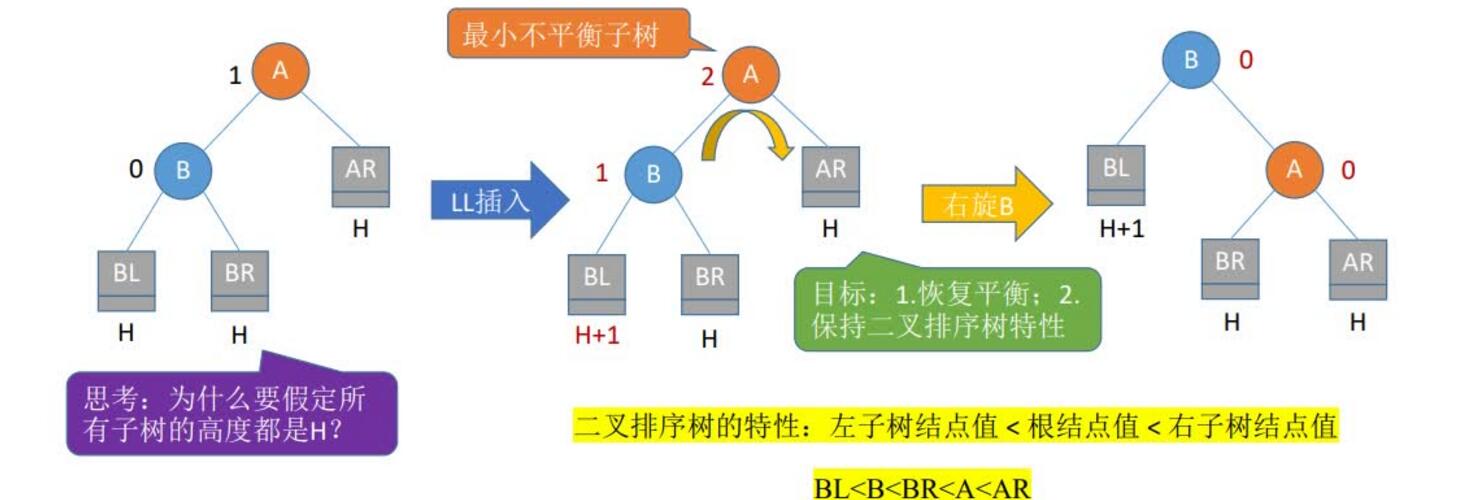
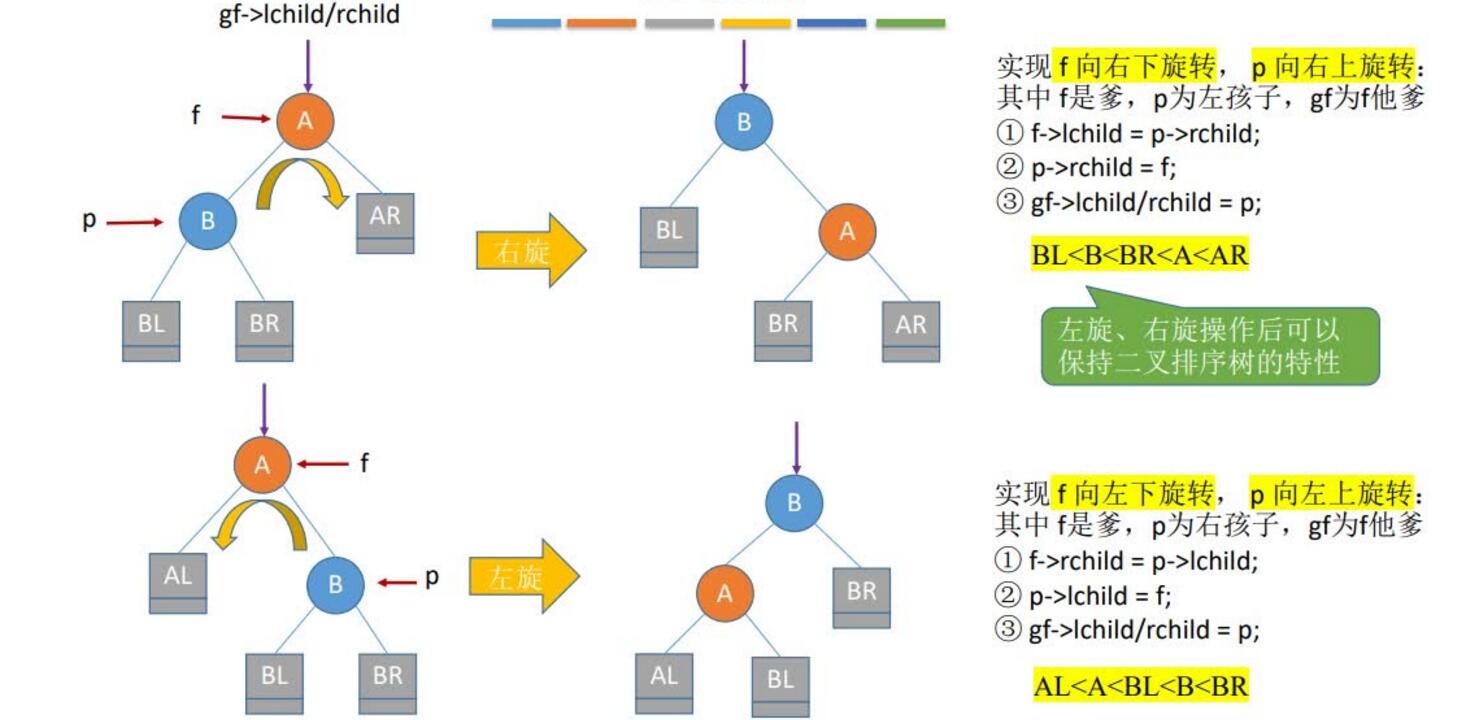
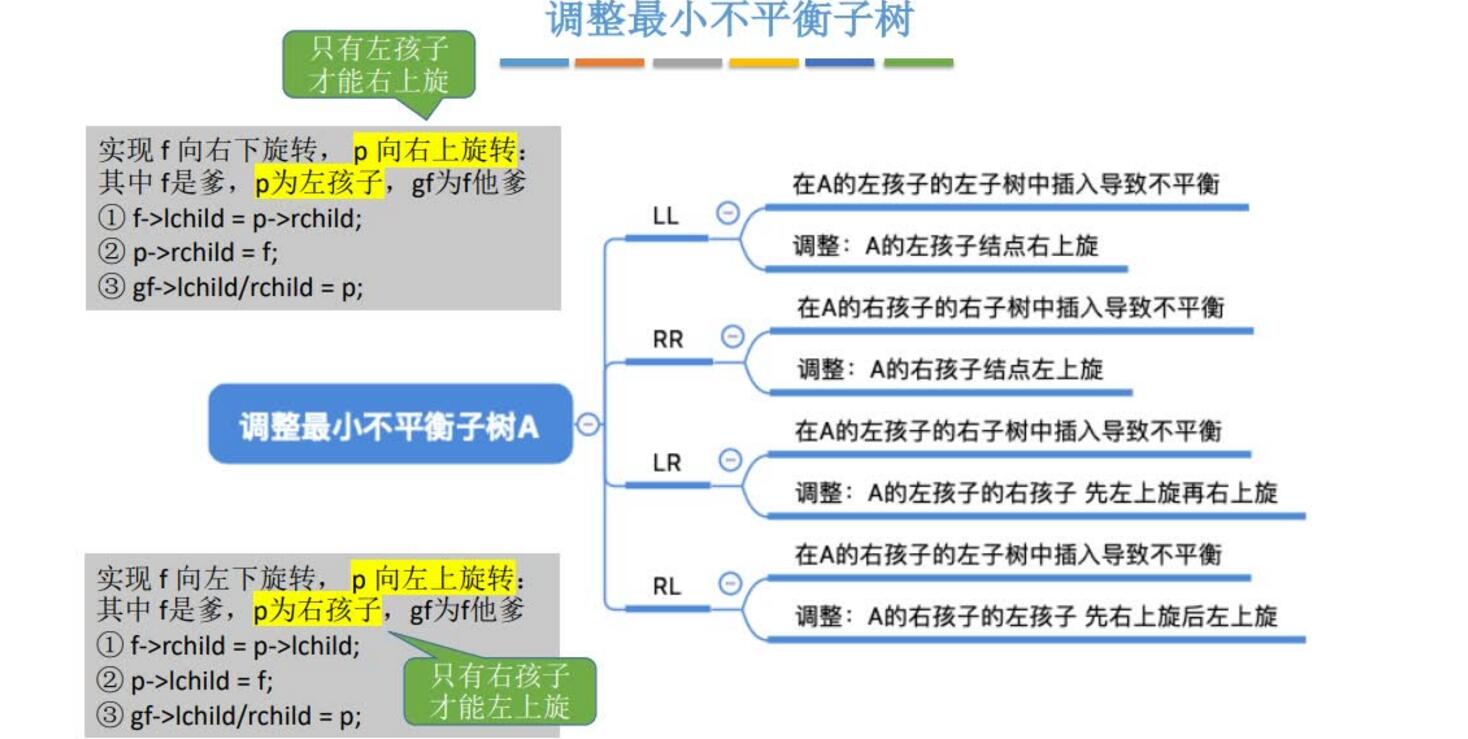
1.LL平衡旋转（右单旋转）。由于在结点A的左孩子（L）的左子树（L）上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋成为B的右子树的根结点，而B的原右子树则作为A结点的左子树

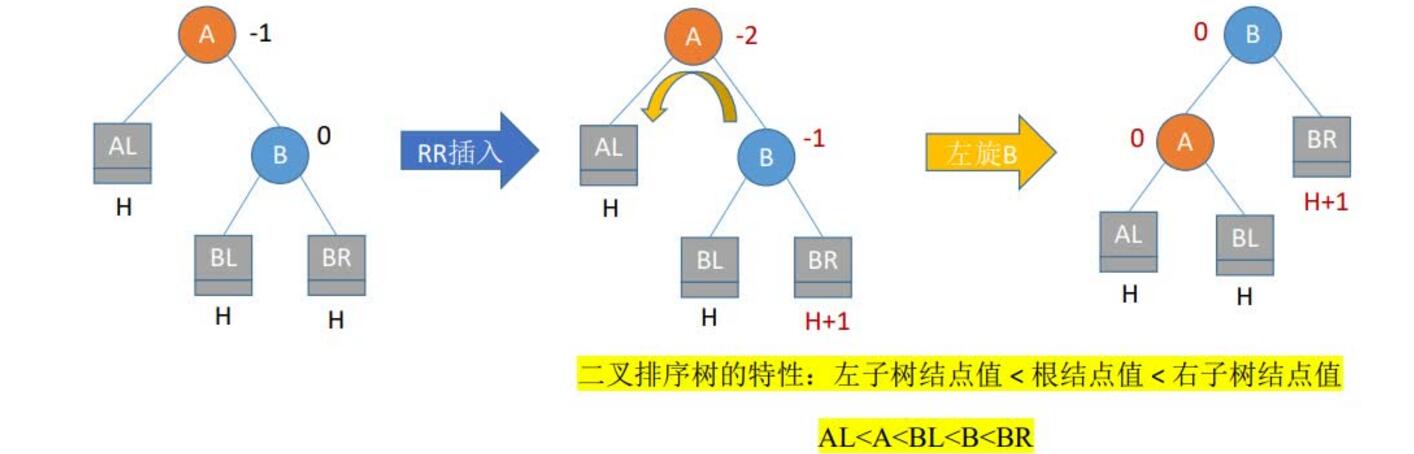
2.RR平衡旋转（左单旋转）。由于在结点A的右孩子（R）的右子树（R）上插入了新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树

代码思路：

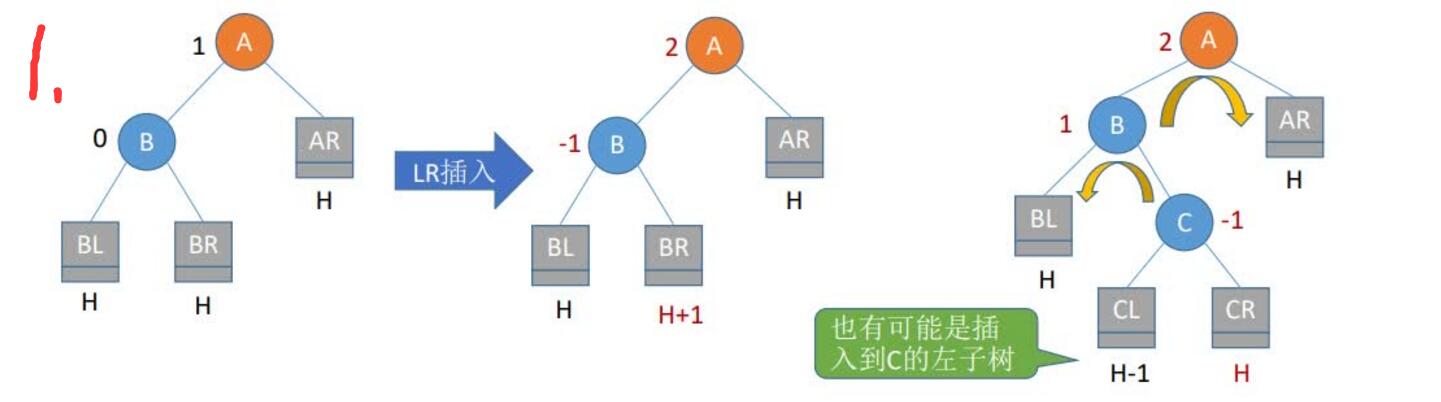
3.LR平衡旋转（先左后右双旋转）。由于在A的左孩子（L）的右子树（R）上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置

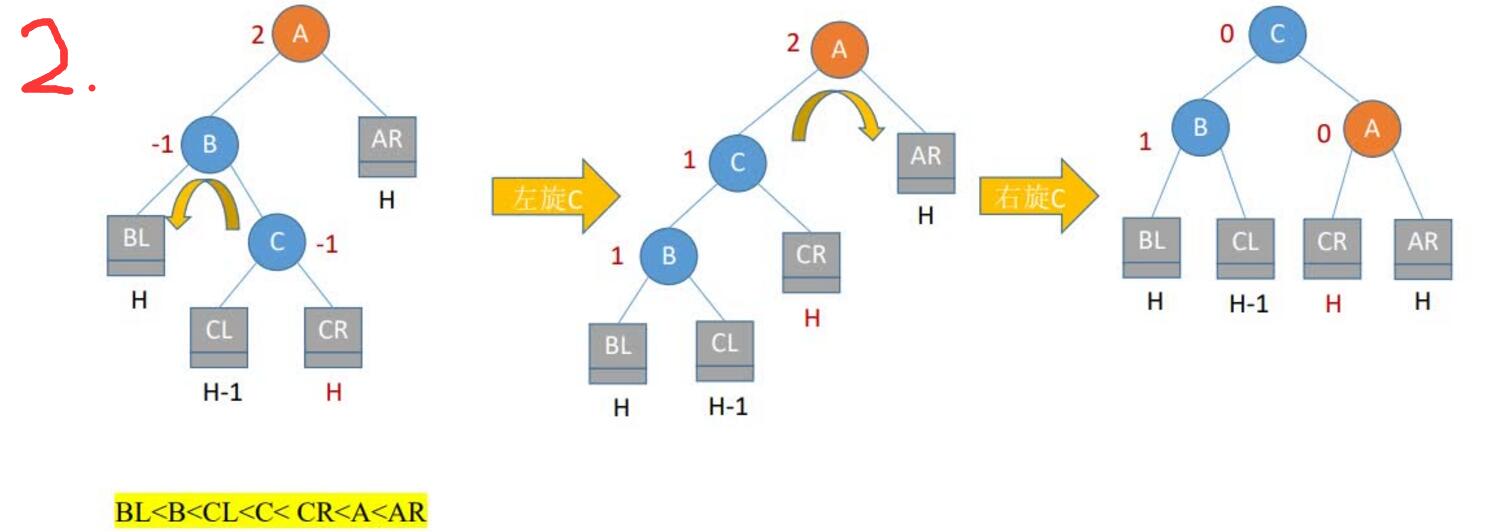
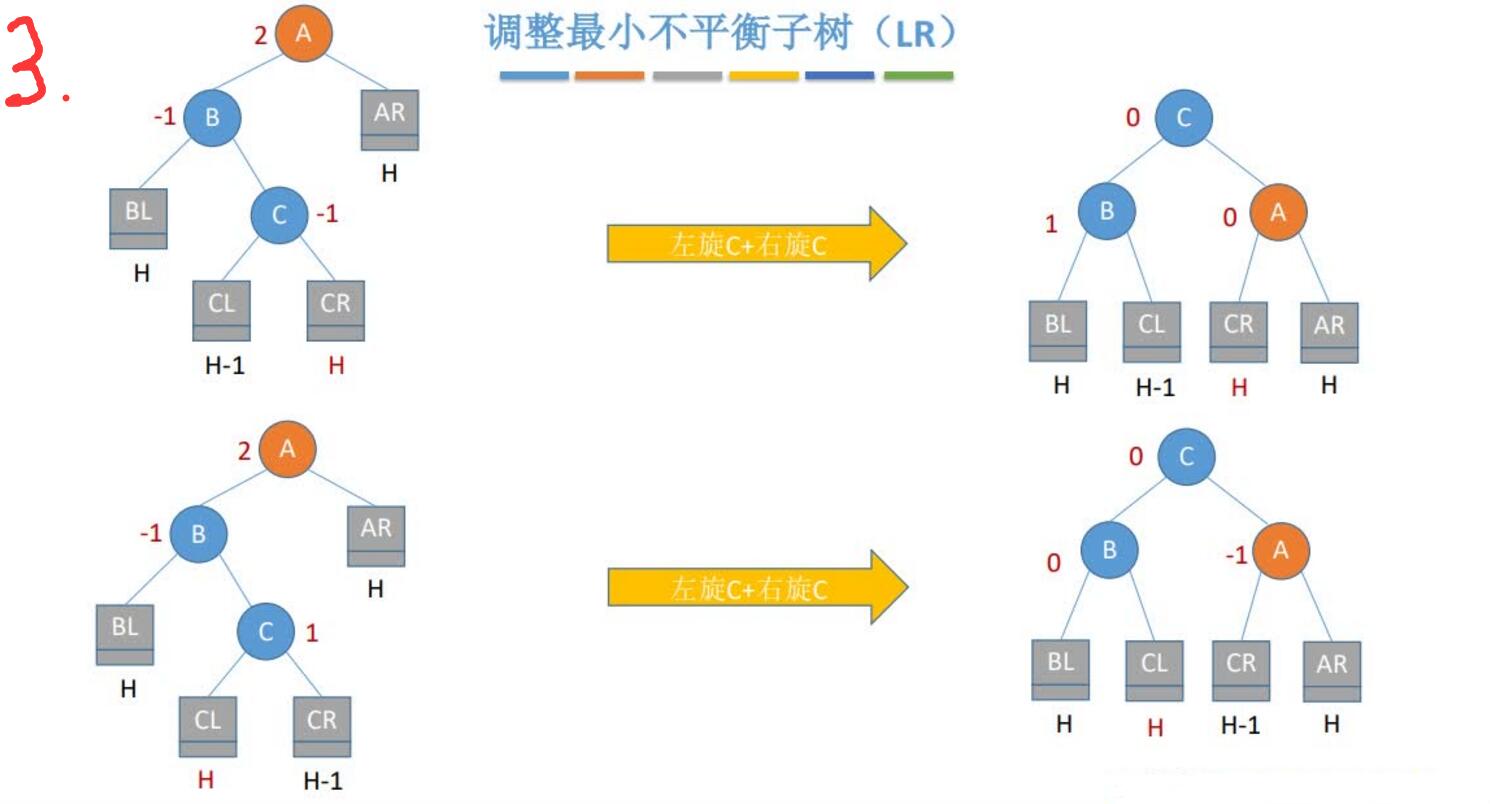
4.RL平衡旋转（先右后左双旋转）。由于在A的右孩子（R）的左子树（L）上插入新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置

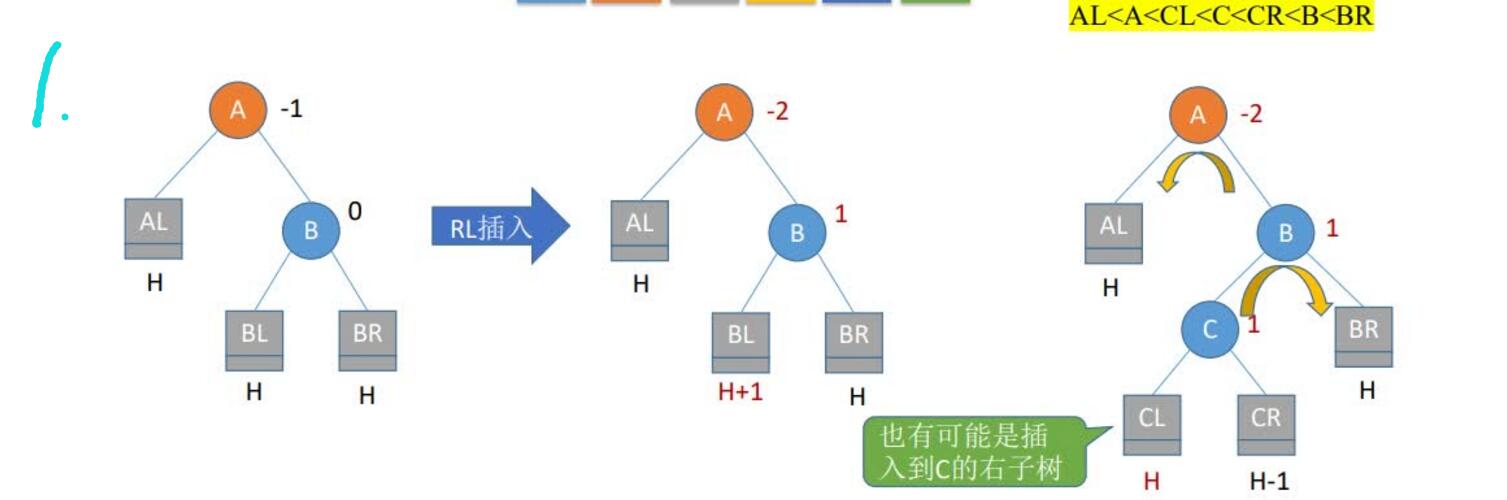
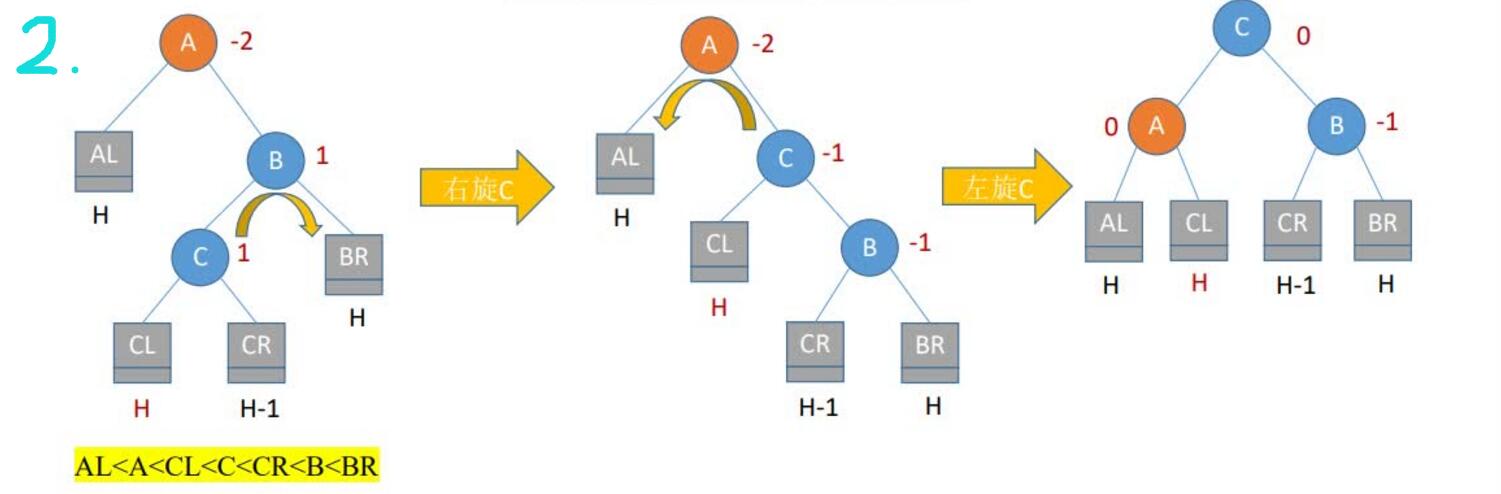
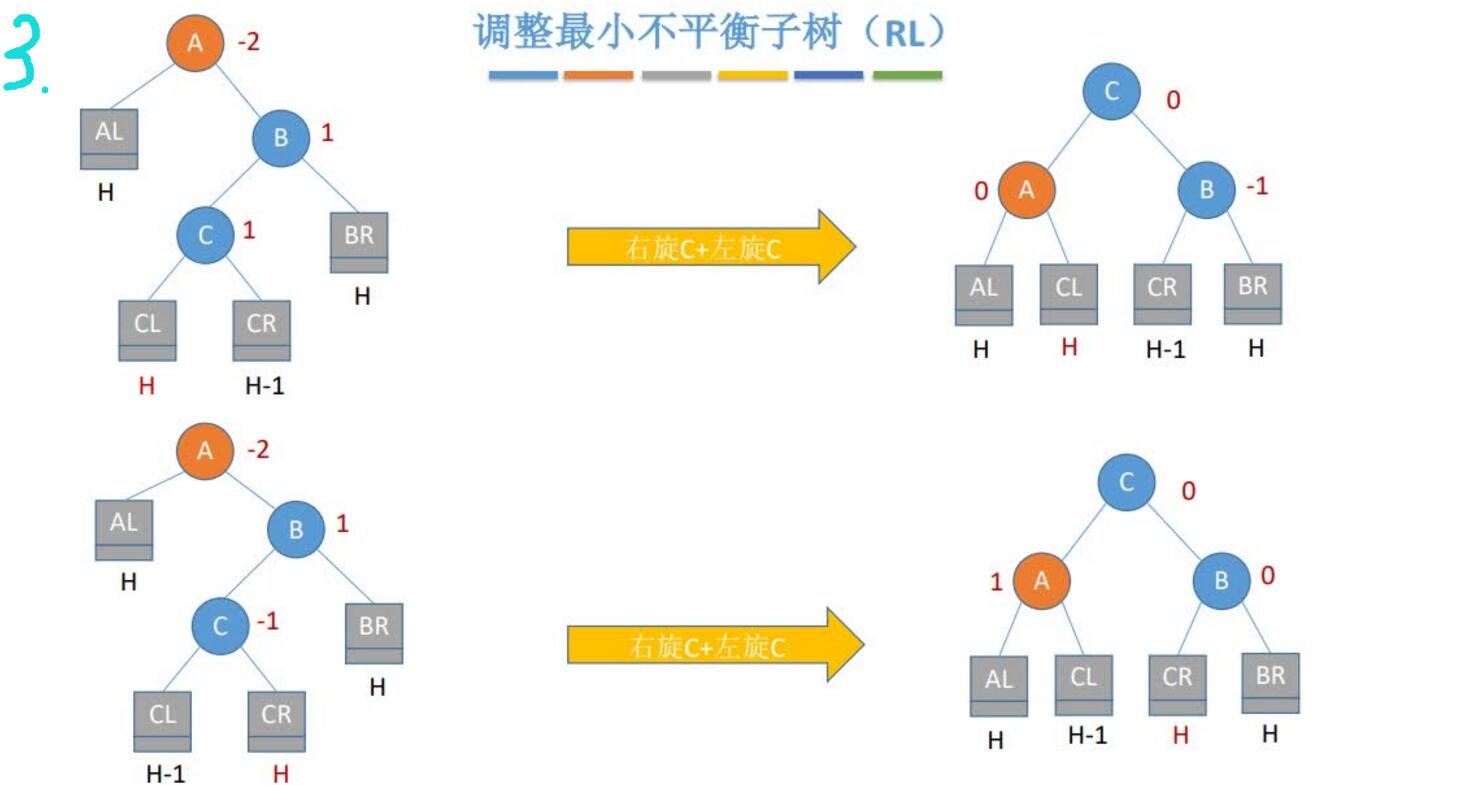
总结：

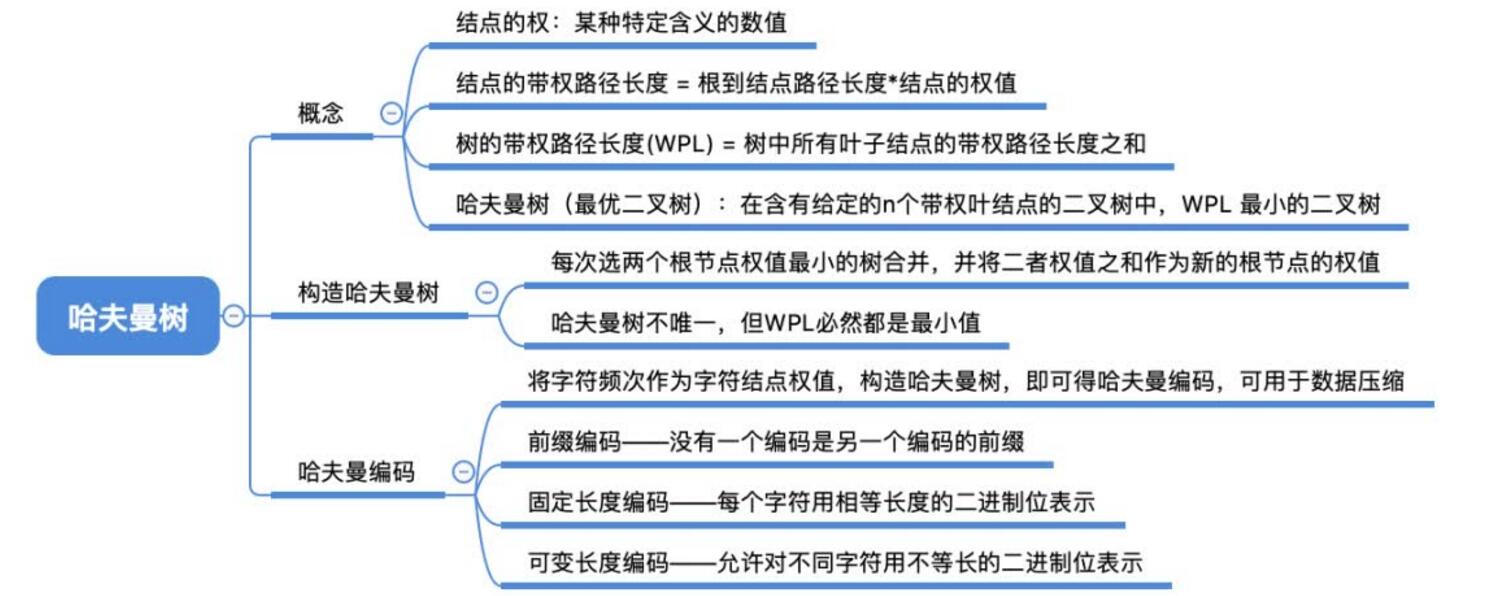
哈夫曼树：

定义：

在含有n个带权叶结点的二叉树中，其中带权路径长度（WPL）最小的二叉树称为哈夫曼树，也称最优二叉树

有关概念：

哈夫曼树的构造：

给定n个权值分别为w1,w2,…,wn的结点，构造哈夫曼树的算法描述如下：
（1）将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。
（2）构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和。
（3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
（4）重复步骤（2）（和3），直至F中只剩下一棵树为止。

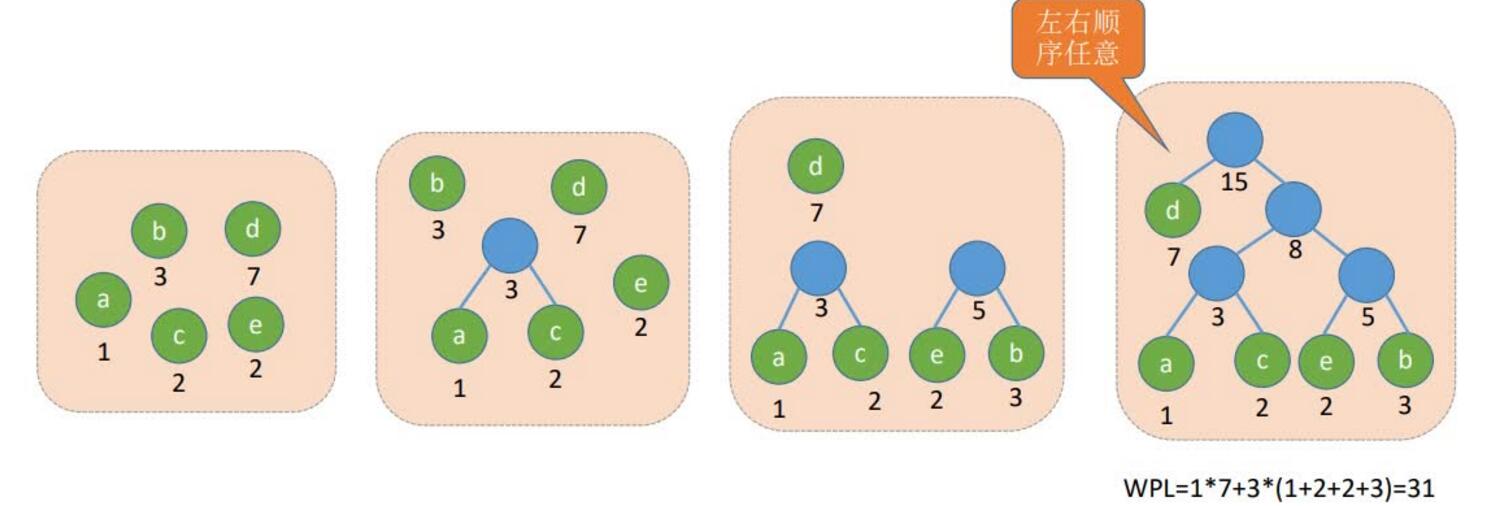
（1）每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大
（2）哈夫曼树的结点总数为2n− 1
（3）哈夫曼树中不存在度为1的结点。
（4）哈夫曼树并不唯一，但WPL必然相同且为最优

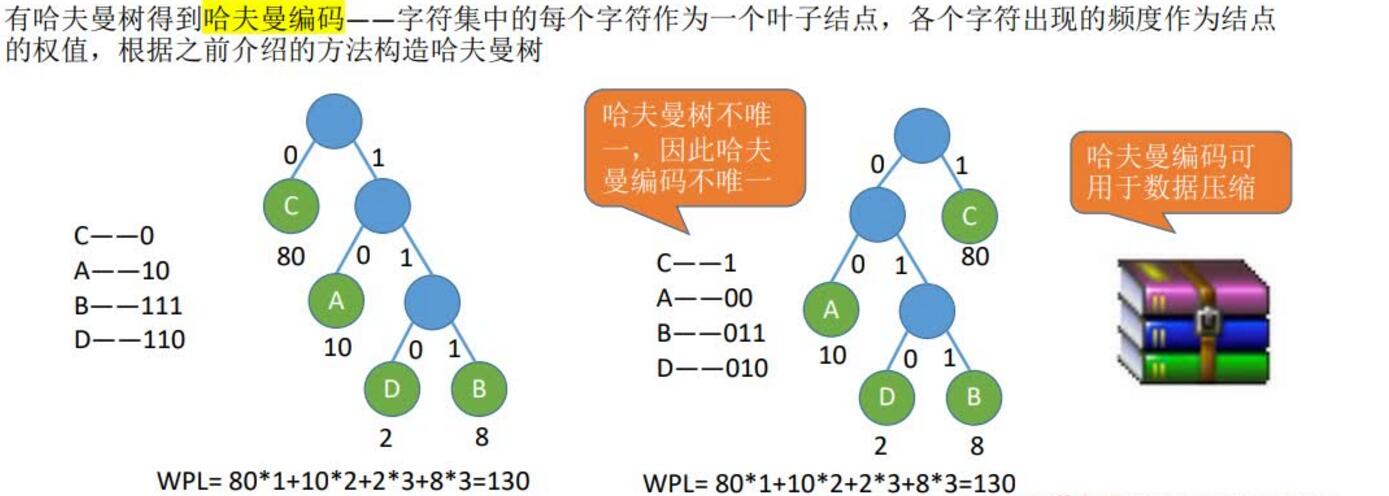
哈夫曼编码：

固定长度编码——每个字符用相等长度的二进制位表示
可变长度编码——允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码

———————————————————————————————————————————（树章节完）