今天晚上参加了网易游戏暑期实习的在线笔试，一共3道题，时限150分钟。

题目1

用 $n \times n$ 的中心对称且轴对称的瓷砖铺满 $m \times m$的墙，$n,m$均是奇数，且$n\le20, m\le200$，要求铺满后的图案也是中心对称且轴对称的。瓷砖边缘部分可以任意裁剪。
输入数据有$T$组，$T\le20$。

输入格式

第一行输入一个$T$，表示有$T$组数据。
对于每组数据，第一行输入$n$和$m$
接下来有$n$行$n$列字符，表示瓷砖的图案，每个字符表示一个中心对称且轴对称的图案。

输出格式

对于每组数据，输出$m$行$m$列字符，表示最终墙的图案。
每组数据的答案用空行隔开。

样例

输入：
2
3 5
|o|
o|o
|o|

5 11
**o**
**o**
ooooo
**o**
**o**


输出：
||o||
||o||
oo|oo
||o||
||o||

ooooooooooo
o****o****o
o****o****o
o****o****o
o****o****o
ooooooooooo
o****o****o
o****o****o
o****o****o
o****o****o
ooooooooooo

算法

(刷数组) $O(n^2)$

由于$m, n$都是奇数，所以我们可以先把一个瓷砖放在墙的正中心的位置，然后顺次在其周围铺满瓷砖，最后再把边缘多出的部分裁剪掉，这样得到的图案一定是中心对称且轴对称的。

现在我们来求一下裁剪前的图案的边长$M$：
当我们放好中心瓷砖后，该瓷砖左边到墙边的距离是$l = (m - n) / 2$，所以左边需要放 $\lceil l/n \rceil$个瓷砖，同理右边也需要放 $\lceil l/n \rceil$个瓷砖，所以$M = n + \lceil l/n \rceil * 2n$。
在C++中，整数相除默认是下取整，因此我们要将上取整的计算转化为下取整的计算：
$$ \lceil l/n \rceil = \lfloor (l + n - 1) / n \rfloor $$
所以最终有

int M = n + ((m - n) / 2 + n - 1) / n * n * 2;

然后我们再求每个边界需要裁剪的距离$gap = (M - m) / 2$。

计算好这些数据之后：

1. 我们先通过两重循环，将$n \times n$的数组刷到$M \times M$的数组里，表示铺满瓷砖的过程；
2. 输出的时候，我们在首尾各保留$gap$的距离，表示裁剪的过程；

C++ 代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

char tile[25][25];
char wall[260][260];

int main()
{
    int T, n, m;
    cin >> T;
    while (T--)
    {
        cin >> n >> m;
        for (int i = 0; i < n; i++) cin >> tile[i];
        int M = n + ((m - n) / 2 + n - 1) / n * n * 2;
        for (int i = 0, ii = 0; i < M; i++, ii = (ii + 1) % n)
            for (int j = 0, jj = 0; j < M; j++, jj = (jj + 1) % n)
                wall[i][j] = tile[ii][jj];
        int gap = (M - m) / 2;
        for (int i = gap; i < M - gap; i++)
        {
            for (int j = gap; j < M - gap; j++)
                cout << wall[i][j];
            cout << endl;
        }
        cout << endl;
    }
    return 0;
}

题目2

一个足球队要招募最少 $X$ 个前锋和 $Y$ 个后卫，现在有 $n$ 个备选球员，每个球员有两个属性值 $s_{0}, s_{1}$，

• $s_{0}表示$当前锋的能力值
• $s_{1}$表示当后卫的能力值

一个球员最多只能身兼一个职位。一个球队的能力值被定义为所有前锋和后卫的能力值的最小值。问球队的能力值最大是多少？

输入格式

第一行一个 $T$，表示共有 $T$ 组数据，$(T\le20)$
对于每组数据，第一行输入 $n, X, Y$，表示共有 $n$ 备选个球员，球队最少招募 $X$ 个前锋以及 $Y$ 个后卫，$(n, X, Y \le 10000)$，
接下来 $n$ 行，每行两个数，表示$s_{0}, s_{1}$，$0 \le s_{0}, s_{1} \le 10000$

输出格式

对于每组测试数据，输出一个数，表示球队能力值的最大值。

样例

输入：
2
4 2 1
1 4
2 3
3 2
4 1

5 2 2
1 4
2 5
6 2
4 6
2 4

输出：
3
4

算法

(二分查找+贪心) $O(nlogn)$

这道题目让我们求最小值的最大值，是典型的二分查找类型的题目。

首先我们二分出一个球队的能力值level，然后判断level是否能被满足（也就是判断在level下，能否招满 $X$ 个前锋和 $Y$ 个后卫）：

• 如果level能被满足，则增加level的值
• 如果level不能被满足，则降低level的值

然后我们考虑如何判断一个level是否能被满足。首先，我们遍历所有球员，将球员分为四大类：

1. 仅能达到前锋的要求，则直接招入成前锋；
2. 仅能达到后卫的要求，则直接招入成后卫；
3. 既能达到前锋的要求，也能达到后卫的要求，则加入待选集合；
4. 前锋和后卫的要求都达不到，则直接淘汰；

然后我们求出前锋和后卫共缺多少人，如果缺的人数 $\le$ 待选集合人数，则说明level可以被满足；否则level不能被满足。

C++ 代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010;

int n, X, Y;
int s0[N], s1[N];

bool check(int level)
{
    int x = 0, y = 0, s = 0;
    for (int i = 0; i < n; i++)
    {
        bool can_x = s0[i] >= level, can_y = s1[i] >= level;
        if (can_x && !can_y) x++;
        else if (!can_x && can_y) y++;
        else if (can_x && can_y) s++;
    }
    return max(0, X - x) + max(0, Y - y) <= s;
}

int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n >> X >> Y;
        int l = 0, r = 0;
        for (int i = 0; i < n; i++)
        {
            cin >> s0[i] >> s1[i];
            r = max(r, s0[i]);
            r = max(r, s1[i]);
        }
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1;
        }
        cout << r << endl;
    }
    return 0;
}

题目3

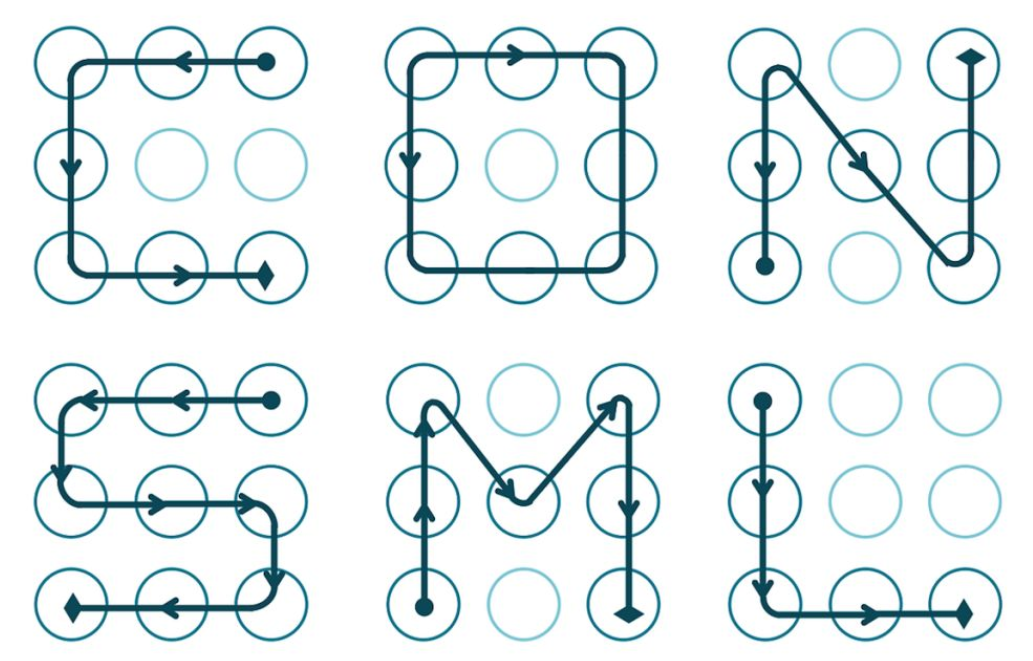
如上图所示，这道题让我们求$3*3$的手机解锁手势的方案数。有几个细节需要注意：

1. 手势滑动时可以穿过其它点
2. 线路可以重叠，但使用的端点不允许重复
3. 线路要求至少包含两个点
4. 线路形状相同即视为同一种方案，不论方向是否相同、线路是否重叠。比如 假设第一行三个点从左到右依次编号是1， 2， 3：则1 -> 3、3 -> 1、1 -> 3 -> 2、1 -> 2 -> 3这四种线路均视为同一种方案。
5. 图中有些点可以用，有些点不可用，’.’表示可用，’X’表示不可用，详情见样例输入。

输入格式

第一行一个 $T$，表示共有 $T$ 组数据，$(T\le20)$
对于每组数据，输入一个 $3*3$ 的矩阵，表示图中哪些点可用，哪些点不可用

输出格式

对于每组测试数据，输出一个数，表示方案数

样例

输入：
3
...
XXX
XXX
...
XXX
X.X
.X.
X.X
.X.


输出：
3
22
111

算法

(DFS+哈希) $O(9!)$

这道题的难点在于如何判断两个路线的形状是否相同。我们先对所有点做如下编号：
0 | 1 | 2
3 | 4 | 5
6 | 7 | 8

我们现在来考虑如何在C++中表示一个“线路的形状”，一个“形状”由若干线段组成，线段一共有 $9 * 8 / 2 = 36$ 种，我们用0-35对其编号。
其中有些线段是重叠的，比如(0, 1)、(1, 2) 和 (0, 2)是重叠的，为了避免这种情况，我们将某些线段去掉：如果一个线段可以由两个更短的线段连接而成，则将其去掉。

此时，一个“形状”可以唯一地表示成一些线段的集合，两个“形状”相同当且仅当它们对应的线段的集合相同。

在C++中，我们可以用一个long long类型的变量表示线段的集合：如果集合包含某种线段，假设线段的编号是 $x$，则在long long类型变量的二进制表示中，将第 $x$ 位置成1，如果不包含，则置成0。

然后我们在DFS过程中，维护一个long long类型的变量state，表示当前线路的“形状”。我们每加入一条新的边，就将state相应的二进制位置成1。
最后我们用哈希表对state判重。

C++的标准库中实现了哈希表：unordered_set<T>，可以直接用，不需要自己实现。

C++ 代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_set>

using namespace std;

char g[3][3];
bool st[9];
int id[9][9];

inline long long edge(int a, int b, int c, int d)
{
    int x = a * 3 + b, y = c * 3 + d;
    if (x > y) swap(x, y);
    return 1ll << id[x][y];
}

void dfs(int x, int y, unordered_set<long long>&hash, long long state)
{
    if (state) hash.insert(state);

    for (int i = 0, k = 0; i < 3; i++)
        for (int j = 0; j < 3; j++, k++)
        {
            if (st[k] || g[i][j] == 'X') continue;
            long long nstate = state;
            if ((i + x) % 2 == 0 && (j + y) % 2 == 0)
            {
                int mx = (i + x) / 2, my = (j + y) / 2;
                nstate |= edge(i, j, mx, my);
                nstate |= edge(mx, my, x, y);
            }
            else
            {
                nstate |= edge(i, j, x, y);
            }
            st[k] = 1;
            dfs(i, j, hash, nstate);
            st[k] = 0;
        }
}

int main()
{
    for (int i = 0, k = 0; i < 9; i++)
        for (int j = i + 1; j < 9; j++, k++)
            id[i][j] = k;
    int T;
    cin >> T;
    while (T--)
    {
        for (int i = 0; i < 3; i++) cin >> g[i];
        unordered_set<long long> hash;
        for (int i = 0, k = 0; i < 3; i++)
            for (int j = 0; j < 3; j++, k++)
                if (g[i][j] == '.')
                {
                    st[k] = 1;
                    dfs(i, j, hash, 0);
                    st[k] = 0;
                }
        cout << hash.size() << endl;
    }
    return 0;
}