时间复杂度 $o(n^2)$ 。 适用于稠密图 和 边权值非负的图。
算法流程：

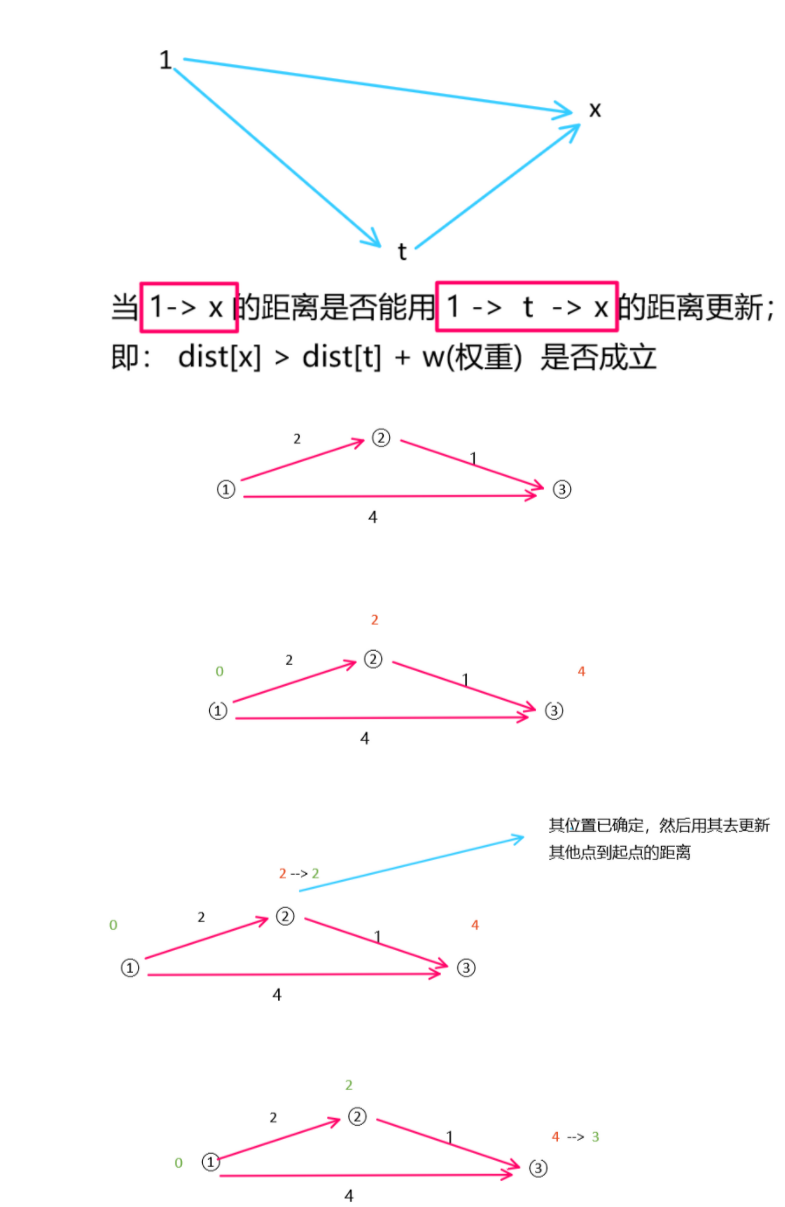
1：初始化 dist[1] = 0 ,其余节点正无穷大。

2：找出一个未标记的，dist[x] 最小的节点 x ，然后标记节点 x。

3： 扫描节点 x 的所有出边 (x ,y, z) ，若 dist[y] > dist[x] + z,则使用 dist[x] + z 更新 dist[y].

4：然后重复 2~3 步骤，直到所有节点被标记。

bool st[N]; //  标记数组，用于该点已经被用过去更新最短路，当前点到起点的最短路已确定。
int dist[N];//  最短路数组

void Dijkstra()
{
    //  初始化距离    
    memset(dist,0x3f,sizeof dist);
    memset(st, 0 , sizeof st);
    //  初始化最短路的起点的距离
    dist[1] = 0; 

    // 遍历寻找 n - 1 次
    for(int i = 1 ; i < n ; i++){
        int x = -1;

        //  这里遍历的目的是要找到未标记 节点中 dist 最小的
        for(int j = 1 ; j <= n ; j++)
      // 未被使用去更新其他点 &&  (未在已更新的最短路上 || 当前距离大于可以被更新的距离)
            if(!st[j] && (x == -1 || dist[x] > dist[j])) 
                x = j; //  符合条件，替换

        if(x == n) break; // 如果找到，直接返回

        st[x] = true; // 当前点的最短路已确定。（已被用过去更新其他点）

        //  用全局最小值 去更新其他节点。
        for(int y = 1 ; y <= n ; y++)
            // 用 1 到 x 距离 + x到j的这条边来更新到 j 最短路
            dist[y] = min(dist[y],dist[x] + g[x][y]); 
    }
}

/*
1:关于 memset(dist, 0x3f,sizeof dist)
    memset 是按照字节来进行初始化， 我们这里的 int 是 4 个字节  
    所以初始化之后的  dist[N] 中的元素是  0x3f3f3f3f。

2:起点初始不能被标记。即 st[1] = 1 不写;

因为 标记数组 的作用就是当这个点的已经被用去更新其他点后,该点到起点的最小值已经被确定,
但如果初始时就已经 st[1] = 1,那么就会导致不能进入循环更新最短路，从而不进行 Dijkstra的过程

上述疑惑的原因主要是 来源于 spfa 算法的  st[] 数组，spfa 算法中的 st[] 数组指的是
该点是否在队列中, 而非最短路已确定。

*/

堆优化Dijkstra 算法

用小根堆优化 Dijksra 算法。
时间复杂度 $o(mlogn)$ 。 适用于 稀疏图，用邻接表存图。
朴素 Dijkstra 算法中寻找最小的 dist 是将所有的边都遍历一遍，这需要 $o(n)$ 时间复杂度。
可以使用小根堆去优化。小根堆会将最小值置于堆顶，而小根堆自身堆调整将最小值置于堆顶的时间复杂度是 $o(logm)$
(因为是完全二叉树)
c++ 中直接使用 priority_queue 去实现小根堆。
注意：
priority_queue<PII , vector<PII> , greater<PII>> heap; 是二元组，并且采用 greater<PII> 这个比较器，
其先按照第一关键字进行排序，所以必须将 距离 dist 作为第一关键字。 即 heap.first = dist 。

int dijkstra(){
    memset(dist,0x3f,sizeof dist);
    memset(st , 0 , sizeof st);

    dist[1] = 0;

    // 使用优先队列来维护距离，小根堆
    priority_queue<PII,vector<PII>,greater<PII>> heap;   
    heap.push({0,1}); // 起点入队

    while(heap.size()){
        auto t = heap.top(); // 取出堆中 表示距离最小的点
        heap.pop(); 

        int ver = t.second,distance = t.first; // ver 是编号， distance 是距离
        if(st[ver]) continue;  // 说明这个点之前出现过，直接过

        st[ver] = true; // 优化操作，可以减少每次的判点数量

        for(int i = h[ver] ; i != -1 ; i = ne[i]){  // 再用当前的点来更新最短路
            int j = e[i];
            if(dist[j] > distance + w[i]){   // 如过当前距离大于之前的 距离就更新
                dist[j] = distance + w[i];
                heap.push({dist[j],j});   // 再将 j 这个点放到优先队列中
            }
        }
    }

    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}