算法提高课汇总

强联通分量 $Strongly\;Connected\;Components,\;SCC$

什么是强联通分量

• 联通分量: 有向图中, 对一个联通分量中的任意两点$u, v$($u$可能等于$v$), 一定存在$u\rightarrow v$和
  $v\rightarrow u$的路径.

• 强联通分量: “极大”联通分量 — 如果在某个联通分量中加入任意不在该联通分量的一个顶点后,
  该分量不再联通, 则称这个联通分量为强联通分量.

$SCC$的应用

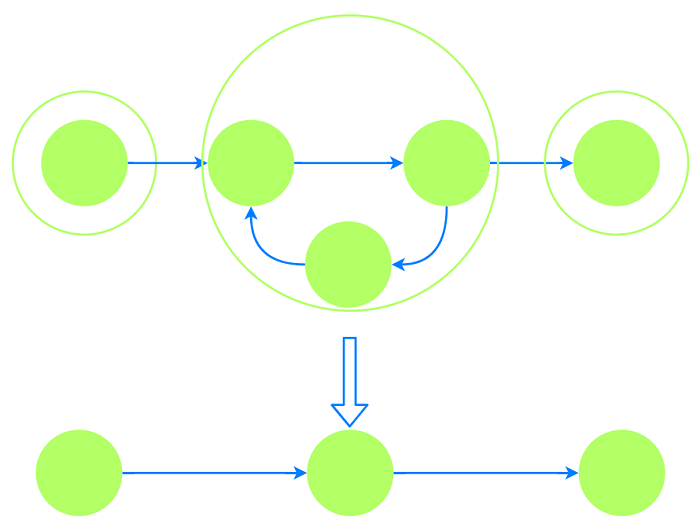
对于任意一个强联通分量, 对于其中任意两点$u, v$存在路径$u\rightarrow v$与$v\rightarrow u$, 存在至少一个环.
而强联通分量之间不存在环, 否则可以合成一个联通分量. 因此如果我们对每个强连通分量进行
缩点操作, 则新图一定是一个有向无环图($DAG$, 也称拓扑图).

有向图拥有更简单的结构, 对某些问题可以用相对简单的算法求解.

缩点操作: 同一强联通分量内的顶点视为一个顶点, 只保留不同强联通分量之间的边.

$Tarjan$求强联通分量

$dfs$中的$4$类边

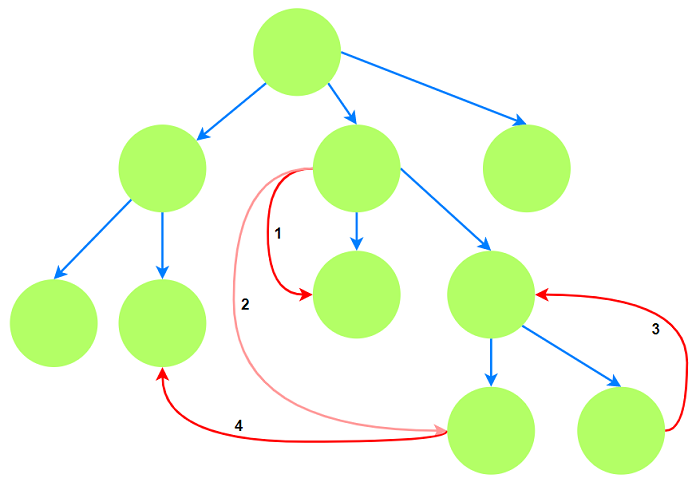
如果我们在图中按$dfs$的顺序建立一颗树(深度搜索树), 这颗树存在$4$类边:

1. 树枝边: 树(深度搜索树)边.

2. 前向边: $u$指向自己子孙$v$的边. 树枝边可以认为是前向边的一种特殊情况.

3. 后向边: $v$指向自己的祖先$u$的边, 是图中存在联通分量的关键.

4. 横叉边: $u$指向左边分支节点$v$. 不存在指向右边, 否则其顺序恰好是$dfs$遍历顺序, 即树枝边.

$Tarjan$算法思想

在有向图中如何形成一个联通分量:

1. 顶点$u$存在后向边.

2. 顶点$u$存在横插边指向$v$, 而$v$的后续边指向$u$的祖先节点.

$Tarjan$算法具体实现

引入时间戳概念, 对每个顶点记录两个时间戳:

• $dfn(u)$: $dfs$执行过程中, 顶点$u$被访问的时间.

• $low(u)$: 顶点$u$经过后续节点可以到达的最小时间点.

此外通过栈保存: 已经被$dfs$访问且还未找到对应$SCC$的顶点.

判断$SCC$: 对于顶点$u$, 若$dfn(u) == low(u)$, 则从栈顶到$u$的顶点均属于同一$SCC$.

• $dfn(u) == low(u)$可以理解为从$u$出发经过某些环最后到达自身, 且不能到达其他祖先节点.

• 从栈顶到$u$均属于同一$SCC$: 假设存在顶点$v$在栈中且不属于当前$SCC$, 设顶点$v$对应强联通分量
  代表节点为$v’$(即$dfn(v’) == low(v’)$), 则$dfs$顺序只能是$u\rightarrow v’\rightarrow v$, 算法保证
  当回溯至$v’$时, 会将$v$出栈, 所以假设不成立.

一个简单例子

假设原图如下所示:

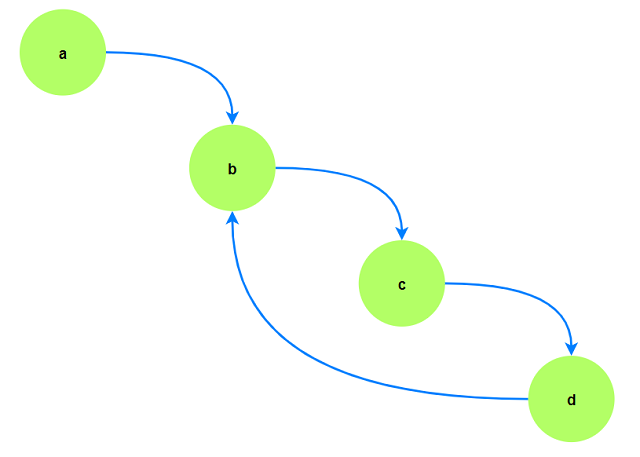
$tarjan$算法基于$dfs$, 访问顺序为$a\rightarrow b\rightarrow c\rightarrow d$, 对应$(dfn, low)$与栈内元素如下图:

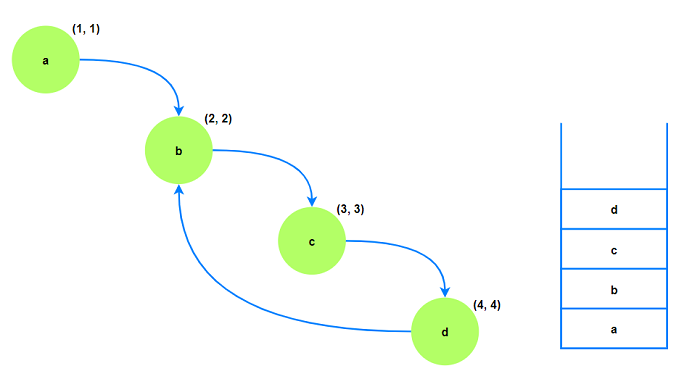
当算法到达$d$时, 由于$d$存在指向$a$的后向边且此时$a$仍在栈中, 所以$low(d)$可更新为2.

对于$c$节点, 其到达的子节点$d$可以到达的最小时间戳为2, 所以$low(c)$可更新为2. $b$同理.

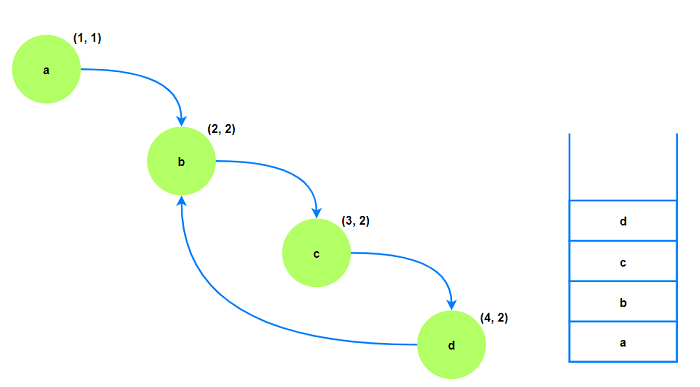
对于$b$节点, 其不存在可以到达更早节点的后向边, 或可能到达更早节点的横叉边, 所以$low(b)$不能继续更新,
此时$dfn(b) == low(b)$, 找到一个强连通分量, 将$d\sim b$出栈.

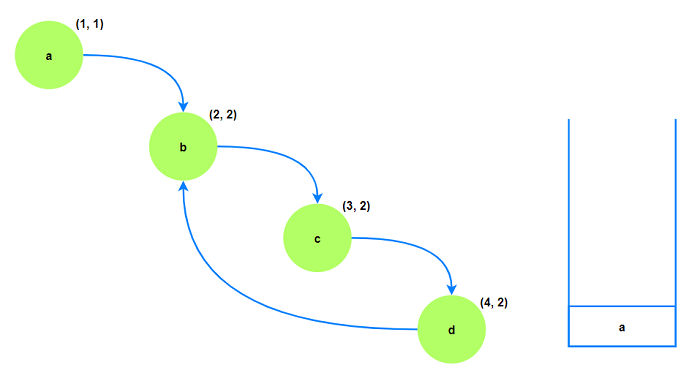
对于节点$a$, 其不存在额外的边, $dfn(a) == low(a)$, $a$作为一个节点数目为1的强联通分量出栈.

算法细节

• 在$low(u)$更新过程中, 不考虑已经遍历且出栈节点$v$: 已出栈说明节点$v$属于其他强联通分量, 与$u$独立.

• 在$low(u)$更新过程中, 对于已遍历且仍在栈中的节点$v$, 用$low(v)$还是$dfn(v)$更新? 都可以, 算法在
  节点回溯时才会更新对应$low$值, 对于节点$v$还没回溯, $low(v)$还未更新, 所以此时$dfn(v) == low(v)$.