笔记内容来源于算法基础课

贪心

证明

证明：贪心解$=$最优解

1. 贪心解劣于最优解，必成立
2. 贪心解好于最优解，通常使用调整法：将最优解调整到贪心解后，可以得到更优的结果

反证法

数学归纳法

区间问题

1. 左端点排序
2. 右端点排序
3. 双关键字排序

右端点排序，一般使用$f(1, i)$；左端点排序，一般使用$f(i, n)$

Huffman 树

合并树表示为一棵完全二叉树，即每个节点都有两个子节点

叶子节点为需要合并的节点，其它节点为合并产生的中间节点

$W = \sum \limits_{i=1}^{n} w_i l_i$

最终合并的结果可以发现，需要合并的节点与它的深度相关。因此应当使权值大的节点尽可能靠近根节点，权值小的节点尽可能远离根节点。

所以可以使用最小堆，每次选择最小的两个节点，再将新构成的节点重新插入到堆中，直到堆中只剩一个节点。

排序不等式

$W = \sum \limits_{i=1}^{n} (n - i) a_i$

根据公式，总结果与数所处的位置相关。因此应当使数值越小的数越靠近前面。

绝对值不等式

$|x-a| + |x - b| \ge |a - b|$

可以通过数轴上$x$的范围进行分类讨论来证明

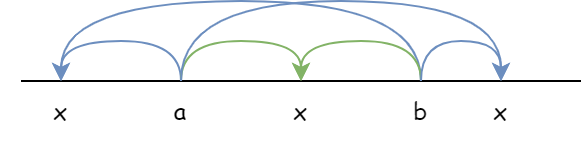
对于数轴上的多个点$x_1, x_2, \cdots , x_n$，则可以排序后进行分组再使用不等式

$|x - x_1| + |x - x_2| + \cdots + |x - x_n| = |x - x_1| + |x - x_n| + |x - x_2| + |x - x_{n-1}| \ge |x_1 - x_n| + |x_2 - x_{n-1}| \cdots$

等号成立当且仅当所有不等式的等号均成立，因此：

1. 当$n$为偶数时，则必须满足 $x_{\frac{n}{2}} \le n \le x_{\frac{n}{2}}+1$
2. 当$n$为奇数时，则必须满足 $x = x_{\frac{n}{2} + 1}$

所以当$x = x_{\frac{n}{2} + 1}$时，便可以同时满足奇数和偶数的情况

Arrays.sort(a, 0, n);
int res = 0;
for (int i = 0, j = n - 1; i < j; i++, j--) res += a[j] - a[i]; // a[n/2] 为目标点

推公式

推公式的技巧一般为将同属于$i$的放在一起

Acwing 125 根据公式确定最优解的形式

Acwing 3728 经典公式

Acwing 3771 推公式