算法提高课汇总

差分约束

啥是差分约束

差分约束是包含$m$个不等式, 包含$n$个变量的形如:

$$\begin{cases} x_{i_1}\le x_{i_2} + c_{i_1} \\\\ x_{i_2}\le x_{i_3} + c_{i_2} \\\\ …\\\\ x_{i_{n-1}}\le x_{i_n} + c_{i_{n-1}} \end{cases}$$

的不等式组.

差分约束与最短路

下面将从两方面介绍差分约束如何用最短路算法求解:

1. 用最短路算法求不等式组的一组可行解.

2. 用最短路算法求可行解的最值.

$1.\;$求可行解

建图

观察不等式组中的不等式: $x_i\le x_j + c_i$, 其形式类似于最短路中的三角不等式$dist[i]\le dist[j] + w$.
我们可以对每个不等式建立一条对应的有向边:

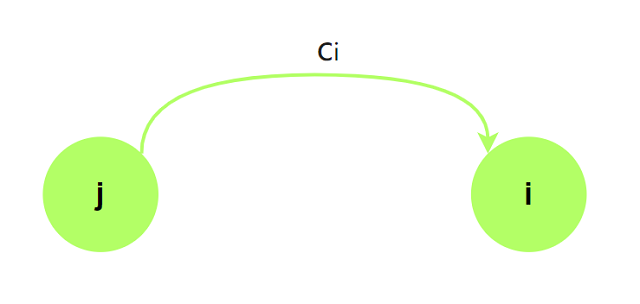
若原图不存在负环, 则经过最短路算法后对于每个有向边都有$dist[i]\le dist[j] + w$, 否则$dist[i]$的值
在算法过程中会被更新. 即经过最短路算法后$dist$值可以作为原不等式组的一组可行解.

也就是通过将每个不等式与对应有向边一一对应, 我们将差分约束转换为最短路问题.

注意

单源最短路的源点需要满足的条件:

• 从源点$s$出发必须保证可以经过图上所有的有向边. 即保证算法考虑不等式组中的所有不等式.

存在负环

上述转换过程一直强调原图中不存在负环, 若图中存在负环, 对应到不等式组存在何种情况?

假设存在负环:

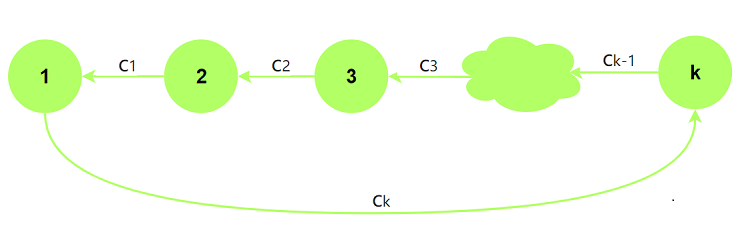
对应不等式:

$\;\;\;\;x_1\le x_2+c_1, x_2\le x_3+c_2, … , x_k\le x_1+c_k$ -->
$\;\;\;\;x_1\le x_3+c_1+c_2$ --> $x_1\le x_k+c_1+c_2+…+c_{k-1}$ --> $x_1\le x_1+\sum c$
$\;\;\;\;$因为$\sum c\lt 0$ -->$x_1\lt x_1$.

也就是若原图存在负环, 说明原不等式组可以通过上述不等式链的形式推导出自相矛盾的结果. 即若图中
存在负环, 说明原不等式组无解.

最短路求可行解小结

求解过程:

1. 将所有不等式组转换为有向边.

2. 找一个满足条件的源点$s$.

3. 求单源最短路.

结果:

1. 若存在负环, 说明原不等式无解.

2. 否则我们找到一组可行解.

源点$s$需要满足的条件: 从源点出发可以经过所有有向边.

最长路求可行解

最长路即将最短路算法某些计算过程翻转. 经过最长路算法后, 满足不等式$dist[v]\ge dist[u] + w$,
我们可以将上述不等式转换为$x_j\ge x_i - c_i$, 对应有向边:

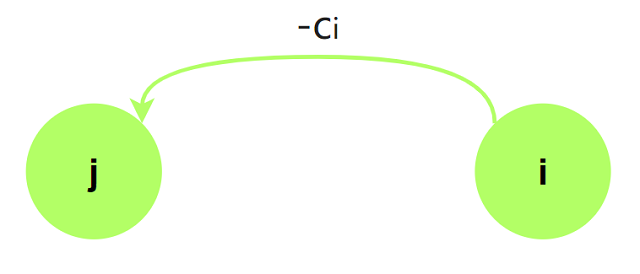
注意: 若原图存在正环, 说明原不等式无解. 其他的计算过程与最短路相同.

$2.\;$求最值

先以求最大值为例 — 最大值指的是所有可行解均取其最大值.

最求大值的前提是不等式组中至少存在一个不等式满足: $x_i\le c_i$, 也就是至少存在一个变量
有明确上界; 否则所有不等式组表示的是变量的相对关系, 这种情况下在得到一组可行解后, 我们
让所有可行解同时$+c$, 变量相对关系不变, 即可行解有无数个, 不存在最值.

在图中实现明确上界

首先一个问题是如何将不等式$x_i\le c$转变为有向边 — 只有一个顶点的边. 可以建立一个虚拟
源点$s$指向$x_i$, 边权为$c$. 源点$s$取确定值$0$, 则满足不等式$x_i\le s + c, s = 0$ --> $x_i\le c$.

最短路求最大值

考虑从源点到地点$u$的一条路径与不等式的关系:

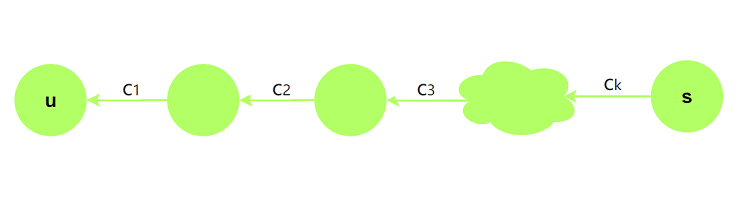
通过缩放我们知道$dist[u]\le c_1 + c_2 + … + c_k + s(=0)$. 即$s\rightarrow u$的一条路径上的边权和
可以转化为一条不等式链, 因为存在点有明确上界(转化为$s = 0$), 所以通过$s\rightarrow u$的一条路径
我们得到了$dist[u]$的一个上界, 而$dist[u]$的值最大可以取所有上界的最小值 — 对应于图中所有$s$到$u$
的路径的最短路径. 所以通过最短路算法我们可以得到可行解的最大值.

最长路求最小值

类似的思路, 每条$s\rightarrow v$的路径对应于$dist[u]$的一个下界, 而$dist[u]$的最小值可以取所有
下界的最大值 — 对应图中所有$s\rightarrow u$路径的最长路径.