最小生成树
对于无向连通图$G$, $G$的一颗生成树$T$是包含$G$所有顶点的树. 树中各边
的权值之和$W(T)$称为树的权, 具有最小权的生成树称为$G$的最小生成树.
生成树性质
设$G$是有$n$个顶点的联通图:
-
$T$是$G$的生成树当前仅当$T$无环且有$n - 1$条边.
-
如果$T$是$G$的生成树, 存在不在$T$内的边$e\notin T$, 则么$T\cup \lbrace e\rbrace$含有一个环$C$.
-
去掉
2.加入的环$C$的任意一条边, 就得到了另外一颗生成树$T’$.
生成树性质的应用
最小生成树算法:
- 算法步骤: 选择边.
- 约束条件: 不形成回路(生成树必要条件).
- 截止条件: 边数达到$n - 1$.
改进生成树$T$的方法:
- 在$T$中加一条非树边$e’$, 形成回路$C$, 在$C$中去掉一条边$e$, 形成一颗新树$T’$.
$W(T’) - W(T) = W(e’) - W(e)$. 若$W(e’)\le W(e)$, 则$W(T’)\le W(T)$.
求最小生成树
贪心法:
- $Prim$ 算法
- $Kruskal$ 算法
$Prim$ 算法
设计思想
假设图$G = (V, E, W), V = \lbrace1, 2, …, n\rbrace$:
- 初始$S = {1}$, (可以是任意顶点)
选择连接$S$与$V - S$的最短边$e = \lbrace u, v\rbrace$, 其中$u\in S, v\in V-S$.
将$e$加入$T$, $v$加入$S$.
重复上述过程, 直到$S = V$为止.
(从一个初始连通块不断向外扩张, 类似$Dijkstra$算法思路).
正确性证明: 归纳法
证明的思路是对步数进行归纳, 每一步的正确性用反证法.
证明: 对于任意$k\lt n$, 存在一颗最小生成树包含算法前$k$步选择的边.
-
归纳基础: $k = 1$, 存在一颗最小生成树$T$包含边$e = \lbrace 1, u\rbrace$, 其中$\lbrace 1, u\rbrace$是所有关联$1$的边中
权最小的边. (算法选择的边). -
归纳步骤: 假设算法前$k$步选择的边构成一颗最小生成树的边, 则算法前$k + 1$步选择的边也构成一颗
最小生成树的边.
归纳基础
证明: 存在一颗最小生成树$T$包含算法第一步选择的边 — 关联节点$1$的最小权的边$e = \lbrace 1, u \rbrace$.
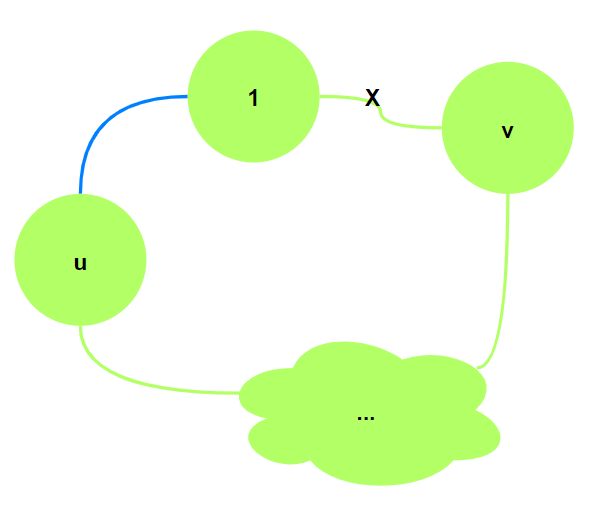
- 证: 设$T$为一颗最小生成树, 假设$T$不包含${1, u}$, 则$T\cup \lbrace \lbrace 1, u\rbrace \rbrace$含有一条回路, 回路中
关联$1$的另一条边$\lbrace 1, v\rbrace$. 用$\lbrace 1, u\rbrace$替换$\lbrace 1, v\rbrace$得到树$T’$, 则$T’$也是生成树, 且$W(T’)\le W(T)$.(算法保证第一次选择的边$\lbrace 1, u\rbrace$的权值最小)
如果原生成树$T$是最优的, 而$W(T’)\le W(T)$, 所以$T’$也是最优的, 且包含算法第一步选择的边. 所以归纳基础正确.
归纳步骤
假设算法进行了$k$步, 生成树的边为$e_1, e_2, …,e_k$, 这些边的端点构成集合
$S$. 由归纳假设存在$G$的一颗最小生成树$T$包含这些边.
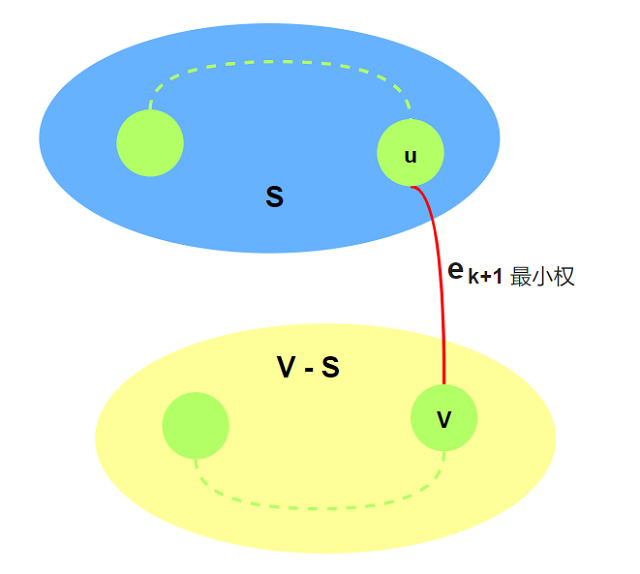
算法第$k + 1$步选择$e_{k + 1}$ — 从当前$S$到$S - V$权值最小的边. 若$e_{k+1}\in T$, 算法第$k + 1$步
显然是正确的.
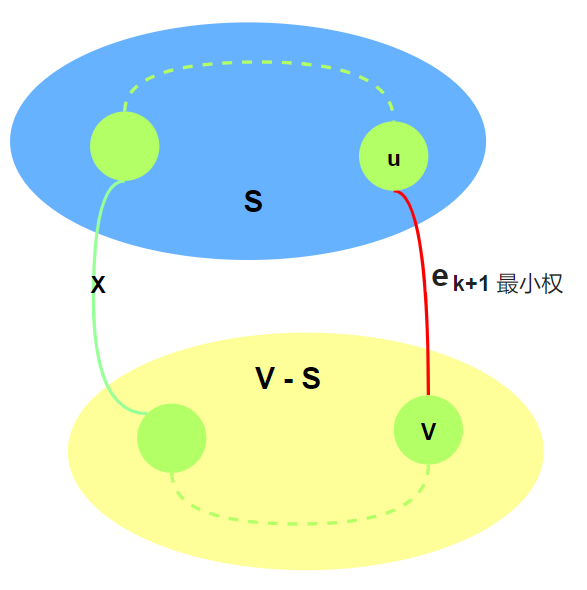
若$e_{k + 1}\notin G$, 则将$e_{k+1}$加到$T$中形成一条回路. 这条回路有另外一条边$e$连接$S$与$S-V$中的顶点.
去掉$e$得到树$T’$, 算法保证$e_{k + 1}\le e$, 则$W(T’)\le W(T)$. 算法到$k + 1$步仍得到最小生成树.
$Kruskal$算法
设计思想
假设图$G = (V, E, W), V = \lbrace1, 2, …, n\rbrace$:
-
按长度从小到大对边排序.
-
依次考察当前最短边$e$, 如果$e$与$T$的边不构成回路, 则把$e$加入树$T$, 否则跳过$e$.
直到选择$n - 1$条边为止.
正确性证明: 归纳法
证明: 对于任意的$n$, 算法对$n$阶图(包含$n$个顶点的图)可以找到一颗最小生成树.
归纳基础
证明: $n = 2$, 算法正确.
- $G$只有一条边, 直接加入即可. 最小生成树就是图$G$.
归纳步骤
证明: 假设算法对于$n$阶图是正确的, 其中$n\gt 1$, 则对于任意$n + 1$阶图算法也得到
一颗最小生成树.
在开始证明前先介绍在证明中需要用到的短接操作.
- 短接操作: 将图$G$中最小权边$e = \lbrace u, v\rbrace$的两个端点合并成一个顶点, 连接$u, v$的边
均指向合并后的顶点.
例如原图$G$以及最小边权$e$如下:
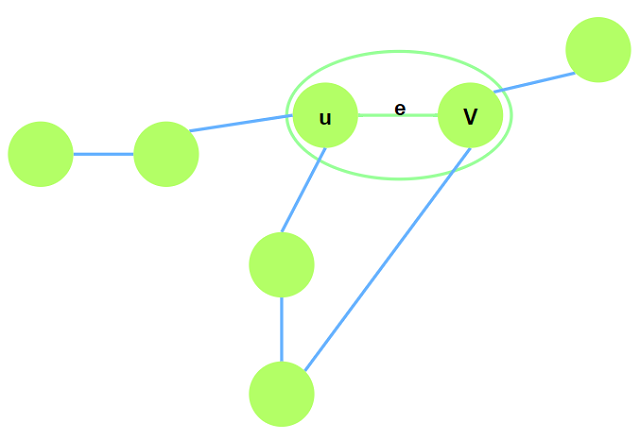
短接$e$:
继续归纳步骤证明:
-
对任意$n + 1$阶图$G$短接最短边$e$, 得到$n$阶图$G’$. 就以上图为例.
-
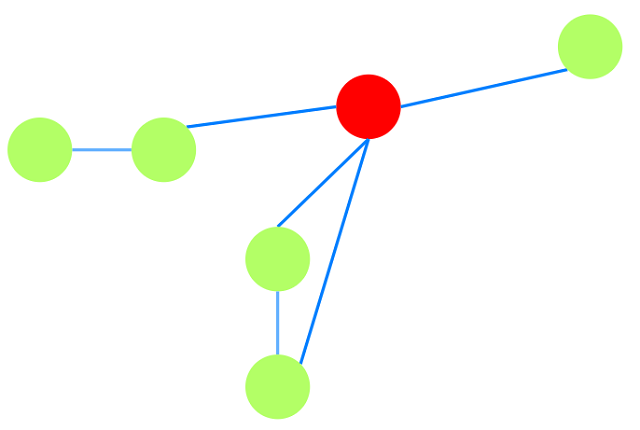
短接操作后, 根据归纳假设, 算法得到$G’$的最小生成树$T’$. 假设图$T’$如下:
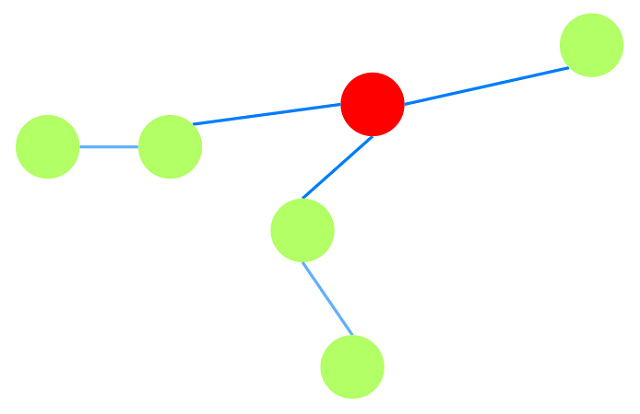
- 为得到原图$G$的最小生成树, 将被短接的边$e$“拉伸”回原来的长度, 得到树$T$.
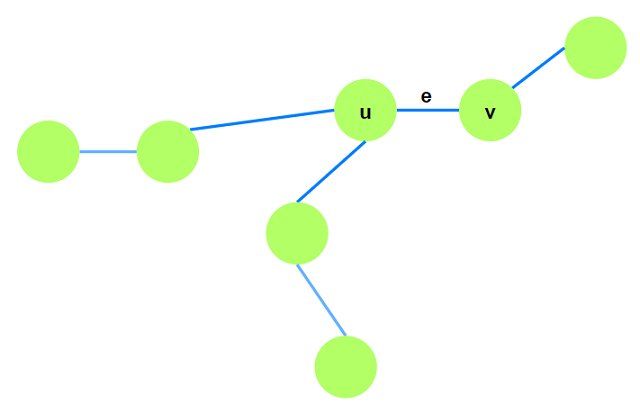
- 树$T$的顶点等于原图$G$的顶点. 证明$T$是$G$的最小生成树. 同样用到$Prim$反证法的思路: 假设
$e\notin T$, 则加上$e$后构成环路$C$, 因为$e$是$G$的最小边权, 所以任意去掉$C$中除$e$以外
一条边, 树的总边权不会增加.

