本笔记内容来源于算法基础课

容斥原理

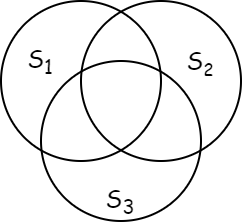
如图，代表了韦恩图(Venn diagram)的一个实例

其中三个集合所包含的所有元素为$S_1 + S_2 + S_3 - S_1 \bigcap S_2 - S_1 \bigcap S_3 - S_2 \bigcap S_3 + S_1 \bigcap S_2 \bigcap S_3$

可以类推到$n$个集合包含的元素,$M_i$代表从$i$个集合取交集的方案数，则所有元素可以$M_1 - M_2 + M_3 + \cdots + (-1)^{n-1} M_n$

最后得到式子所包含的项数为$C_n^1 + C_n^2 + \cdots + C_n^n = 2^n - C_n^0 = 2^n - 1$

证明：

$S_1 \bigcup S_2 \cdots S_n = \sum_i S_i - \sum_{i,j} S_i \bigcap S_j + \cdots$

设存在一个元素$x$存在于$k$个集合当中

左式必然只会统计一次

则右式计算得到的次数为$C_k^1 - C_k^2 + \cdots + (-1)^{k-1} C_k^k = -(1 - 1)^k + C_k^0 = 1$

因此左右元素是一一对应的

实现

由于所有的可能情况为$2^m - 1$，因此一般采用位运算的方式枚举所有可能的情况

选取了$k$个集合，则符号为$(-1)^{k - 1}$，也就是奇数为正，偶数为负

 for (int i = 1; i < 1 << m; i++) { // 枚举 1 ~ 2^m - 1
        int t = 1, cnt = 0;
        for (int j = 0; j < m; j++) { 
            if ((i >> j & 1) > 0) { // 枚举为1的每一位
                /// 对为1的集合进行选取
            }
        }
    }