Part1.题型基本条件及思路

一般地说，当一个动作能导致两个结果（例如摁开关能打开灯或关闭灯），就称之为开关灯问题。
设计数学模型：容斥原理

Part2.专题疑难突破（有内味了）

两个思路：

1.有规律时寻找规律
2.无规律时进行模拟

通式：令i为按开关的次数,$0$为关着的灯，$1$为开着的灯
1. 若此灯初始状态为$0$，i%2==1时此灯被打开，i%2==0时此灯仍然关闭
2. 若此灯初始状态为$1$，i%2==1时此灯被关闭，i%2==0时此灯仍然为开

Part3.一些例子

eg1（寻找规律）:

题目描述

假设有 NN 盏灯（NN 为不大于 5000 的正整数），从 1 到 N 按顺序依次编号，初始时全部处于开启状态；第一个人（1 号）将灯全部关闭，第二个人（2 号）将编号为 2 的倍数的灯打开，第三个人（3 号）将编号为 3 的倍数的灯做相反处理（即，将打开的灯关闭，将关闭的灯打开）。依照编号递增顺序，以后的人都和 3 号一样，将凡是自己编号倍数的灯做相反处理。问当第 N 个人操作完之后，有哪些灯是关闭着的？

输入格式

输入为一行，一个整数 N，为灯的数量。

输出格式

输出为一行，按顺序输出关着的灯的编号。编号与编号之间间隔一个空格。

$\color{#0000FF}{思考过后，发现规律：}$
只有完全平方数的因数个数为奇数，其余数都是偶数，而按动偶数次下也就相当于没按了，所以最后还是亮的（因为一开始灯也都是亮的），那么最后关着的灯就是这些编号为$\color{#FF0000}{完全平方数}$的灯。
我们只需一个循环输出 1 到 n 之间的完全平方数，整个代码时间复杂度只有 $O(\sqrt{n})$

代码实现：

#include<iostream>
using namespace std;
int main(){
    int n;
    cin>>n;
    for(int i=1;i*i<=n;i++) 
    cout<<i*i<<" ";
    return 0;
}

eg1习题训练:

题目描书

首先所有的灯都是关的，编号为 1 的人走过来，把是 1 的倍数的灯全部打开，编号为 2 的人把是 2 的倍数的灯全部关上，编号为 3 的人又把是 3 的倍数的灯开的关上，关的开起来……直到第 N 个人为止。

给定 N，求 N 轮之后，还有哪几盏是开着的。

输入格式

一个数 N，表示灯的个数和操作的轮数。

输出格式

若干数，表示开着的电灯编号。

看过题目后，不难发现，这和$eg1$完全一样，读者$\overset{jian\ yi}{不妨}$思考过后再往下看

代码实现（这不和eg1一样么）：

#include<iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int i=1;i*i<=n;i++)
    cout<<i*i<<" ";
    return 0;
}

eg2（模拟）：

题目描述

有一个由按钮组成的矩阵，其中每行有 6 个按钮，共 5 行。每个按钮的位置上有一盏灯。当按下一个按钮后，该按钮以及周围位置(上边、下边、左边、右边)的灯都会改变一次。即，如果灯原来是点亮的，就会被熄灭；如果灯原来是熄灭的，则会被点亮。在矩阵角上的按钮改变 3 盏灯的状态；在矩阵边上的按钮改变 4 盏灯的状态；其他的按钮改变 5 盏灯的状态。

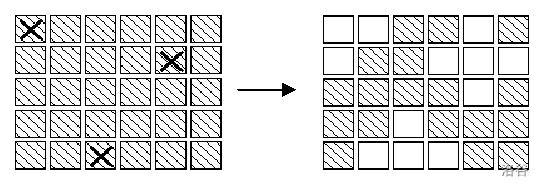
在上图中，左边矩阵中用 XX 标记的按钮表示被按下，右边的矩阵表示灯状态的改变。对矩阵中的每盏灯设置一个初始状态。请你按按钮，直至每一盏等都熄灭。与一盏灯毗邻的多个按钮被按下时，一个操作会抵消另一次操作的结果。在下图中，第 2 行第 3、5 列的按钮都被按下，因此第 2 行、第 4 列的灯的状态就不改变。

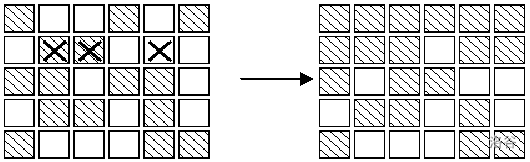
请你写一个程序，确定需要按下哪些按钮，恰好使得所有的灯都熄灭。根据上面的规则，我们知道 1)第 2 次按下同一个按钮时，将抵消第 1 次按下时所产生的结果。因此，每个按钮最多只需要按下一次；2)各个按钮被按下的顺序对最终的结果没有影响；3)对第 1 行中每盏点亮的灯，按下第 2 行对应的按钮，就可以熄灭第 1 行的全部灯。如此重复下去，可以熄灭第 1、2、3、4 行的全部灯。同样，按下第 1、2、3、4、5 列的按钮，可以熄灭前 5 列的灯。

输入格式

5 行组成，每一行包括 6 个数字（ 0 或 1 ）。相邻两个数字之间用单个空格隔开。0 表示灯的初始状态是熄灭的，1 表示灯的初始状态是点亮的。

输出格式

5 行组成，每一行包括 6 个数字（0 或 1）。相邻两个数字之间用单个空格隔开。其中的 1 表示需要把对应的按钮按下，0 则表示不需要按对应的按钮。

代码实现：

#include<memory>
#include<string>
#include<cstring>
#include<iostream>
using namespace std;

int GetBit(char c, int i) { //取c的第i位
    return ( c >> i ) & 1;
}

void SetBit(char & c, int i, int v) { //设置c的第i位设为v
    if ( v )  c |= ( 1 << i);
    else   c &= ~( 1 << i);
}

void Flip(char & c, int i) { //将c的第i位取反
    c ^= ( 1 << i);
}

void OutputResult(int t, char result[]) { //输出结果

    for ( int i = 0; i < 5; ++i ) {
        for ( int j = 0; j < 6; ++j ) {
            cout << GetBit(result[i], j);
            if ( j < 5 ) cout << " ";
        }
        cout << endl;
    }
}

int main() {

    char oriLights[5]; //最初灯矩阵，一个字节表示一盏灯
    char lights[5]; //不停变化的灯矩阵
    char result[5]; //结果开关矩阵
    char switchs; //某一行的开关状态
    int T;

    //cin >> T;//输入T表示有T组测试数据
    T = 1;

    for ( int t = 1; t <= T; ++ t) {
        memset(oriLights, 0, sizeof(oriLights));
        for ( int i = 0; i < 5; i ++ ) { //读入最初灯状态
            for ( int j = 0; j < 6; j ++ ) {
                int s;
                cin >> s;
                SetBit(oriLights[i], j, s);
            }
        }

        for ( int n = 0; n < 64; ++n ) { //遍历首行开关的64种操作

            memcpy(lights, oriLights, sizeof(oriLights)); 

            switchs = n; //先假定第0行的开关需要的操作方案
            for ( int i = 0; i < 5; ++i ) {

                result[i] = switchs; //保存第i行开关的操作方案

                for ( int j = 0; j < 6; ++j ) { //根据方案修改第i行的灯

                    if ( GetBit(switchs, j)) {

                        //switchs的第j个位等于1表示需要按下第i行第j个按钮，等于0表示不需要按下该按钮
                        if ( j > 0) Flip(lights[i], j - 1); //改左灯

                        Flip(lights[i], j); //改开关位置的灯

                        if ( j < 5 ) Flip(lights[i], j + 1); //改右灯

                    }
                }

                if ( i < 4 ) lights[i + 1] ^= switchs; //改下一行的灯

                switchs = lights[i]; //第i+1行开关的操作方案由第i行灯的状态决定
            }

            if ( lights[4] == 0 ) {

                OutputResult(t, result);
                break;

            }
        } 
    }
    return 0;
}

So that’s all~see you~