本笔记内容来源于算法基础课

组合数

$C_a^b$代表从$a$个不同的数中选取$b$个数所有可能的方案数($a \geq b$)

$C_a^b = \frac{a!}{b! (a-b)!} = \frac{a \times (a-1) \times \dots \times (a-b+1)}{1 \times 2\times \dots \times b}$

求所有可能的$C_a^b$

递推

使用范围：$10^5$次询问，$1 \leq b \leq a \leq 2000$，时间复杂度为$O(N^2) = (2000^2)$

$C_a^b = C_{a-1}^b + C_{a-1}^{b-1}$

$C_a^b$代表从$a$个数中选$b$个的方案数，而从中选定一个数$x$，它存在被包含$C_{a-1}^b$和不包含$C_{a-1}^{b}$两种情况

因此可以使用递推的方式进行求解

static int c[N][N]; // 所有可能的组合数
static void init() {
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (j == 0) c[i][j] = 1; // 边界规定
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % M; // 通常模一个较大的数
}

预处理阶乘

使用范围：$10^5$次询问，$1 \leq b \leq a \leq 10^5$，时间复杂度为$O(N\lg N) = (10^5\lg(10^5)$

预处理出阶乘的结果,采用逆元$\frac{a}{b} \bmod p = ab^{-1} \bmod p$，因为$b, p$互质

$f(i) = i! \bmod p, inf(p) = (i!)^{-1} \bmod p = 1^{-1} \times 2^{-1} \cdots \times i^{-1}$

$C_a^b = f(a) \times inf(b-a) \times inf(b)$

使用快速幂可以在$\lg(k)$的时间复杂度内完成

static int fact[N]; // 阶乘
static int infact[N]; // 阶乘的逆
static void init() {
    fact[0] = 1; infact[0] = 1; // 边界情况
    for (int i = 1; i < N; i++) {
        fact[i] = (int)((long) fact[i - 1] * i % M);
        infact[i] = (int)(long) infact[i - 1] * qmi(i, M - 2, M) % M;
    }
}
......
int res = (int)((long)fact[a] * infact[b] % M * infact[a - b] % M); // 注意中间取一次模防止溢出

卢卡斯定理

使用范围：$20$次询问，$1 \leq b \leq a \leq 10^{18}, 1 \leq p\leq 10^5$ ，时间复杂度为$O(log_p N p \lg p) = O(10^5 \times 20 \times 20)$

卢卡斯(Lucas)定理：

$C_a^b \equiv C_{a \bmod p}^{b \bmod p} C_{a/p}^{b/p} (\mod p)$

$a, b$使用$k$进制进行表示

$a = a_k p^k + a_{k-1} p^{k-1} + \cdots + a_0 p^0$

$b = b_k p^k + b_{k-1} p^{k-1} + \cdots + b_0 p^0$

$(1+x)^p = 1 + C_p^1 x + C_p^2 x^2 + \cdots + C_p^p x^p$

由于$p$是质数，因此只有分子包含$p$，所以$C_p^k \bmod p = 0$

因此有

$(1+x)^p \equiv 1 + x^p \mod p$

$(1+x)^a = (1+x)^{a_0} + ((1+x)^p)^{a_1} + \cdots ((1+x)^{p^k})^{a_k} \equiv (1+x)^{a_0} + (1+x^{p})^{a_1} + \cdots + (1+x^{p^k})^{a_k}$

将左右两边的系数进行对应

static int lucas(long a, long b, int p) {
    if (a < p && b < p) return C(a, b);
    else return (int)((long)C(a % p, b % p) * lucas(a / p, b / p) % p)
}

static int C(int a, int b, int p) {
    long res = 1;
    for (int i = 1, j = a; i <= b; i++, j--) { // 组合数展开式定义
        res = (long)res * j % p; // 分子
        res = (long)res * qmi(i, p - 2) % p; // 分母
    }
    return (int)res;
}

高精度

使用范围：要求直接输出结果，结果范围超过long

从定义出发，需要实现高精度乘法和除法，为了减少运算量，使用分解质因数

$C_a^b = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_k^{\alpha_k}$

因此只需要实现高精度乘法即可

若直接分解每个数的质因数，则时间复杂度为$O(n\sqrt n)$。可以直接枚举包含所有质因数的倍数。

对于$a! = 1 \times 2 \times 3 \cdots \times a$ 包含$p$质因子的个数，等于这些数当中包含一个$p$的个数加上包含两个$p$的个数......

$\lfloor \frac{a}{p} \rfloor + \lfloor \frac{a}{p^2} \rfloor + \cdots$

对于包含了$p^k$的数，会在$p, p^2, \cdots p^k$各统计一次，因此总共会统计$k$次

static int get(int n, int p) {
    int res = 0;
    while (n > 0) {
        res += n / p;
        n /= p;
    }
    return res;
}

卡特兰数

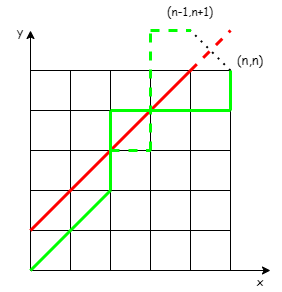
如图，考虑一个$n \times n$的方格，从$(0,0) \rightarrow (n,n)$中$x \ge y$的所有可能的路线数

对于任何在红线上方的路径都是违法的方案，如绿线所示。

• 而所有与红线相交的路线，都能以红线翻转映射到$(n-1,n)$的路线。
• 而所有到$(n-1,n)$的路线，都能够以第一个与红线相交的点翻转映射到$(n,n)$点

所以与红线相交到$(n,n)$的路线与所有到$(n-1,n+1)$的路线是一一对应的。

因此所有满足条件的路线$=$所有可能的路线$-$与红线相交的路线

$C_{2n}^n - C_{2n}^{n-1} = \frac{1}{n+1} C_{2n}^{n}$

$\frac{1}{n+1}C_{2n}^{n}$称为卡特兰数

不定方程

$x_1 + x_2 + \cdots + x_n = k, x_i \ge 1$，所有可能的方案数

采用隔板法，$\sum_k 1 = k$，从$k-1$个空位中插入$n - 1$个隔板，则能够分隔出$n$个数

因此所有的方案数为$C_{k - 1}^{n - 1}$

$x_1 + x_2 + \cdots + x_n = k, x_i \ge 0$，所有可能的方案数

等价于$(x_1 + 1) + (x_2 + 1) + \cdots + (x_n + 1) = k + n$

令$x_i’ = x_i + 1$

$x_1’ + x_2’ + \cdots + x_n’ = k + n, x_i’ \ge 1$，因此转化为第一种问题

所有的方案数为$C_{n+k-1}^{n-1} = C_{n+k-1}^{k}$