第7章 数学
1049. Counting Ones
笔记
- 可参考《算法基础课》数位统计DP的思路,这题只是那题的特例
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
const int N = 13; // 位数
int get(int l, int r, vector<int> num) {
int res = 0;
for (int i = l; i >= r; i--)
res = res * 10 + num[i];
return res;
}
int count (int n, int x) {
if (!n) return 0; // 特判
vector<int> num;
while(n) {
num.push_back(n % 10);
n /= 10;
}
n = num.size();
int res = 0;
for (int i = n - 1 - !x; i >= 0; i--) {
if (i < n - 1) {
// 左边存在
res += get(n - 1, i + 1, num) * pow(10, i);
if (!x) res -= pow(10, i); // 如果是计算0的位数,则不能让左边为全为0
}
if (x == num[i]) res += get(i - 1, 0, num) + 1;
else if (x < num[i]) res += pow(10, i);
}
return res;
}
int main() {
int n;
cin >> n;
cout << count(n, 1) << endl;
return 0;
}
1059. Prime Factors
笔记
- 当找到n的质因子a时,只需再从n/a找下一个质因子,这样可把时间复杂度降到O(√n)
- 注意
- 题目特判1的情况
- 写成
i <= n / i,防止乘法溢出 - 当循环结束后,n仍然可能是一个质因数,仍需要考虑
- 如果它是,则一定是最大的质因数且只有一个
- 如果不是,它一定是1
#include <iostream>
using namespace std;
string res;
void add(int x, int cnt) {
res += to_string(x);
if (cnt > 1) res += "^" + to_string(cnt);
res += "*";
}
int main() {
int n;
cin >> n;
if (n == 1) res = "1=1";
else {
res = to_string(n) + "=";
for (int i = 2; i <= n / i; i++)
if (n % i == 0) {
int cnt = 0;
while(n % i == 0) {
cnt++;
n /= i;
}
add(i, cnt);
}
if (n > 1) add(n, 1);
res.pop_back();
}
cout << res << endl;
return 0;
}
1081. Rational Sum
笔记
- 通分再计算,由于可能会产生乘法溢出,因此需要尽可能约分,即计算最大公约数后,分子和分母立即除以最大公约数
- 最大公约数可通过辗转相除法计算
- 假设t=gcd,则可以根据下式进行更深层的约分(否则过不了其中一个测试用例)
\frac{d \times a + b \times c}{b \times d}=\frac{ \frac{d}{t} \times a + \frac{b}{t} \times c}{ \frac{b}{t} \times d}
#include <iostream>
using namespace std;
typedef long long LL;
LL gcd(LL a, LL b) {
return b ? gcd(b, a % b) : a;
}
void f(LL& a, LL& b) {
// 约分
LL d = gcd(a, b);
a = a / d;
b = b / d;
}
int main() {
int n;
cin >> n;
LL a, b, as = 0, bs = 1;
while(n--) {
scanf("%lld/%lld", &a, &b);
f(a, b); // 约分
LL t = gcd(b, bs);
as = bs / t * a + b / t * as;
bs = b / t * bs;
f(as, bs); // 约分
}
if (as % bs == 0) printf("%lld\n", as / bs);
else if (as >= bs) printf("%lld %lld/%lld\n", as / bs, as % bs, bs);
else printf("%lld/%lld\n", as, bs);
return 0;
}
1088. Rational Arithmetic
笔记
- 根据通分公式计算即可,难点在于各种输出要求
#include <iostream>
using namespace std;
typedef long long LL;
LL gcd(LL a, LL b) {
return b ? gcd(b, a % b) : a;
}
void f(LL& a, LL& b) {
LL t = gcd(a, b);
a /= t;
b /= t;
}
string format(LL a, LL b) {
bool flag = (a < 0) ^ (b < 0);
a = abs(a);
b = abs(b);
string res;
if (a % b == 0) res = to_string(a / b);
else if (a > b) res = to_string(a / b) + ' ' + to_string(a % b) + '/' + to_string(b);
else res = to_string(a) + '/' + to_string(b);
if (flag) res = "(-" + res + ")";
return res;
}
string add(LL a, LL b, LL c, LL d, LL &p, LL& q) {
LL t = gcd(b, d);
p = b / t * c + d / t * a;
q = b / t * d;
f(p, q);
return format(p, q);
}
string sub(LL a, LL b, LL c, LL d, LL &p, LL& q) {
LL t = gcd(b, d);
p = d / t * a - b / t * c;
q = b / t * d;
f(p, q);
return format(p, q);
}
string mul(LL a, LL b, LL c, LL d, LL &p, LL& q) {
LL t = gcd(b, d);
p = a * c;
q = b * d;
f(p, q);
return format(p, q);
}
string div(LL a, LL b, LL c, LL d, LL &p, LL& q) {
if (b == 0 || c == 0) return "Inf";
LL t = gcd(b, d);
p = a * d;
q = b * c;
f(p, q);
return format(p, q);
}
void print(LL a, LL b, LL c, LL d) {
f(a, b); // 约分
f(c, d); // 约分
string x_str = format(a, b);
string y_str = format(c, d);
LL p, q; // 结果
cout << x_str + " + " + y_str + " = " + add(a, b, c, d, p, q) << endl;
cout << x_str + " - " + y_str + " = " + sub(a, b, c, d, p, q) << endl;
cout << x_str + " * " + y_str + " = " + mul(a, b, c, d, p, q) << endl;
cout << x_str + " / " + y_str + " = " + div(a, b, c, d, p, q) << endl;
}
int main() {
LL a, b, c, d;
scanf("%lld/%lld %lld/%lld", &a, &b, &c, &d);
print(a, b, c, d);
return 0;
}
1096. Consecutive Factors
笔记
- 穷举所有情况即可
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> res, num;
// 枚举所有质数
for (int i = 2; i <= n / i; i++)
if (n % i == 0) {
num.clear();
// 尝试以此为最小的因子构造
int m = n, j = i;
while(m % j == 0) {
num.push_back(j);
m /= j;
j++;
}
if (num.size() > res.size()) res = num;
}
if (res.empty()) res.push_back(n); // 自身是质数的情况
cout << res.size() << endl;
cout << res[0];
for (int i = 1; i < res.size(); i++) cout << '*' << res[i];
cout << endl;
return 0;
}
1103. Integer Factorization
当m=169,n=5,p=2时
| 物品i | 体积j | 重量k | 价值f |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 1 | 3 |
| … | … | … | … |
| 13 | 169 | 1 | 13 |
笔记
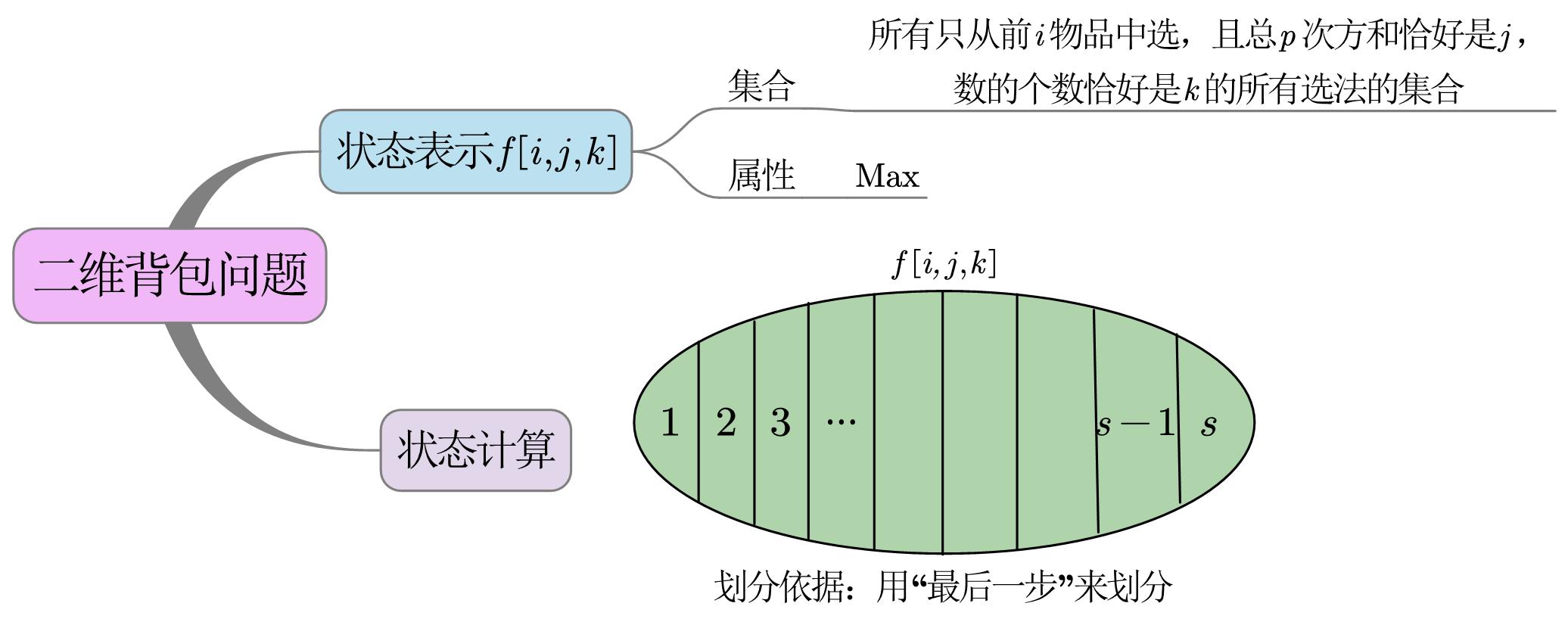
- 本题可看做是“二维完全背包具体方案”问题,可参考《算法提高课》“完全背包问题”、“二维费用的背包问题”和“背包问题求具体方案”
-
问题建模
- 假设t是要分解的整数,n是要分解的个数,p是幂,则可看做一种背包问题,记N=\lfloor m^{\frac{1}{p}} \rfloor
- 一共有N种物品a_1,a_2,\cdots, a_N
- 第i个物品a_i的体积v_i=i^p,重量m_i \equiv 1,价值w_i=i
- 背包的体积为t,最大承重量为n
- 问在背包的体积和重量达到最大值的条件下,怎么装物品才能让背包的价值最大?
- 假设t是要分解的整数,n是要分解的个数,p是幂,则可看做一种背包问题,记N=\lfloor m^{\frac{1}{p}} \rfloor
-
已有背包问题模型
- “完全背包问题”:可重复选择
- “二维费用的背包问题”:体积、重量、价值
- “背包问题求具体方案”:需要确定怎么选
f[i][j][k] == f[i-1][j][k]表示不选第i个物品f[i][j][k] == f[i][j-v][k-1]+i表示选第i个物品
-
算法实现细节
- 为了判断是否有解,需要把
f初始化为负数 - 最终解是
f[m][n][k]
- 为了判断是否有解,需要把
#define LOCAL
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
const int N = 410, M = 21;
int f[M][N][N]; // 考虑前i个物品,体积恰好为j,重量恰好为k的最大价值
int main() {
int m, n, p;
cin >> m >> n >> p;
memset(f, 0xef, sizeof f); // 初始化为负数
f[0][0][0] = 0; // 什么都不选时价值为0
// 动态规划
int i = 1;
int v = pow(i, p);
while(v <= m) {
// 构造第i个物品,直到第i个物品的体积超出背包所能容纳的体积
for (int j = 0; j <= m; j++) // 遍历背包最大体积的所有可能情况(目标)
for (int k = 0; k <= n; k++) { // 遍历背包最大重量的所有可能情况(个数)
f[i][j][k] = f[i - 1][j][k]; // 默认不选
if (j >= v && k >= 1)
f[i][j][k] = max(f[i][j][k], f[i][j - v][k - 1] + i); // 状态转移
}
i++; // 注意这个语句必须在计算v之前,否则不对
v = pow(i, p);
}
int max_i = i - 1; // 物品总数
// 输出结果
if (f[max_i][m][n] < 0) puts("Impossible"); // 无解
else {
printf("%d = ", m);
string res;
for (int i = max_i; i > 0; i--) {
int v = pow(i, p);
while (m >= v && n >= 1 && f[i][m][n] == f[i][m - v][n - 1] + i) {
res += to_string(i) + '^' + to_string(p) + " + ";
m -= v;
n--;
}
}
cout << res.substr(0, res.size() - 3) << endl;
}
return 0;
}
1104. Sum of Number Segments
笔记
-
对于第i个数,它在所有段求和中出现的次数为i \times (n - i + 1)
- 考虑含有a_1的项,显然其出现的次数为n
-
考虑含有a_2的项,可分为两部分,共出现2(n-1)次
- 有a_1且有a_2的项,出现次数为n-1
- 没有a_1但有a_2的项,出现次数也为n-1
-
考虑含有a_3的项,可分为三部分,同理共出现3(n-2)次
- 考虑含有a_i的项,猜测共出现i(n- i + 1)次
-
在计算时,先把
double类型的写在前边可防止计算乘法时溢出 - 不能用
g++编译,需要用更高级的clang++编译才能通过
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
long double res, a;
for (int i = 1; i <= n; i++) {
cin >> a;
res += a * i * (n - i + 1); // 先写double类型的防止乘法溢出
}
printf("%.2Lf\n", res);
return 0;
}
1112. Stucked Keyboard
笔记
-
一个字符有多种状态,可用
bool数组表示false表示该按键未使用过或有故障true表示该按键使用过且一定无故障(重复字符子串能被k整除)
-
首次遍历,用第一类双指针算法,找到重复字符子串,确定无故障的按键(子串长度不能被k整除,出现过未故障的情况,一定无故障)
- 再次遍历,输出有故障的按键以及正确的字符串。可用
bool数组记录已经输出的有故障按键,避免重复输出。
#include <iostream>
using namespace std;
const int N = 256; // ASCII码
bool keys[N], st[N];
int main() {
string s;
int k;
cin >> k >> s;
for (int i = 0; i < s.size(); i++) {
int j = i + 1;
while(j < s.size() && s[j] == s[i]) j++;
int len = j - i;
if (len % k) keys[s[i]] = true; // 出现过未故障的情况,一定无故障
i = j - 1;
}
string error_chars, res; // 有故障的按键,正确的输出
for (int i = 0; i < s.size(); i++) {
if (!keys[s[i]] && !st[s[i]]) {
error_chars += s[i]; // 有故障且未输出过
st[s[i]] = true;
}
res += s[i];
if (!keys[s[i]]) i += k - 1; // 按键有故障,跳过重复输出
}
cout << error_chars << endl << res << endl;
return 0;
}
1116. Come on! Let’s C
笔记
- 正整数集合可划分为\left\{1\right\}、\left\{ x \middle| x\,\,is\,\,prime \right\}和\left\{ x \middle| x\,\,is\,\,not\,\,prime \right\},分别对应三种奖项。
- 为了快速判断一个数是不是质数,考虑到ID范围有限,故可用筛素数算法找出给定范围内的全部素数,其方法是:从2开始遍历,把所有2的倍数标记为合数,即不是素数,然后再把下一个未被标记的数3,继续标记其倍数为合数,如此反复,把结果存储到布尔数组
isPrime[N]里。算法时间复杂度为O(n \log \log n) - 可用哈希表
rank存储每个编号的排名,例如rank[i] = j表示编号为i的选手,排名为j- 若
j > 0,表示选手存在 - 若
j == 0,表示选手不存在,输出Are you kidding? - 若
j == -1,表示选手已领取过奖品,输出Checked
- 若
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10010;
int ranks[N];
bool isPrime[N]; // true表示是素数,false表示是合数
void init(int n) {
memset(isPrime, true, sizeof isPrime);
for (int i = 2; i <= n; i++) {
if (isPrime[i]) {
for (int j = i * 2; j <= n; j += i)
isPrime[j] = false;
}
}
}
int main() {
int n, q, x;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &x);
ranks[x] = i;
}
init(n); // 筛素数
scanf("%d", &q);
while(q--) {
scanf("%d", &x);
printf("%04d: ", x);
if (!ranks[x]) puts("Are you kidding?");
else if (ranks[x] == -1) puts("Checked");
else {
int rank = ranks[x];
if (rank == 1) puts("Mystery Award");
else if (isPrime[rank]) puts("Minion");
else puts("Chocolate");
ranks[x] = -1;
}
}
return 0;
}
1152. Google Recruitment
笔记
- 整体思路是依次穷举,因此难点在怎么快速判断一个至多10^{9} - 1的数是不是素数。
- 可用试除法,至多需要试\sqrt{10^{9} - 1} \thickapprox 31622次,然而至多有10^4+10个子串需要判断,因此计算次数约为3.2 \times 10^8
- 为了优化时间复杂度,可用[2,31622]内的质数去试除,由费马定理知至多有\frac{n}{\ln n}=3051个质数,此时计算次数降为3.1 \times 10^7,而[2,10^3]内的质数可通过筛素数方法获取,计算次数近似于O(n \log \log n)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 40000;
bool isPrimes[N];
int primes[N], cnt;
void init() {
// 筛素数
memset(isPrimes, true, sizeof isPrimes);
cnt = 0;
for (int i = 2; i < N; i++) {
if (isPrimes[i]) {
primes[cnt++] = i; // 保存素数到primes数组中
for (int j = i * 2; j < N; j += i)
isPrimes[j] = false;
}
}
}
bool isPrime(int x) {
for (int i = 0; primes[i] <= x / primes[i]; i++)
if (x % primes[i] == 0)
return false;
return true;
}
int main() {
int n, k;
string s;
cin >> n >> k >> s;
init();
for (int i = 0; i + k - 1 < n; i++) {
string num = s.substr(i, k);
int x = stoi(num);
if (isPrime(x)) {
cout << num << endl;
return 0;
}
}
puts("404");
return 0;
}

