第6章 图
总结
最短路径主要用Dijkstra算法求解,题型如下:
- 求最短路径长度
- 求最短路径个数
- 求最短路径(
pre数组)
然后难度体现在,给图中结点赋权值,或者引入路径长度范围,或者引入各种约束,减少最短路径的选择,此类题常用解法有:
- 在Dijkstra算法中实现这些约束
- 记录所有最短路径,然后穷举符合题意的路径
其它注意事项:
- 当题目要计算最短路径个数时,不能让次要目标干扰其计算,而是以主要目标——路径最短——为主,因此在更新时,要确保
- 当
dist[t] + d[t][v] < dist[v]时,一定有cnt[v] = cnt[t] - 当
dist[t] + d[t][v] == dist[v]时,一定有cnt[v] += cnt[t],条件中一定不能包含次要目标。若题目需要考虑次要目标,则在执行后再处理次要目标
- 当
- 当题目要求具体最短路径时,尤其要求满足若干目标的最短路径时候,一定要让pre数组更新的位置位于满足全部目标的位置
- 如果不能嵌套在Dijkstra算法求解多目标最短路径,那么就穷举最短路径,然后再求最优解
if (最短路径<) {
更新最短路径长度
更新方案数
更新最短路径
更新约束1
更新约束2
} else if (最短路径==) {
更新方案数
if (次要目标1 <) {
更新最短路径
更新约束1
更新约束2
} else if (次要目标1 == && 次要目标2 <) {
更新最短路径
更新约束2
}
}
最短路径相关变量:
- 最短路径长度
dist[N](第一边权之和最短的路径的长度,唯一,假设第1边权为d[N][N],一定是求最小。初值为无穷大,结果在dist[dst]) - 最短路径个数
cnt[N](路径长度等于最短路径长度的路径个数,初值为0,cnt[src]=1) - 结点个数
num[N](满足所有约束的最短路径的结点个数,初值为0) - 最短路径
pre[N](最短路径中,当前结点的上一个结点,初值为0)
约束变量:
- 第二边权之和
sum_g[N](假设第2边权为g[N][N],可求最大或最小,不妨设最小,初值为0) - 点权之和
sum_w[N](假设点权为w[N],可求最大或最小,不妨设最小,初值为0)
根据上述定义,得到以下模板
// dijkstra初值
// dijkstra算法更新部分
if (dist[t] + d[t][v] < dist[v]) {
dist[v] = dist[t] + d[t][v];
cnt[v] = cnt[t];
num[v] = num[t] + 1;
pre[v] = t;
sum_g[v] = sum_g[t] + g[t][v];
sum_w[v] = sum_w[t] + w[v];
} else if (最短路径==) {
cnt[v] += cnt[t];
if (次要目标1 <) {
num[v] = num[t] + 1;
pre[v] = t;
sum_g[v] = sum_g[t] + g[t][v];
sum_w[v] = sum_w[t] + w[v];
} else if (次要目标1 == && 次要目标2 <) {
num[v] = num[t] + 1;
pre[v] = t;
sum_w[v] = sum_w[t] + w[v];
}
}
1003. Emergency
笔记
-
Dijkstra知识点
-
用途
- Dijkstra是最短路径算法,可求某个点到其它所有点的最小距离
-
适用范围
-
边权非负
-
有向图和无向图都可以(不一定是简单图,可以带有重边或自环)
-
-
思路
- 把起点到其它点的最短距离置为无穷大,起点到自身的最短距离置为0
- 选取最短距离最小的顶点u,并标记已选
- 用顶点u更新其它顶点的最小距离,dist(u)+d(u,v)<dist(v)时更新
- 直至所有点都选完
-
时间复杂度
-
朴素版O(n2+m)
-
堆优化O(mlogn)
-
-
-
本题思路
- 用Dijkstra算法计算起点到各个顶点的最短距离
- 当dist(u)+d(u,v)<dist(v)时,更新最短路径,顶点v方案数与选择的顶点u一致(因为没有增加最短路径),点权增加wv
- 当dist(u)+d(u,v)=dist(v)时,顶点v方案数应当加上顶点u的方案数(因为),点权更新为较大者
- 总结
- 最短路径:朴素Dijkstra(邻接矩阵)
- 求最短路径个数
- 求点权之和最大的最短路径
- 点权之和
- 特点
- 既有边权又有点权
- 边权之和最小,点权之和尽可能大
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, d[N][N]; // 邻接矩阵
int w[N]; // 点权
int src, dest; // 起点和终点
int dist[N]; // 最短距离
int cnt[N], sum[N]; // 方案数,最小点权数
bool st[N]; // 是否选过
void dijkstra() {
memset(dist, 0x7f, sizeof dist); // 初始化为无穷大
dist[src] = 0;
cnt[src] = 1;
sum[src] = w[src];
for (int u = 0; u < n; u++) {
// 选择一个最短路径最小的顶点
int t = -1;
for (int v = 0; v < n; v++)
if (!st[v] && (t == -1 || dist[v] < dist[t]))
t = v;
st[t] = true;
// 更新最短路径
for (int v = 0; v < n; v++)
if (dist[t] + d[t][v] < dist[v]) {
dist[v] = dist[t] + d[t][v];
cnt[v] = cnt[t]; // 方案数不变
sum[v] = sum[t] + w[v]; // 点权增加
} else if (dist[t] + d[t][v] == dist[v]) {
cnt[v] += cnt[t]; // 方案数增加
sum[v] = max(sum[v], sum[t] + w[v]); // 保存最大的点权
}
}
}
int main() {
int m;
cin >> n >> m >> src >> dest;
for (int i = 0; i < n; i++) cin >> w[i];
// 构建邻接矩阵
memset(d, 0x7f, sizeof d); // 初始化为无穷大
int u, v, c;
while(m--) {
cin >> u >> v >> c;
d[u][v] = min(d[u][v], c); // 处理自环和多重弧的情况
d[v][u] = d[u][v]; // 双向边
}
dijkstra();
cout << cnt[dest] << ' ' << sum[dest] << endl;
return 0;
}
1030. Travel Plan
笔记
- 题目给了两个同构的无向图,只是对应边的权重不一样。可以根据题目所求有针对性的保存边
- 如果当前边的长度>=新长度,则同时读入新长度和新花费
- 这保证两个点之间的长度和花费一定是同一对的,而不是两对的组合
- 在更新最短距离和最少花费时,可按如下策略更新
- 当新路径更短时,同时更新最短距离和最少花费(注意,此时可能“最少花费”会变更大,但依旧要更新)
- 当新路径和原来一样长,但花费更少时,只更新最少花费
- 题目要求输出路径,因此需要用一个变量保存最短路径的父节点,构造最终指向根节点的有向树,然后从目的结点往前输出到源节点即可
- 总结
- 多边权的存储
- 第一边权和第二边权是关联的,要变同时变
- 如果读入的第一边权较小,或第一边权相等但第二边权较小,则同时修改第一第二边权
- 最短路径:朴素Dijkstra(邻接矩阵)
- 求第二边权之和最小的最短路径
- 第一边权之和
- 具体路径
- 第二边权之和
- 求第二边权之和最小的最短路径
- 多边权的存储
- 特点
- 双边权(邻接矩阵存储)
- 第一边权之和最小,第二边权之和尽可能小
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, m, src, dest;
int d[N][N]; // 边权表示长度的无向图
int c[N][N]; // 边权表示花费的无向图
int min_d[N], min_c[N]; // 最短距离、最少花费
bool st[N]; // 已选结点
int pre[N]; // 保存最短路径指向的父节点(有向树)
void dijkstra() {
memset(min_d, 0x7f, sizeof min_d);
memset(min_c, 0x7f, sizeof min_c);
min_d[src] = min_c[src] = 0;
for (int u = 0; u < n; u++) {
// 选取最短距离最小的顶点
int t = -1;
for (int v = 0; v < n; v++) {
if (!st[v] && (t == -1 || min_d[v] < min_d[t])) {
t = v;
}
}
st[t] = true;
// 更新最短距离和最短路径
for (int v = 0; v < n; v++)
if (min_d[t] + d[t][v] < min_d[v]) {
min_d[v] = min_d[t] + d[t][v];
min_c[v] = min_c[t] + c[t][v];
pre[v] = t;
} else if (min_d[t] + d[t][v] == min_d[v] && min_c[t] + c[t][v] < min_c[v]) {
min_c[v] = min_c[t] + c[t][v];
pre[v] = t;
}
}
}
int main() {
cin >> n >> m >> src >> dest;
memset(d, 0x7f, sizeof d);
memset(c, 0x7f, sizeof c);
int u, v, distance, cost;
while(m--) {
cin >> u >> v >> distance >> cost;
if (distance <= d[u][v]) {
d[u][v] = d[v][u] = distance;
c[u][v] = c[v][u] = cost;
}
}
dijkstra();
string res;
for (int u = dest; u != src; u = pre[u])
res = to_string(u) + ' ' + res;
res = to_string(src) + ' ' + res;
res += to_string(min_d[dest]) + ' ' + to_string(min_c[dest]);
cout << res << endl;
return 0;
}
1034. Head of a Gang
笔记
- 由于结点用字符串
string表示,因此本题需要用哈希表unordered_map加快查找,邻接表,点权都用其实现- 在实现邻接表时,由于边是带有权重的,因此弧应当用
pair<string, int>表示,每个顶点的邻边用vector<pair<string, int>>表示,整个邻接表用unordered_map<vector<pair<string, int>>> - 点权用
unordered_map<string, int>表示
- 在实现邻接表时,由于边是带有权重的,因此弧应当用
- 题目要求找连通分量,但图中可能存在环,因此需要借助
unordered_map<string, bool>来辅助DFS记录结点的访问情况,从而能找到所有连通分量 - 总结
- 顶点个数不确定,而且顶点用字符串表示,难以用静态链表实现的邻接表,因此改用基于STL的邻接表
- 给出边权,但需要计算各个结点的点权(邻接边权之和)
- 找满足条件的连通分量:DFS
- 特点
- 边权转成点权
#include <iostream>
#include <unordered_map>
#include <algorithm>
#include <vector>
using namespace std;
unordered_map<string, vector<pair<string, int>>> g; // 邻接表
unordered_map<string, int> w; // 点权
unordered_map<string, bool> st; // 访问情况
int n, k;
int dfs(string u, vector<string>& nodes) {
st[u] = true;
nodes.push_back(u);
int sum = 0;
for(auto edge : g[u]) {
string v = edge.first;
sum += edge.second;
if (!st[v]) sum += dfs(v, nodes);
}
return sum;
}
int main() {
cin >> n >> k;
string u, v;
int l;
while(n--) {
cin >> u >> v >> l;
g[u].push_back({v, l});
g[v].push_back({u, l});
w[u] += l; // 更新点权
w[v] += l;
st[u] = false;
st[v] = false;
}
vector<pair<string, int>> res;
for (auto item : w) {
string u = item.first;
if (!st[u]) {
vector<string> nodes; // 当前连通分量的所有结点
int sum = dfs(u, nodes) / 2; // 连通分量的边权之和(包含重复计算)
if (nodes.size() > 2 && sum > k) {
string boss = "";
for (string node : nodes)
if (boss == "" || w[node] > w[boss])
boss = node;
res.push_back({boss, nodes.size()});
}
}
}
sort(res.begin(), res.end());
cout << res.size() << endl;
for (auto item : res)
cout << item.first << ' ' << item.second << endl;
return 0;
}
1087. All Roads Lead to Rome
笔记
- 本题是点权+边权的图,要求起点到终点的边权之和最小,如果存在多个则要求点权之和最大(注意不包括起点的点权),如果点权之和仍然相同,则选取平均点权最大的,即结点数少的最短路径
- 注意输入带有点权的顶点时,不含起点,因此之后只会给n-1个结点的权值,注意输入的处理
- 本题难点在于修改Dijkstra算法,如何实现多个目标的选择
- 总结
- 给定顶点个数,但顶点用字符串表示,只需用哈希表作为桥梁即可继续使用静态链表表示邻接表,同时还需要一个逆映射把序号转成城市名
- 最短路径:朴素Dijkstra(邻接矩阵)
- 求最短路径个数
- 求点权之和最大,结点个数最少的最短路径
- 边权之和
- 点权之和
- 结点个数
- 特点
- 既有边权又有点权
- 边权之和最小,点权之和尽可能大,结点个数尽可能小
- 相比1003题,本题结点用字符串表示
- 相比1034题,本题给了结点个数,可用哈希表存储结点名称与下标的关系,从而继续使用静态链表
#include <iostream>
#include <cstring>
#include <vector>
#include <unordered_map>
using namespace std;
const int N = 210;
const string DEST = "ROM"; // 终点
unordered_map<string, int> h; // 哈希表,映射城市名和顶点编号
string city[N];
int n, m, w[N], cost[N][N];
string start;
int min_cost[N], happy[N];
bool st[N];
int pre[N]; // 最短路径
int cnt[N]; // 方案数
int sum[N]; // 最短路径的结点个数
void dijkstra() {
memset(min_cost, 0x3f, sizeof min_cost);
min_cost[h[start]] = 0;
cnt[h[start]] = 1;
for (int u = 0; u < n; u++) {
int t = -1;
for (int v = 0; v < n; v++)
if (!st[v] && (t == -1 || min_cost[v] < min_cost[t]))
t = v;
st[t] = true;
for (int v = 0; v < n; v++)
if (min_cost[t] + cost[t][v] < min_cost[v]) {
min_cost[v] = min_cost[t] + cost[t][v]; // 代价
happy[v] = happy[t] + w[v]; // 幸福感
cnt[v] = cnt[t]; // 方案数
sum[v] = sum[t] + 1; // 路径结点数
pre[v] = t; // 所在最短路径的父节点
} else if (min_cost[t] + cost[t][v] == min_cost[v]) {
cnt[v] += cnt[t];
if (happy[t] + w[v] > happy[v]) {
happy[v] = happy[t] + w[v]; // 幸福感
sum[v] = sum[t] + 1; // 路径结点数
pre[v] = t; // 所在最短路径的父节点
} else if (happy[t] + w[v] == happy[v] && sum[t] + 1 < sum[v]) {
// 最短路径结点数越少,平均幸福感越大
sum[v] = sum[t] + 1; // 所在最短路径的父节点
pre[v] = t; // 所在最短路径的父节点
}
}
}
}
int main() {
cin >> n >> m >> start;
city[0] = start;
h[start] = 0;
int weight;
for (int u = 1; u < n; u++) {
cin >> city[u] >> w[u];
h[city[u]] = u;
}
memset(cost, 0x3f, sizeof cost);
string city_1, city_2;
while(m--) {
cin >> city_1 >> city_2 >> weight;
int u = h[city_1], v = h[city_2];
cost[u][v] = cost[v][u] = min(cost[u][v], weight);
}
dijkstra();
int dest = h[DEST]; // 目的城市所在的结点编号
cout << cnt[dest] << ' ' << min_cost[dest] << ' ' << happy[dest] << ' ' << happy[dest] / sum[dest] << endl;
int src = h[start];
string path;
for (int p = dest; p != src; p = pre[p])
path = "->" + city[p] + path;
path = start + path;
cout << path << endl;
return 0;
}
1111. Online Map
笔记
- 题目是有向图,可用邻接表存储
- 可用两个Dijkstra算法分别实现两个子问题的算法
- 最短路径:① 路径长度 ② 花费时间
- 最快路径:① 花费时间 ② 结点个数
- 总结
- 多边权的存储
- 不能用邻接矩阵存储,因为需要求两种目标不同的最短路径,它们依赖的边权不一样,因此本题必须用邻接表存储
- 最短路径:朴素Dijkstra(邻接表)
- 求第一边权之和最小,第二边权之和尽可能大的路径
- 第一边权之和
- 具体路径
- 求第二边权之和最小,结点数尽可能少的路径
- 第二边权之和
- 具体路径
- 求第一边权之和最小,第二边权之和尽可能大的路径
- 多边权的存储
- 特点
- 双边权(邻接表存储)
- 求第一边权之和最小,第二边权之和尽可能大的路径
- 求第二边权之和最小,结点数尽可能少的路径
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
const int N = 510, M = N * N;
int n, m;
int h[N], e[M], ne[M], d[M], c[M], idx;
int dist[N], cost[N], pre[N];
bool st[N];
int src, dest;
void add(int u, int v, int w_dist, int w_cost) {
e[idx] = v;
d[idx] = w_dist;
c[idx] = w_cost;
ne[idx] = h[u];
h[u] = idx++;
}
string get_path(int pre[]) {
vector<int> path;
for (int p = dest; p != src; p = pre[p])
path.push_back(p);
path.push_back(src);
reverse(path.begin(), path.end());
string res;
for (int elem : path)
res += to_string(elem) + " -> ";
return res.substr(0, res.size() - 4);
return res;
}
void init_dijkstra() {
memset(dist, 0x7f, sizeof dist);
memset(cost, 0x7f, sizeof cost);
memset(st, 0, sizeof st);
memset(pre, 0, sizeof pre);
dist[src] = 0;
cost[src] = 0;
}
pair<int, string> dijkstra_1() {
init_dijkstra();
for (int i = 0; i < n; i++) {
int u = -1;
for (int v = 0; v < n; v++)
if (!st[v] && (u == -1 || dist[v] < dist[u]))
u = v;
st[u] = true;
for (int p = h[u]; ~p; p = ne[p]) {
int v = e[p];
if (dist[u] + d[p] < dist[v]) {
dist[v] = dist[u] + d[p];
cost[v] = cost[u] + c[p];
pre[v] = u;
} else if (dist[u] + d[p] == dist[v] && cost[u] + c[p] < cost[v]) {
cost[v] = cost[u] + c[p];
pre[v] = u;
}
}
}
return {dist[dest], get_path(pre)};
}
pair<int, string> dijkstra_2() {
init_dijkstra();
for (int i = 0; i < n; i++) {
int u = -1;
for (int v = 0; v < n; v++)
if (!st[v] && (u == -1 || cost[v] < cost[u]))
u = v;
st[u] = true;
for (int p = h[u]; ~p; p = ne[p]) {
int v = e[p];
if (cost[u] + c[p] < cost[v]) {
cost[v] = cost[u] + c[p];
dist[v] = dist[u] + 1;
pre[v] = u;
} else if (cost[u] + c[p] == cost[v] && dist[u] + 1 < dist[v]) {
dist[v] = dist[u] + 1;
pre[v] = u;
}
}
}
return {cost[dest], get_path(pre)};
}
int main() {
scanf("%d%d", &n, &m);
int u, v, type, w_dist, w_cost;
memset(h, -1, sizeof h);
while(m--) {
scanf("%d%d%d%d%d", &u, &v, &type, &w_dist, &w_cost);
add(u, v, w_dist, w_cost);
if (!type) add(v, u, w_dist, w_cost);
}
scanf("%d%d", &src, &dest);
auto res_1 = dijkstra_1();
auto res_2 = dijkstra_2();
if (res_1.second == res_2.second)
printf("Distance = %d; Time = %d: %s\n", res_1.first, res_2.first, res_1.second.c_str());
else {
printf("Distance = %d: %s\n", res_1.first, res_1.second.c_str());
printf("Time = %d: %s\n", res_2.first, res_2.second.c_str());
}
return 0;
}
1122. Hamiltonian Cycle
笔记
- 哈密顿回路判定条件
- 起点和终点相同
- 每一步都有边
- 所有点均走到
- 恰好走了n+1个顶点
#include <iostream>
#include <cstring>
using namespace std;
const int N = 210;
int n, path[N * N];
bool g[N][N], st[N];
bool check(int m, int path[]) {
if (m != n + 1) return false; // 个数不是n+1
if (path[0] != path[m - 1]) return false; // 起点和终点不一致
memset(st, 0, sizeof st);
for (int i = 0; i < m - 1; i++) {
st[path[i]] = true;
if (!g[path[i]][path[i + 1]])
return false; // 不存在边
}
for (int i = 1; i <= n; i++)
if (!st[i]) return false; // 有顶点没遍历到
return true;
}
int main() {
int m, u, v;
scanf("%d%d", &n, &m);
while(m--) {
scanf("%d%d", &u, &v);
g[u][v] = g[v][u] = true;
}
int k;
scanf("%d", &k);
while(k--) {
scanf("%d", &m);
for (int i = 0; i < m; i++)
scanf("%d", &path[i]);
if (check(m, path)) puts("YES");
else puts("NO");
}
return 0;
}
1126. Eulerian Path
笔记
- 欧拉图
- 连通
- 所有点的度数为偶数(具有欧拉回路)
- 半欧拉图
- 连通
- 2个点的度数是奇数,其余是偶数(具有欧拉路径)
- 判断连通性可用DFS或并查集
#include <iostream>
using namespace std;
const int N = 510;
int n, m, d[N];
bool g[N][N], st[N];
int dfs(int u) {
st[u] = true;
int cnt = 1;
for (int v = 1; v <= n; v++)
if (!st[v] && g[u][v])
cnt += dfs(v);
return cnt;
}
int main() {
cin >> n >> m;
int u, v;
while(m--) {
cin >> u >> v;
g[u][v] = g[v][u] = true;
d[u]++;
d[v]++;
}
int cnt = dfs(1); // 顶点从1开始编号
cout << d[1];
for (int i = 2; i <= n; i++)
cout << ' ' << d[i];
cout << endl;
if (cnt != n) puts("Non-Eulerian"); // 不连通,一定是非欧拉图
else {
int odd_cnt = 0;
for (int i = 1; i <= n; i++)
if (d[i] % 2)
odd_cnt++;
if (odd_cnt == 0) puts("Eulerian"); // 欧拉图
else if (odd_cnt == 2) puts("Semi-Eulerian"); // 半欧拉图
else puts("Non-Eulerian"); // 非欧拉图
}
return 0;
}
1131. Subway Map
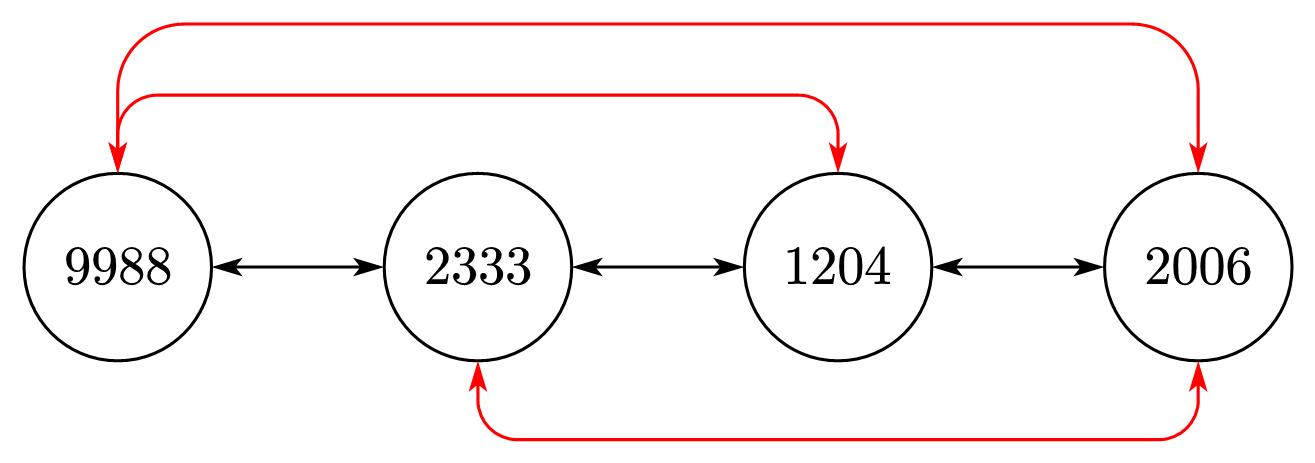
笔记
- 题目理论上至多有10000×10000=108种边,其中10000代表所有可能编号的结点个数(0000~9999),大约需要400MB>64MB的内存才能保存所有情况,超出空间限制,因此一定不能采用邻接矩阵保存网络结构。但数据范围限制至多有N×M2⩽条边,因此需要使用邻接表存储网络结构
- 由于不同边属于且仅属于某个地铁线路,因此还需要额外保存每条边属于哪条地铁线
- 在多个地铁线交汇的站点,需要额外处理。y总给出的一种方式是,对每条地铁线构造完全图,如上图所示,在题目给定的黑色双向边基础上,额外增加红色的双向边。
- 在某条地铁线上寻找u到v的最短路径时,能直接获得路径长度,此时的路径长度表示的不是两站直接的地理距离,而是二者的站点个数,同时在搜索时不必一步步走到该路径,用空间换时间
- 另一方面,在需要经过换乘地铁站时,才会出现中间结点,此时路径的结点数表示的是换乘地铁的次数
- 综上所述,距离
dist表示路过的站点数,中间结点个数cnt表示换乘地铁的次数 - 在实现Dijkstra算法时,优先考虑
dist最小,再考虑cnt最小
- 总结
- 存储
- 顶点数过多,只能用邻接表
- 算法
- 在存储边时,同时记录边所述的地铁线路为了优化查找效率,可把每一条地铁线路构造成完全图,新边长度按如下计算
- 如果地铁线路是直线型,则长度定义为两个站点间的站点数
- 如果地铁线路是环形,则长度定义为向左走和向右走的最小值
- 优化后,起点到终点路径的长度为站点总数,路径结点个数(不含首尾)为换乘次数
- 由于本题数据量比较大,因此用堆优化的Dijkstra算法
- 在存储边时,同时记录边所述的地铁线路为了优化查找效率,可把每一条地铁线路构造成完全图,新边长度按如下计算
- 存储
- 特点
- 虽然本题也是给字符串形式的结点,但依旧个数过多,不能用哈希表压缩
- 本题优化存储结构(构造完全图)后,算法效率得到了显著提升,而且更便于求解本问题
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int N = 10010, M = 1000010, K = 100;
typedef pair<int, int> PII;
int h[N], e[M], ne[M], d[M], line[M], idx;
int dist[N], cnt[N]; // 站点数,换乘地铁数
int path[K], pre[N];
bool st[N];
string info[N];
char info_line[50];
int n, m, k;
void add(int u, int v, int length, int id) {
e[idx] = v;
d[idx] = length;
line[idx] = id;
ne[idx] = h[u];
h[u] = idx++;
}
// 堆优化版Dijkstra算法,O(mlogn)时间复杂度
void dijkstra(int src, int dest) {
memset(dist, 0x3f, sizeof dist);
memset(cnt, 0x3f, sizeof cnt);
memset(st, 0, sizeof st);
priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
dist[src] = 0;
cnt[src] = 0;
heap.push({0, src}); // 放入最短距离和当前边的终点
while(heap.size()) {
PII item = heap.top();
heap.pop();
int u = item.second;
if (u == dest) break;
if (st[u]) continue;
st[u] = true;
for (int p = h[u]; ~p; p = ne[p]) {
int v = e[p];
if (dist[u] + d[p] < dist[v]) {
dist[v] = dist[u] + d[p];
cnt[v] = cnt[u] + 1;
pre[v] = u;
sprintf(info_line, "Take Line#%d from %04d to %04d.\n", line[p], u, v);
info[v] = info_line;
heap.push({dist[v], v});
} else if (dist[u] + d[p] == dist[v] && cnt[u] + 1 < cnt[v]) {
cnt[v] = cnt[u] + 1;
pre[v] = u;
sprintf(info_line, "Take Line#%d from %04d to %04d.\n", line[p], u, v);
info[v] = info_line;
}
}
}
cout << dist[dest] << endl;
string output;
for (int v = dest; v != src; v = pre[v])
output = info[v] + output;
cout << output;
}
int main() {
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i++) {
scanf("%d", &m);
for (int j = 0; j < m; j++)
scanf("%d", &path[j]);
// 转换成完全图
int length;
for (int j = 0; j < m; j++)
for (int k = j + 1; k < m; k++) {
if (path[0] != path[m - 1]) length = k - j;
else length = min(k - j, m - 1 - k + j);
add(path[j], path[k], length, i);
add(path[k], path[j], length, i);
}
}
int q, src, dest;
scanf("%d", &q);
while(q--) {
scanf("%d%d", &src, &dest);
dijkstra(src, dest);
}
return 0;
}
1134. Vertex Cover
笔记
- 按顶点覆盖的定义,模拟实现即可
- 可用
bool静态数组保存顶点子集,当存在一条边没被覆盖时,立即停止输出No,减少计算次数 - 总结
- 根据定义判断
- 如果存在一条边的两个顶点都不在顶点子集中,则不能顶点覆盖
- 哈希表加快查找
- 根据定义判断
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 10010, M = 10010;
typedef pair<int, int> PII;
bool st[N]; // 顶点子集
PII e[M]; // 边集
int n, m;
int main() {
cin >> n >> m; // 采用静态数组,这里的n没用
for (int i = 0; i < m; i++)
cin >> e[i].first >> e[i].second;
int q;
cin >> q;
while(q--) {
memset(st, 0, sizeof st);
cin >> n;
int u;
for (int i = 0; i < n; i++) {
cin >> u;
st[u] = true;
}
bool flag = true;
for (int i = 0; i < m; i++)
if (!st[e[i].first] && !st[e[i].second]) {
flag = false; // 有一条边没被覆盖
break; // 提前结束,减少计算次数
}
if (flag) puts("Yes");
else puts("No");
}
return 0;
}
1139. First Contact
笔记
- 顶点编号的可取值范围过大,需要用哈希表压缩范围
- 穷举所有可能的情况即可
- 总结
- 顶点取值范围过大,可考虑用哈希表压缩,即使用一个映射和一个逆映射维护二者关系,进而继续使用邻接矩阵。
- 本题的结点不是等价的,分男女,由于题目需要按性别分类,因此可用邻接矩阵记录人与人之间的关系,再用哈希集合分别存储所有男生和所有女生的ID
- 由于查找范围较少,可直接枚举
- 根据首尾两人确定中间两人的性别,进而确定枚举范围
- 如果首尾和中间两人能连成一条线,则符合要求
- 排序结果输出
- 特点
- 和1087题存储的方式类似,用哈希表映射
- 用哈希表映射时,要时刻谨记所用的是顶点名称还是顶点编号
#include <iostream>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 310;
int n; // 总人数
bool g[N][N]; // 邻接矩阵
unordered_map<string, int> h; // 哈希映射:人 → id
string name[N]; // 反向映射
int id;
vector<int> boys, girls;
char a_buffer[6], b_buffer[6];
int main() {
int m;
scanf("%d%d", &n, &m);
// 读入关系网络并压缩
while(m--) {
scanf("%s%s", a_buffer, b_buffer);
// 转成string类型
string a_str = a_buffer, b_str = b_buffer;
if (a_buffer[0] == '-') a_str = a_str.substr(1); // 去掉负号
if (b_buffer[0] == '-') b_str = b_str.substr(1); // 去掉负号
// 映射(哈希压缩)
if (h.count(a_str) == 0) {
h[a_str] = ++id; // 加入哈希表
name[id] = a_str;
}
if (h.count(b_str) == 0) {
h[b_str] = ++id; // 加入哈希表
name[id] = b_str;
}
int a = h[a_str], b = h[b_str]; // 获取分配的序号
g[a][b] = g[b][a] = true; // 添加双向边
// 更新男孩和女孩集合
if (a_buffer[0] == '-') girls.push_back(a); // 集合可能有重复元素
else boys.push_back(a);
if (b_buffer[0] == '-') girls.push_back(b);
else boys.push_back(b);
}
// 去重
sort(boys.begin(), boys.end());
boys.erase(unique(boys.begin(), boys.end()), boys.end());
sort(girls.begin(), girls.end());
girls.erase(unique(girls.begin(), girls.end()), girls.end());
// 穷举关系,找到中间者c和d
int q;
scanf("%d", &q);
while(q--) {
scanf("%s%s", a_buffer, b_buffer);
// 转成string类型
string a_str = a_buffer, b_str = b_buffer;
if (a_str[0] == '-') a_str = a_str.substr(1); // 去掉负号
if (b_str[0] == '-') b_str = b_str.substr(1); // 去掉负号
int a = h[a_str], b = h[b_str]; // 获取分配的序号
// 穷举两个中间者
vector<int> c_set, d_set; // 遍历的集合(a和c,b和d的性别相同)
if (a_buffer[0] == '-') c_set = girls;
else c_set = boys;
if (b_buffer[0] == '-') d_set = girls;
else d_set = boys;
vector<pair<string, string>> res;
for (int c : c_set)
for (int d : d_set)
if (c != a && c != b && d != a && d != b
&& g[a][c] && g[c][d] && g[d][b])
res.push_back({name[c], name[d]});
sort(res.begin(), res.end());
printf("%d\n", res.size());
for (auto item : res)
printf("%s %s\n", item.first.c_str(), item.second.c_str());
}
return 0;
}
1142. Maximal Clique
笔记
- 根据定义依次判断是否是团和最大团即可
- 总结
- 根据定义判断
- 是否是完全图(穷举)
- 再添加一个顶点是否还能构成完全图(穷举)
- 根据定义判断
#include <iostream>
#include <cstring>
using namespace std;
const int N = 210;
int n, m;
bool g[N][N], st[N];
int points[N];
bool check_clique(int points[], int k) {
for (int i = 0; i < k; i++)
for (int j = i + 1; j < k; j++)
if (!g[points[i]][points[j]])
return false; // 少了一条边
return true;
}
bool check_max_clique(int points[], int k) {
memset(st, 0 ,sizeof st);
for (int i = 0; i < k; i++)
st[points[i]] = true;
for (int u = 1; u <= n; u++)
if (!st[u]) {
bool flag = true;
for (int i = 0; i < k; i++)
if (!g[u][points[i]]) {
flag = false;
break; // 不能拓展成更大的团
}
if (flag) return false; // 能拓展成更大的团,说明不是最大团
}
return true; // 是最大团
}
int main() {
cin >> n >> m;
int u, v;
while(m--) {
cin >> u >> v;
g[u][v] = g[v][u] = true;
}
int q;
cin >> q;
while(q--) {
int k;
cin >> k;
for (int i = 0; i < k; i++)
cin >> points[i];
if (check_clique(points, k)) {
if (check_max_clique(points, k)) puts("Yes");
else puts("Not Maximal");
} else puts("Not a Clique");
}
return 0;
}
1146. Topological Order
笔记
- 判断一个顶点序列是否是拓扑序列,可检查所有边是否满足先后关系,因此可用一个数组保存每个顶点出现的次序。当所有有向边都在给定序列满足先后次序时,该序列是拓扑序列。
- 如果直接用数组的前n个位置存储顶点序列,则难以直接获取顶点的出现次序,故可考虑用哈希表做逆映射:元素→出现次序。由于本题的顶点个数不多,故可用数组直接实现映射
- 总结
- 只需存储边
- 检查所有边是否在序列中满足先后关系
- 用逆映射加快查找
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1010, M = 10010;
typedef pair<int, int> PII;
int n;
int h[N]; // 哈希表,映射:元素→出现次序
PII e[M];
int main() {
int m;
cin >> n >> m;
int u, v;
for (int i = 0; i < m; i++)
cin >> e[i].first >> e[i].second;
int q;
cin >> q;
vector<int> res;
for (int i = 0; i < q; i++) {
for (int j = 1; j <= n; j++) {
cin >> u;
h[u] = j;
}
bool flag = true;
for (int j = 0; j < m; j++)
if (h[e[j].first] > h[e[j].second]) {
flag = false; // 出现逆序
break;
}
if (!flag) res.push_back(i);
}
for (int i = 0; i < res.size(); i++) {
cout << res[i];
if (i < res.size() - 1) cout << ' ';
}
return 0;
}
1150. Travelling Salesman Problem
笔记
- 判断要点
- ① 是否是n+1个点
- ② 是否是回路
- ③ 是否走得通
- ④ 是否遍历所有点
- 满足②③④一定是TSP回路,如果还满足①,则是简单TSP回路
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 210, M = 310;;
int n, m, d[N][N], k, path[M];
bool st[N];
int main() {
cin >> n >> m;
memset(d, -1, sizeof d);
int u, v, dist;
for (int i = 0; i < m; i++) {
cin >> u >> v >> dist;
d[u][v] = d[v][u] = dist;
}
int q;
cin >> q;
int min_i = 0, min_dist = 2e9;
for (int i = 1; i <= q; i++) {
cin >> k;
for (int j = 0; j < k; j++)
cin >> path[j];
memset(st, 0, sizeof st);
bool success = true; // 是否遍历所有顶点
int sum = 0;
for (int j = 0; j < k - 1; j++) {
int u = path[j], v = path[j + 1];
if (d[u][v] == -1) {
sum = -1; // 路径不连通
success = false;
break;
} else {
sum += d[u][v];
st[v] = true;
}
}
for (int u = 1; u <= n; u++)
if (!st[u]) {
success = false;
break;
}
if (path[0] != path[k - 1]) success = false;
if (success) {
if (k == n + 1) printf("Path %d: %d (TS simple cycle)\n", i, sum);
else printf("Path %d: %d (TS cycle)\n", i, sum);
}else {
if (sum == -1) printf("Path %d: NA (Not a TS cycle)\n", i);
else printf("Path %d: %d (Not a TS cycle)\n", i, sum);
}
if (success && sum < min_dist) {
min_dist = sum;
min_i = i;
}
}
printf("Shortest Dist(%d) = %d\n", min_i, min_dist);
return 0;
}
1154. Vertex Coloring
笔记
- 用邻接表存储图结构
- 用哈希集合记录颜色种类
- 总结
- 结点个数太多,用邻接表存储
- 遍历整个邻接表,如果相邻结点颜色相同,则不合法
- 用集合找到颜色个数
#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;
const int N = 10086, M = 20048;
int n, m, color[N];
int h[N], e[M], ne[M], idx;
void add(int u, int v) {
e[idx] = v;
ne[idx] = h[u];
h[u] = idx++;
}
int main() {
cin >> n >> m;
int u, v;
memset(h, -1, sizeof h);
for (int i = 0; i < m; i++) {
cin >> u >> v;
add(u, v);
add(v, u);
}
int q;
cin >> q;
unordered_set<int> color_id;
while(q--) {
color_id.clear();
for (int u = 0; u < n; u++) {
cin >> color[u];
color_id.insert(color[u]);
}
bool flag = true;
for (int u = 0; u < n && flag; u++)
for (int p = h[u]; ~p; p = ne[p]) {
int v = e[p];
if (color[u] == color[v]) {
flag = false;
break;
}
}
if (flag) printf("%d-coloring\n", color_id.size());
else puts("No");
}
return 0;
}
1018. Public Bike Management
笔记
路径要求
- ① 距离尽可能短
- ② 最初带去的自行车数量越少越好
- ③ 最终带回的自行车数量越少越好
其中②和③不能在Dijkstra算法中满足,没法确定从哪一条路径比较好。
假设最大容量为10,在最短路径上存在三个邻接结点i-1、i和i+1,各自的自行车数分别为2,9,2。显然各自需要的自行车数为-3,4,-3,求和得-2,看起来只需要从PBMC发出2辆即可。但把则结果代入,发现2 + 2 < 5,无法满足要求,因此不能通过简单加和求出最优的发出数量,故本题采用Dijkstra+暴搜的方式求解
首先用Dijkstra算法求出所有的最短路径,确保满足条件①。然后在所有最短路径里搜索出满足条件②和条件③的路径作为答案。由于最短路径不会太多,采用Dijkstra算法相当于“修枝”,减少搜索范围,因此这个算法是可行的。
为了记录Dijkstra算法的最短路径,可用vector<int> pre[N]保存最短路径的前驱结点。例如pre[u]表示结点u在所有最短路径可能的前驱结点,它是个变长数组vector<int>。在求最短路径时,从起点0出发。
在穷举时,由于记录的是前驱结点,因此需要反向遍历,即从终点S_p开始走到起点0。在遍历时,需要记录最初带去的自行车数量need,以及最终带回的自行车数量remain,二者的计算思路如下:
若结点i的权值w_i > \lceil \frac{C_{max}}{2} \rceil,则从结点i上取出w_i - \lceil \frac{C_{max}}{2} \rceil作为备选,计入remain变量中。若w_i < \lceil \frac{C_{max}}{2} \rceil,则先从remain中取出补给,此时分两类情况:
remain足够补给结点i,则让ramain减去补给的数量remain不足够补给结点i,先把ramain拿去全部补给,还差的部分计入need中,即需要从PBMC带去的自行车数量
为了方便,可在存储点权w_i时,让所有点权都- \lceil \frac{C_{max}}{2} \rceil,这样,只需根据点权正负判断。
总结
- 题目需要满足三个条件
- 路径是最短路径
- 带去的自行车数量最小
- 带回的自行车数量最大
- 穷举最短路径,依次判断是否满足符合条件
- 多条最短路径存储:
vector<int> pre[N]
特点
- 本题虽然输入的顶点数为n,但隐藏了起点0,因此所有结点编号为0~n,共n+1个结点,在实现Dijkstra算法时需要注意
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int max_size, n, v_end, m;
int w[N], d[N][N];
int dist[N];
bool st[N];
vector<int> pre[N];
int min_need = INF, min_remain = INF; // 最初带走,最终带回的自行车数量
vector<int> path, ans;
void dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[0] = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int u = 0; u <= n; u++)
if (!st[u] && (t == -1 || dist[u] < dist[t]))
t = u;
st[t] = true;
for (int u = 0; u <= n; u++)
if (dist[t] + d[t][u] < dist[u]) {
dist[u] = dist[t] + d[t][u];
pre[u].clear();
pre[u].push_back(t);
} else if (dist[t] + d[t][u] == dist[u])
pre[u].push_back(t);
}
}
void dfs(int u) {
// 反向遍历到起点
if (!u) {
// 已经走到起点
path.push_back(u);
// 正向走到终点,计算remain和need
int remain = 0, need = 0;
for (int i = path.size() - 1; i >= 0; i--) {
int v = path[i];
if (w[v] > 0) remain += w[v]; // 拿走多余的自行车
else {
// 需要补给自行车
if (remain >= abs(w[v])) remain -= abs(w[v]); // 从路上拿到的自行车补给
else {
// 从PBMC补给
need += abs(w[v]) - remain;
remain = 0;
}
}
}
if (need < min_need) {
// 优先选择最初带去自行车数量较少的路径
min_need = need;
min_remain = remain;
ans = path;
} else if (need == min_need && remain < min_remain) {
// 选择最终带回自行车数量较少的路径
min_remain = remain;
ans = path;
}
path.pop_back();
return;
}
path.push_back(u);
for (int v : pre[u]) dfs(v);
path.pop_back();
}
int main() {
cin >> max_size >> n >> v_end >> m;
// int half_size = (max_size + 1) / 2; // 上取整
int half_size = max_size / 2; // 上取整
for (int i = 1; i <= n; i++) {
cin >> w[i];
w[i] -= half_size;
}
memset(d, 0x3f, sizeof d);
int a, b, c;
while(m--) {
cin >> a >> b >> c;
d[a][b] = d[b][a] = min(d[a][b], c);
}
dijkstra();
dfs(v_end);
reverse(ans.begin(), ans.end());
cout << min_need << " ";
for (int u : ans)
if (u == 0) cout << u;
else cout << "->" << u;
cout << " " << min_remain;
return 0;
}
1072. Gas Station
笔记
- 加油站需要满足的条件
- ① 所有居民房都在范围内dist_i \leqslant D_s
- ② 最小的dist_i最大
- ③ dist的平均数最小(等价于总和最小)
- ④ 编号较小
- 从小到大枚举所有加油站的位置,这样就确保满足了最后一个条件④
- 由于加油站的编号是字符串,可以考虑把它编排到n+1~n+m中
- 为了判断条件①,可对每个加油站位置做一次Dijkstra算法,然后检查是否满足条件①
- 如果有多个满足,则再按②筛选;同理再按③筛选
- 注意,尽管不需要所有加油站都在被选加油站的范围内,但在求最短路径时,可通过加油站到达别的居民房,因此在编写Dijkstra算法时,核心部分需要考虑加油站
- 由于浮点数存储存在误差,在计算时会出现问题,下边给出保留一位小数的方法
- 补精度
(double) x + 1e-8 - 借助
round(),round(x * 10) / 10
- 补精度
- 特点
- 本题需要理清题意,加油站和居民楼都是结点,在调用Dijkstra算法时加油站结点需要视为普通结点,但在计算约束时,只要求居民楼的最短路径满足约束条件
- 浮点数精度问题+1e-8
- 在Dijkstra算法中,
min_d按最小值计算,此时初值应为INF;在main函数中,要求最大的best_min_d,此时初值应为-1。
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 1020, INF = 0x3f3f3f3f;
int n, m, k, d_max;
int d[N][N];
int d_min, d_sum;
int dist[N];
bool st[N];
int get(string s) {
// 把加油站位置映射到n+1 ~ n+m中
if (s[0] == 'G') return n + stoi(s.substr(1));
return stoi(s);
}
bool dijkstra(int u) {
memset(dist, 0x3f, sizeof dist);
memset(st, 0, sizeof st);
dist[u] = 0;
for (int i = 0; i < n + m - 1; i++) {
int t = -1;
for (int u = 1; u <= n + m; u++)
if (!st[u] && (t == -1 || dist[u] < dist[t]))
t = u;
st[t] = true;
for (int u = 1; u <= n + m; u++)
dist[u] = min(dist[t] + d[t][u], dist[u]);
}
d_min = INF, d_sum = 0;
for (int u = 1; u <= n; u++) {
if (dist[u] > d_max) return false;
else {
d_min = min(d_min, dist[u]);
d_sum += dist[u];
}
}
return true;
}
int main() {
memset(d, 0x3f, sizeof d);
cin >> n >> m >> k >> d_max;
string s1, s2;
int a, b, c;
for (int i = 0; i < k; i++) {
cin >> s1 >> s2 >> c;
a = get(s1);
b = get(s2);
d[a][b] = d[b][a] = min(d[a][b], c);
}
int best_pos = -1, best_d_min = 0, best_d_sum = INF;
for (int u = n + 1; u <= n + m; u++) {
if (dijkstra(u)) {
if (d_min > best_d_min) {
best_pos = u;
best_d_min = d_min;
best_d_sum = d_sum;
} else if (d_min == best_d_min && d_sum < best_d_sum) {
best_pos = u;
best_d_sum = d_sum;
}
}
}
if (best_pos == -1) puts("No Solution");
else {
printf("G%d\n", best_pos - n);
double average = round((double)best_d_sum * 10 / n) / 10; // 保留一位小数
printf("%.1lf %.1lf\n", (double)best_d_min, average);
}
return 0;
}
1076. Forwards on Weibo
笔记
- 用BFS找前L层(实际上是找前L+1层,然后去掉自身)
- 用于顶点数较多,考虑用邻接表存储。注意a关注了b,则b是a的粉丝,应当添加从b指向a的有向边,不能弄反
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 1010, M = 100010;
int h[N], e[M], ne[M], idx;
int n, m;
bool st[N];
void add(int u, int v) {
e[idx] = v;
ne[idx] = h[u];
h[u] = idx++;
}
int bfs(int start) {
queue<int> q;
memset(st, 0, sizeof st);
q.push(start);
st[start] = true;
int res = 0;
// 计算第2~L层结点数,第L+1层之后再算
for (int i = 0; i < m; i++) {
int len = q.size();
res += len;
for (int j = 0; j < len; j++) {
// 当前层有len个,因此只弹出len个
int u = q.front();
q.pop();
// 在队列中加入下一层结点
for (int p = h[u]; ~p; p = ne[p]) {
int v = e[p];
if (!st[v]) {
q.push(v);
st[v] = true;
}
}
}
}
return res + q.size() - 1; // 补上第L+1层结点,并去掉自身
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for (int u = 1; u <= n; u++) {
int t, v;
scanf("%d", &t);
while(t--) {
scanf("%d", &v);
add(v, u);
}
}
int k, u;
scanf("%d", &k);
while(k--) {
scanf("%d", &u);
printf("%d\n", bfs(u));
}
return 0;
}

