离散化详解及应用

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

离散化详解及应用

作者：

弑 , 2021-11-10 17:25:14 , 所有人可见 , 阅读 341

6

3

前言

离散化概念简单，但在具体落实过程发现，初学时实现细节上还有点小问题，且网上大都是很抽象化的理解总结，没有具体代码实例辅以讲解。所以，在这里还是记录一下自己的一些心得。

概述

离散化是程序设计中一个常用的技巧，它可以有效的降低时间复杂度。其基本思想就是在众多可能的情况中，只考虑需要用的值。离散化可以改进一个低效的算法，甚至实现根本不可能实现的算法。要掌握这个思想，必须从大量的题目中理解此方法的特点。例如，在建造线段树空间不够的情况下，可以考虑离散化。

上面是在网上找到我觉得比较好的一种关于离散化的解释。

但如果只看这段文字的话，对于离散化的概念理解上还是有点抽象。现在，让我们来看一道具体实例来体会一下：

什么是离散化？
应该如何离散化？
离散化后的数据应该如何使用？

例题

原题链接

假定有一个无限长的数轴，数轴上每个坐标上的数都是 $0$。

现在，我们首先进行 $n$ 次操作，每次操作将某一位置 $x$ 上的数加 $c$。

接下来，进行 $m$ 次询问，每个询问包含两个整数 $l$ 和 $r$，你需要求出在区间 [$l,r$] 之间的所有数的和。

输入格式

第一行包含两个整数 $n$ 和 $m$ 。

接下来 $n$ 行，每行包含两个整数 $x$ 和 $c$。

再接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$。

输出格式

共 $m$ 行，每行输出一个询问中所求的区间内数字和。

数据范围

$−10^9≤x≤10^9$
$1≤n,m≤10^5$
$−10^9≤ l ≤ r ≤10^9$
$−10000≤c≤10000$

输入样例：

输出样例：

8
0
5

问题分析

看到执行n次在某位置x上的加上c，并且还询问m次给定区间的和这种问题。第一反应就是这是道考察前缀和的题目。

但仔细看下数据范围： $−10^9≤x≤10^9$。。。。。。好家伙，姑且不说我们是否能开那么大的数组，就算开得了，那么大的范围做前缀和，预处理时O(n)的时间复杂度也是无法忍受的。

而再看一下我们实际需要处理的数据量 $n,m$ ，都是$10^5$ 量级相对 $10^9$ 来说很小，我们只需要聚焦处理这 $10^5$ 量级的数据即可。在这种情况下，我们就可以用离散化了。

下面用样例数据演示具体过程：

离散化_1

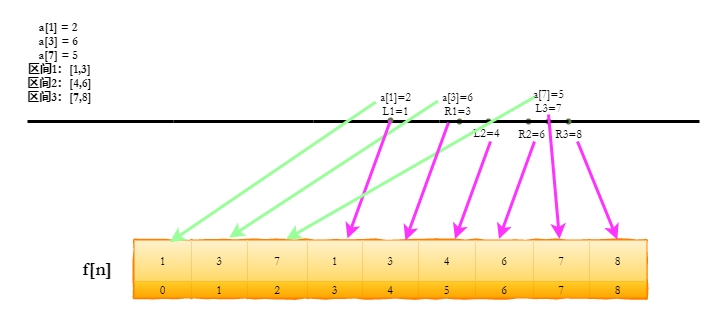
首先可以明确的是，在这题中我们离散化的对象是数轴的坐标。所以对于输入的位置x和对应的数值c，只需要把数轴下标放到数组 $f[n]$ 中即可，这里的 $f[n]$ 为离散化后的重映射数组。

注意，上图中的数组a不是真实的数组，只是为了方便演示写成了数组的形式，实现时，可以用结构体之类的方法创建一个二元组用于存储坐标x和对应的数值c。

同理，按输入顺序向 $f[n]$ 插入所有出现过的数轴坐标，形成上图中的 $f[n]$数组，图中出现 Lx、Rx，表示第x个区间的左边界和右边界。

到这里，离散化的第一步我们就完成了。

可以看到这个离散化后的新数组，有多个相同且无序的值，这肯定是不行的。所以第二步就是对 $f[n]$ 排序、去重，形成如下图的序列。

离散化2

ok，现在所有离散点对“紧挨”在一起了。但这个“紧挨”在一起的数组只是下标，不是实际的值。所以还要创建一个大小跟离散化后的数组 $f[n]$ 一样大的数组 $S[n]$ 用来存放未离散化前的下标值。

离散化3.

最后，第三步我们可以通过一个find函数，找出原下标经过离散化后的新坐标，并赋值即可。（find函数用二分查找实现即可）

过程如下图：

离散化4

至此，离散化处理就完成了。后面就是把离散化后的新数组当成普通数组一样进行前缀和处理即可。

代码

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef pair<int,int> PII;
const int N = 300010;
vector<PII> a,query;
vector<int> f;
int s[N];


int find(int x){
    return lower_bound(f.begin(),f.end(),x) - f.begin();
}

int main (){
    int n,m;
    cin>>n>>m;

    //第一步：把待离散化下标放入新数组
    for(int i=0;i<n;i++){
        int x,c;
        cin>>x>>c;
        //对 位置x 离散化
        f.push_back(x);
        a.push_back({x,c});
    }
    for(int i=0;i<m;i++){
        int l,r;
        //对 位置l,r 离散化
        cin>>l>>r;
        query.push_back({l,r});
        f.push_back(l);
        f.push_back(r);
    }

    //第二步：排序、去重
    f.push_back(-2e9);
    sort(f.begin(),f.end());
    f.erase(unique(f.begin(),f.end()),f.end());//去重

    //第三步：数值数组赋值
    for(int i=0;i<n;i++)s[find(a[i].first)]+=a[i].second;
    n = f.size();

    //普通前缀和处理
    for(int i = 1;i<n;i++)s[i]+=s[i-1];
    for(int i=0;i<m;i++){
        cout<< s[find(query[i].second)] - s[find(query[i].first)-1]<<endl;
    }
    return 0;
}