第9讲 查找

查找的基本概念

(1) 平均查找长度 ASL = 每个元素 查找概率 * 找到第i个元素需要进行的比较次数 的和。
ASL（成功） = 所有元素对应的概率 * 比较的次数 之和。

ASL（失败） = 所有区间的概率 * 比较的次数 之和。
PS：成功的情况只需要跟已有的元素进行比较，而失败的情况则需要跟所有位置相比较，即一些空位置上面
也算一次（即y总所讲的区间）。

(2) 决策树(判定树)
根据每一次的会出现判定的情况而产生的分支。

查找方式

顺序查找法

(1) 一般线性表的顺序查找
    a. 若每个元素查找概率相同，则 ASL(成功) = (1 + 2 + ... + n) / n = (n + 1) / 2
    b. ASL(失败) = n或n+1，取决于代码写法。
(2) 有序表的顺序查找
    a. 若每个元素查找概率相同，则 ASL(成功) = (1 + 2 + ... + n) / n = (n + 1) / 2
    b. ASL(失败) = (1 + 2 + ... + n + n) / (n + 1) = n / 2 + n / (n + 1)

折半查找法

保证序列有序才可以。

(1) ASL = log(n + 1) - 1

分块查找法

设共n个元素，每块s个元素，共b = n / s块。块内无序，块间有序。先判断在哪一个块内，再去块内判断。
(1) 顺序查找确定块：ASL(成功) = (s^2 + 2s + n) / (2s)，s = sqrt(n)时取最小值
(2) 二分查找确定块：log(n/s + 1) + (s - 1)/2

B树及其基本操作、B+树及其基本概念

(1) B树：应用在硬盘、文件系统、数据库方面
    [1] m阶B树，每个节点最多有m个孩子。
    [2] 每个节点最多有m-1个关键字（可以存有的键值对）。
    [3] 根节点最少可以只有1个关键字。
    [4] 非根节点至少有m/2个关键字。（一般是向下取整）
    [5] 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树
    中的所有关键字都大于它。
    [6] 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同。
    [7] 每个节点都存有索引和数据，也就是对应的key和value。
    [8] 所以，根节点的关键字数量范围：1 <= k <= m-1，非根节点的关键字数量范围：m/2 <= k <= m-1。

    插入和删除:
    1.插入时没有超过最大关键字个数就一直按照规则插入就行，当超过个数时，从中间的关键字进行分裂左右两边，
    中间的移到父结点。
    2.（建议模拟方便记忆）删除的时候，若是叶结点直接删除，删除完要看一下结点内的关键字个数符不符合对应的
    m阶B树结点内的关键字个数范围，若满足无需操作，若不足则看一下左右兄弟是不是有多的关键字个数（大于m/2）
    ，有就借（借的那个关键字上移到父结点替换掉对应的父关键字，父关键字下移到删除关键字的那个结点内）一个
    过来进行补充，若左右兄弟结点正好满足范围不多，则选择一个兄弟结点进行两个结点的合并。
    当删除的不是叶结点的时候，我们把它的后继覆盖给删除的关键字，删除后继。
    （以上个人理解，若读者不太明确还是建议多搜一些博客看一下。下面有y总上课用到的参考博客）



(2) B+树
    [1] B+跟B树不同B+树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得B+树每个非叶子节点所能
    保存的关键字大大增加；
    [2] B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次
    数据查询的次数都一样；
    [3] B+树叶子节点的关键字从小到大有序排列，左边结尾数据都会保存右边节点开始数据的指针。


(3) 参考链接：https://blog.csdn.net/Fmuma/article/details/80287924

    插入和删除：
    1.插入关键字过多的时候，同样需要分裂，不同的是若是叶结点的分裂，关键字上移的时候是复制一个上去成为索
    引，叶结点那个还会保留成真正的信息；当不是叶结点的时候，分裂上去就直接上去就行，原来结点处不需要在保
    留一份一样的，因为他是一个索引的信息不是数据信息。
    2.删除的时候，结点内关键字个数够不用管，当不够的时候兄弟够问兄弟结点借一个，同时记得更新父结点的索引
    信息，这个要注意；当兄弟结点也不够的时候，两个结点进行合并，合并完也要记得更新父结点内的索引信息



区别：
B树内部节点存储信息，B+树只有叶结点才存储信息（最底层的叶结点可以顺序遍历）

考题：

2011-42、2012-9、2013-10、2013-42、2014-9、2015-7、2016-9、2016-10、2017-8、2017-9、2018-8、2020-10

总结：

1. m阶B树结点内关键字个数范围：m/2上取整 -1 到 m - 1
   （根结点较特殊，最少有一个即可）

2. 顺序表里面存储的元素不一定数字，还有可能是字符串，若是字符串的话，就按照字典序来比（a-z）

3. 折半查找不说明的话，一般是采取向下取整。

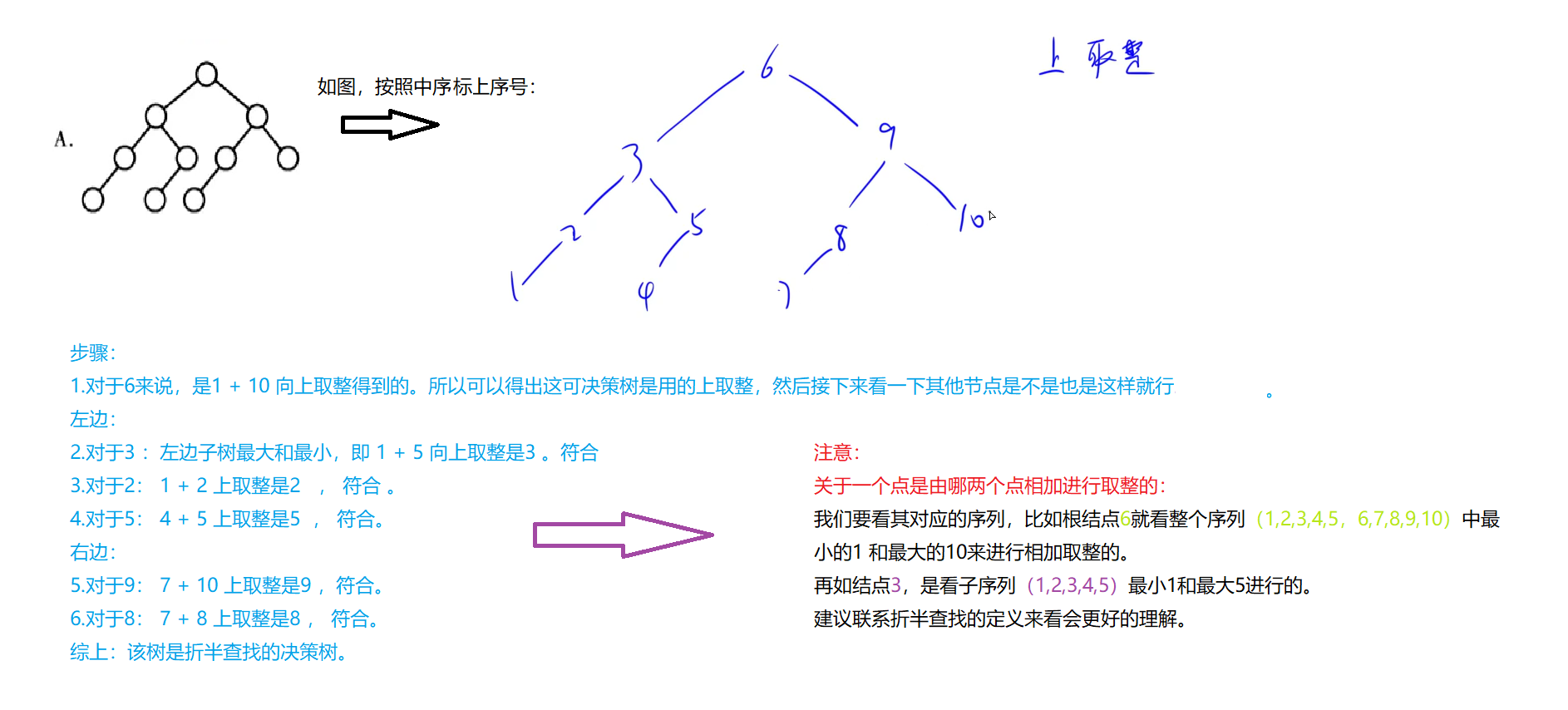
4. 能构成折半查找的序列，它的决策树中序序列是有序的，通过这个来判断。

（2017-8：判定二叉树是不是折半查找的决策树：先按照中序遍历依次标上编号，计算的时候看一下所有结点的下取整（有的是上取整，需要通过一次运算判断，然后在看其余结点）是不是一致的，若是则是，反之不是。）