算法提高课汇总

背包问题

可以认为是组合问题: 不考虑选择物品之间的关系, 只考虑选择物品的集合. 下面简单总结3个背包问题:
01背包; 完全背包; 多重背包. 利用Y式DP分析, 三种问题的状态表示相同, 不同点在于状态计算/
集合划分: 第$i$个背包可能选择个数的范围.

01背包

状态表示 dp[i,j]

• 集合: 从前$i$个物品中选择且总体积不超过$j$的所有选法.

• 属性: Max(物品价值最大)

状态计算

按第$i$个物品的选择个数划分, 对于第$i$个物品可以选择$[0, 1]$个(问题名称的来源). 从集合的定义出发,
考虑第$i$个物品选择$0$个和选择$1$个的情况:

• 第$i$个物品选择$0$个(不选): 问题等价于从前$i-1$个物品中选择且总体积不超过$j$的所有选法, 根据
  定义, 问题集合的最大值为: $dp[i-1,j]$

• 第$i$个物品选择$1$个: 已经确定了第$i$个物品的选择,此时问题剩余不确定部分等价于从前$i-1$个物品
  中选择且总体积不超过$j-v_i$的所有选法, 其中$v_i$对应第$i$的物品的体积, 不确定部分对应的集合的
  最大值为: $dp[i-1, j-v_i]$, 最后加上已经选择的第$i$个物品的价值$w_i$.

注意: 对于第二种情况可能由于体积限制无法选择第$i$个物品, 此时对应集合为$\varnothing$, 数值为$0$.

为保证每次计算的集合属性均为Max, 对于$dp[i, j]$, 其值为上述两个子集的最大值即可. 根据定义最终
问题转换为求解$dp[n][m]$.

代码实现

首先是根据上述分析得到的朴素版本.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 1010;

int n, m;
int v[N], w[N];
int dp[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 0; j <= m; j ++ )
        {
            dp[i][j] = dp[i - 1][j];
            if( j >= v[i] )
            {//存在第二种情况
                dp[i][j] = max( dp[i][j], dp[i - 1][j - v[i]] + w[i] );
            }
        }
    }
    cout << dp[n][m] << endl;

    return 0;
}

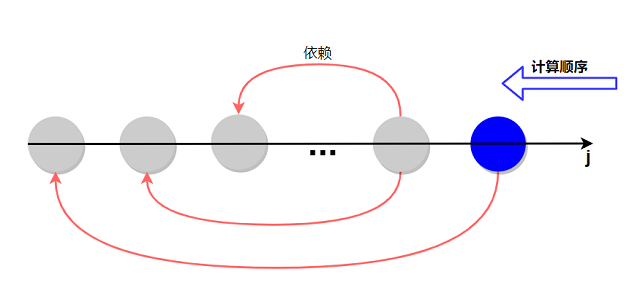
空间优化版本:

由于对$dp[i][\cdot]$对应状态仅仅依赖于$dp[i - 1][\cdot]$, 所以我们可以将$dp$数组降至一维: 每次
计算$dp[i][j]$时, 未更新前其值对应$dp[i - 1][j]$, 由此计算得到的值对应$dp[i][j]$. 由于$dp[i][j]$
可能会依赖$dp[i - 1]$对应较小体积$j’$($j’\lt j$)的状态, 为保证计算过程中依赖状态对应的是$i-1$时的
状态, 我们按$j$从大到小的顺序更新.

用灰色表示未更新状态, 蓝色表示更新状态, 简单说明$j$的计算顺序背后的含义.

对应代码:

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 1010;

int n, m;
int v[N], w[N];
int dp[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = m; j >= v[i]; j -- )
            dp[j] = max( dp[j], dp[j - v[i]] + w[i]); //max括号内部对应dp[i-1][]
    }
    cout << dp[m] << endl;

    return 0;
}

完全背包

状态表示 dp[i][j]

分析过程与01背包相同.

状态计算

对于状态$dp[i][j], $第$i$个物品数量$k$可选范围: $k\in [0,\lfloor \frac{j}{v_i}\rfloor]$.

为不失一般性, 考虑第$i$个物品选择$k$个的状态, $k\in [0,\lfloor \frac{j}{v_i}\rfloor]$ :
问题转变为: 从前$i - 1$个物品中选择且总体积不超过$j - k\times v_i$的所有选法.

• 固定部分: 第$i$个物品选择了$k$个, 其对应价值为$k\times w_i$.

• 可变部分: 根据定义, 其对应集合的最大值为$dp[i - 1][j - k\times v_i]$

为保持集合的Max属性, $dp[i][j]$保持上述所有集合最大值的最大. 当集合存在时思路同上: $\varnothing$,
其值可以认为是$0$.

代码实现

首先是根据上述分析得到的朴素版本.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 1010;

int n, m;
int v[N], w[N];
int dp[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 0; j <= m; j ++ )
        {
            for( int k = 0; k * v[i] <= j; k ++ )
            {
                dp[i][j] = max( dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i] ); 
            }
        }
    }
    cout << dp[n][m] << endl;

    return 0;
}

空间和时间的优化版本

首先考虑对时间的优化: 对于状态$dp[i][j]$和$dp[i][j-v_i]$, 其物品可选择的上限相同 : 设上限为$u$,
$u = \lfloor \frac{j}{v_i}\rfloor$. 有:

• $dp(i,j)=max( dp(i-1,j), dp(i-1,j-v_i)+w_i, dp(i-1,j-2v_i)+2w_i,..,dp(i-1,j-u\times v_i)+u\times w_i)$

• $dp(i,j-v_i)=max(\;\;\;\;dp(i-1,j-v_i), dp(i-1,j-2v_i)+w_i,,..,dp(i-1,j-u\times v_i)+(u-1)\times w_i)$

综合上式, $dp(i,j) = max( dp(i-1,j), dp(i,j-v_i)+w_i )$.

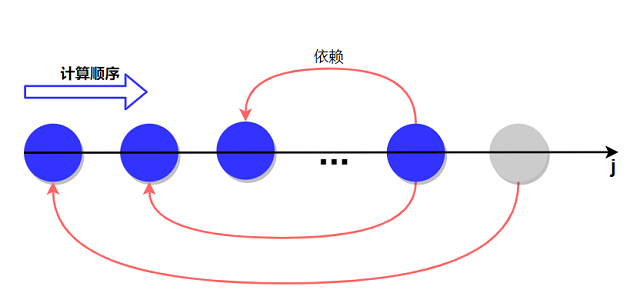
在此基础上考虑空间优化: 时间优化后$dp(i,j)$的计算方式与01背包类似, 所以空间优化的思路也类似.
不同点在于对于01背包, 其依赖的状态为$dp[i-1][\cdot]$, 而对于完全背包其依赖的状态为$dp[i][\cdot]$,
所带来的不同在于完全背包其$j$按从小到大的顺序更新.

用灰色表示未更新状态, 蓝色表示更新状态, 简单说明$j$的计算顺序背后的含义.

对应代码:

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 1010;

int n, m;
int v[N], w[N];
int dp[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = v[i]; j <= m; j ++ )
            dp[j] = max( dp[j], dp[j - v[i]] + w[i] ); //max括号内对应dp[i-1][j], dp[i][j-v[i]]
    }
    cout << dp[m] << endl;

    return 0;
}

多重背包

状态表示 dp[i][j]

分析过程与前两个背包问题相同.

状态划分

对于状态$dp[i][j], $第$i$个物品数量$k$可选范围: $k\in [0,min(\lfloor \frac{j}{v_i}\rfloor, s_i)]$. 其中$s_i$是题目对第$i$个物品可选数量的上限.

为不失一般性, 考虑第$i$个物品选择$k$个对于的状态, $k\in [0,min(\lfloor \frac{j}{v_i}\rfloor, s_i)]$ :
问题转变为: 从前$i - 1$个物品中选择且总体积不超过$j - k\times v_i$的所有选法.

到这里的分析与完全背包一致, 除了可选数量$k$的范围. 在朴素版本中这体现为对于$k$的循环判断
多了一个限制条件.

多重背包问题 I 朴素版本 $O(N\times V\times S)$

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110, M = 110;

int n, m;
int v[N], w[N], s[N];
int dp[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i] >> s[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 0; j <= m; j ++ )
        {
            for( int k = 0; k * v[i] <= j && k <= s[i]; k ++ )
            {
                dp[i][j] = max( dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i] );
            }
        }
    }
    cout << dp[n][m] << endl;

    return 0;
}

多重背包不能用完全背包的优化方式

两个背包问题的可选数量$k$的范围不同带来的另一个影响是多重背包不能用完全背包的优化方式优化.
$k\in [0,min(\lfloor \frac{j}{v_i}\rfloor, s_i)]$, 考虑一种情况: $k$只受到$s_i$的限制, 那么:
对于状态$dp[i][j]$, 其依赖状态为: $dp[i-1][j\sim j - s_i\times v_i]$; 而对于状态$dp[i][j-v_i]$,
其依赖状态为: $dp[i-1][j\sim j - (s_i + 1)\times w_i]$, 所以此时对于$dp[i][j]$求最大值不能
使用$dp[i][j - v_i]$, 因为后者求最大值时可能等于多出的一项$dp[i-1][j - (s_i + 1)\times w_i]$.

多重背包问题 II 二进制优化 $O(N\times V\times \lg{S})$

优化思路: 将多重背包问题-->$01$背包问题, 最重要的问题是如何快速的遍历$0\sim s_i$的所有数目的选择.
我们可以将$s_i$拆成$s_i$份, 当然这就是朴素版本, 没有带来时间上的优化; 实际上我们可以用二进制的思路
优化:

• 例如$s_i=7$, 可以遍历物品$(v_i, w_i), (2v_i,2w_i), (4v_i,4w_i)$. 因为$01$背包会考虑所有物品选
  或者不选两种可能, 在这个过程中我们就把$0\sim 7$的所有二进制形式遍历了一遍.

• 考虑更一般的情况, 将$s_i$划分为$1, 2, \cdots , 2^k, c$. 其中$c = s_i-(2^{k+1}-1), c\lt 2^{k+1}$.
  对于$0\sim 2^{k+1}-1$,我们在遍历$1\sim 2^k$物品选或不选的过程中把所有对应的二进制形式
  遍历的一遍, 当我们选择$c$时, 又把$c\sim 2^{k+1}-1+c$即$c\sim s_i$的二进制形式遍历了一遍,
  而$c\lt 2^{k+1}-1$, 所以两个范围的交集为$0\sim s$.

代码实现:

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010 * 11, M = 2010;

int n, m;
int v[N], w[N];
int dp[M];

int main()
{
    cin >> n >> m;

    int cnt = 0;
    for( int i = 1; i <= n; i ++ )
    {
        int a, b, s; //v, w, s
        cin >> a >> b >> s;
        int k = 1;
        while( k <= s )
        {
            cnt ++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if( s )
        {//此时s = c
            cnt ++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }

    n = cnt; //转为01背包问题
    for( int i = 1; i <= n; i ++ )
    {
        for( int j = m; j >= v[i]; j -- )
            dp[j] = max( dp[j], dp[j - v[i]] + w[i] );
    }
    cout << dp[m] << endl;

    return 0;
}

考虑多重背包每个物品$i$都有$s_i$的上限, 可以用滑动窗口类似的思路优化.

多重背包问题 III 单调队列优化 $O(N\times V)$

考虑状态$dp(i, j)$且数量限制考虑$s_i$(加一个条件判断是否超过体积限制), 那么其依赖的状态为:
$dp(i - 1, j - s_i\times v_i\sim j)$; 而对于状态$dp(i, j-v_i)$, 其依赖的状态为$dp(i - 1,j - (s_i+1)\times v_i)\sim j - v_i$, $\cdots$

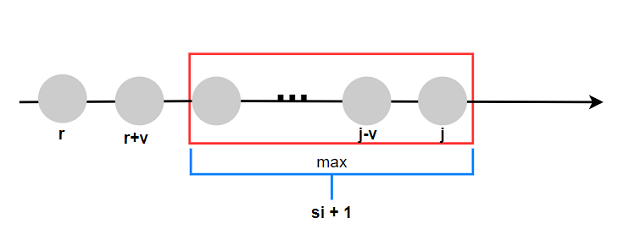
对于$dp(i, j-k\times v_i)$类型的状态, 它们具有一个相同性质:

$\;\;\;\;(j - k\times v_i)\% v_i = j \% v_i = r $.

也就是说, 对于第$i$个物品的状态: $dp(i, 0\sim V)$, 可以用$\% v_i$的形式将这些状态分为$v_i$类,
每一类对应模$v_i$余数$r$为$0\sim v_i-1$. 而对于某一类内部的状态, 其仅依赖同一类状态中$dp(i-1,j-s_i\times v_i\sim j)$, 实际上是依赖于长度最大为$s_i+1$的一个窗口内的最大值:

用灰色表示$i-1$对应状态, 下图表示$dp(i,j)$依赖的状态:

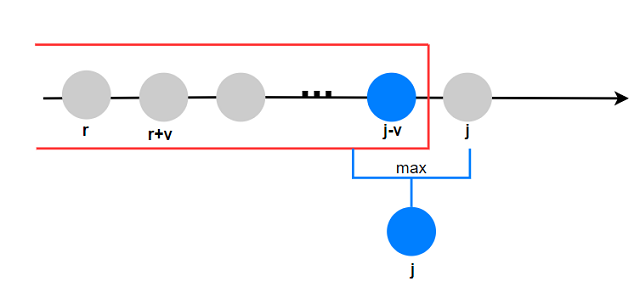
暂时跳出本题, 回想完全背包问题, 完全背包问题中对于状态$dp(i,j)$, 其依赖的状态为$dp(i-1,r\sim j)$,
即求的不是一个固定窗口大小为$s_i+1$的最大而是前缀最大, 其中$r = j\% v_i$

下图展示完全背包的优化思想: $dp(i,j-v_i)$已经计算了前面状态的前缀最大, 所以有我们得到的优化公式

回到本题, 对于每一类求滑动窗口最大值, 可以应用 单调队列 解决.

代码实现

注意: 之前的分析没有考虑对于状态$dp(i,j)$其考虑$dp(i,j-k\times v_i)$时需要加上$k$个
第$i$个物品的价值$k\times w_i$. 这里实现时单调队列保存的是$i-1$状态对应的体积大小. 所以
在取出队列中元素时需要加上$(j-x)/v_i * w_i$, 其中$x$为队列中保存的体积大小.

二维空间实现

理解的关键是单调队列中保存的是$i-1$对应状态的体积.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 20010;

int n, m;
int w[N], v[N], s[N];
int dp[N][M];
int q[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i] >> s[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int r = 0; r < v[i]; r ++ )
        {//每个余数对应一类
            int tt = -1, hh = 0;
            for( int j = r; j <= m; j += v[i] )//遍历每一类所有状态
            {
                while( hh <= tt && ( j - q[hh] ) / v[i] > s[i] )    hh ++ ; //滑出窗口
                while( hh <= tt && dp[i-1][j] > dp[i-1][q[tt]] + (j - q[tt]) / v[i] * w[i] ) tt --;
                q[++ tt]  = j;
                dp[i][j] = dp[i - 1][q[hh]] + ( j - q[hh] ) / v[i] * w[i];
            }
        }
    }
    cout << dp[n][m] << endl;

    return 0;
}

一维优化

因为$dp(i)$可能用到$dp(i-1)$一段窗口的值, 所以不能直接用01背包的空间优化方式. 需要用到两个数组,
$g$用来保存$dp(i-1)$的状态. 实现时只要将$dp(i-1)$对应的代码用数组$g$代替即可.

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 20010;

int n, m;
int w[N], v[N], s[N];
int dp[M], g[M];
int q[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i] >> s[i];

    for( int i = 1; i <= n; i ++ )
    {
        memcpy(g, dp, sizeof dp);
        for( int r = 0; r < v[i]; r ++ )
        {//每个余数对应一类
            int tt = -1, hh = 0;
            for( int j = r; j <= m; j += v[i] )//遍历每一类所有状态
            {
                while( hh <= tt && ( j - q[hh] ) / v[i] > s[i] )    hh ++ ; //滑出窗口
                while( hh <= tt && g[j] > g[q[tt]] + (j - q[tt]) / v[i] * w[i] ) tt --;
                q[++ tt]  = j;
                dp[j] = g[q[hh]] + ( j - q[hh] ) / v[i] * w[i];
            }
        }
    }
    cout << dp[m] << endl;

    return 0;
}

这里如果觉得本题解释不够清晰, 推荐@彩色铅笔的题解.