正常发挥，最近太懈怠了。。。学算法和学校的事情没平衡好
第一题暴力即可 第二题排序完二分 第三题dp或转化为组合数问题
T1：
暴力 从a+1开始枚举 符合后面不超过b个人的就是合法位置 枚举到n

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
//排在他前面的人不少于 a 个，排在他后面的人不超过 b 个
int t,n,a,b;
int main()
{
    cin>>t;
    while (t--){
        cin>>n>>a>>b;
        int u=0;//u存合法位置数
        for (int i=a+1;i<=n;i++){
//从a+1开始枚举 若排该位置 后面的人不超过b个则合法
            if (n-i<=b) u++;
        }
        printf ("%d\n",u);
    }
    return 0;
}

T2：
若无梁子 则对于战士而言只要比他战斗值低的就都可以做他徒弟 那么就是求比他弱的人数。
有仇的情况下，对于战斗力高的战士而言，他的徒弟名额就减一。
所以对于战力为a[i]的战士来说，他徒弟的数量就是，比他弱的人-比他弱还有梁子的人的数量

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
// 所以对于战力为a[i]的战士来说,他徒弟的数量就是
// 比他弱的人-比他弱还有梁子的人的数量
// 比他弱的人可以排序后二分得到 
// 比他弱还有梁子的人在读入时做好标记
const int N = 2e5+10;
int n,k,a[N],d[N],g[N];
//a存战斗力 d存比战士i弱还有梁子的人 g存储排序后的战斗力
int find_l(int x){//二分模板一 返回左边界的下标
    int l=1,r=n;
    while (l<r){
        int mid=l+r>>1;
        if (x<=g[mid]) r=mid;
        else l=mid+1;
    }
    return l;
}
int main()
{
    cin>>n>>k;
    for (int i = 1; i <= n; i ++ ){
        scanf ("%d",&a[i]);
    }
    memcpy(g,a,sizeof a);
    sort(g+1,g+1+n);
    for (int i = 1; i <= k; i ++ ){
        int x,y;
        scanf ("%d%d",&x,&y);
        if (a[x]>a[y]){
            d[x]++;//比他弱还有梁子的人在读入时做好标记
        }
        if (a[x]<a[y]){
            d[y]++;
        }
    }
    for (int i = 1; i <= n; i ++ ){
        printf ("%d ",find_l(a[i])-d[i]-1);
//find_l(a[i])返回排序后比a[i]弱的人 
//d[i]比战士i弱还有梁子的人
//由于是从1开始存储 所以记得-1
    }
    return 0;
}

T3
dp或转化为组合数问题
法1：转化为组合数问题
难在思维，对于数组a要求不严格递增，对于数组b要求不严格下降，同时要求a[i]<=b[i]
如此看来 只要看合法的两个数组，是否满足a[m]<=b[m]，那么便是一个合法的数组对
此时 对于合法数组对，反转b数组，就会成为一个长度为2*m的非严格递增子序列。

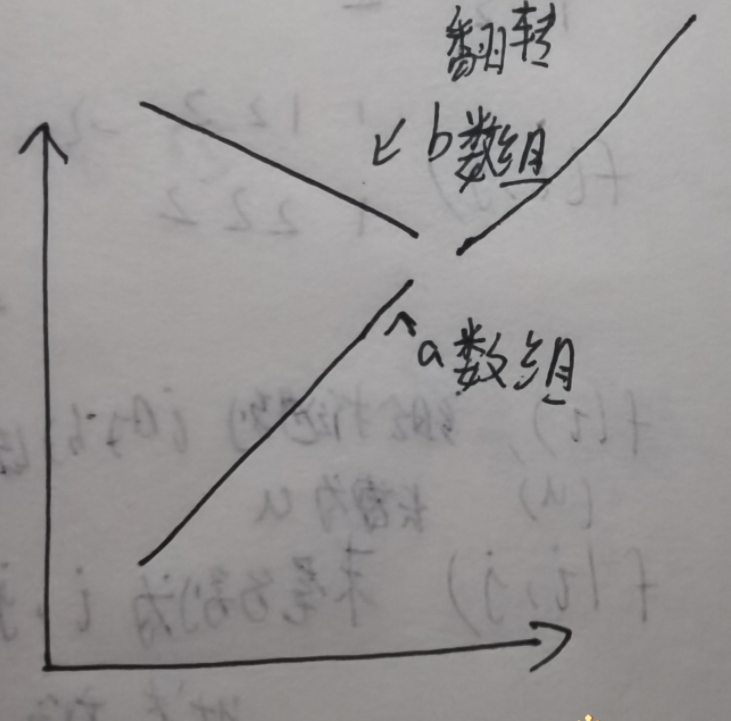
那么 我们就可以将问题转换为 2m个数从1~n中取，可以组成多少个不同的序列
@irrational大佬的题解中将其视为一个放球问题。
将2m个无区别的球放在n个顺序排列的箱子中，问有几种放法，允许都放一个箱子，允许空箱。
那么，运用隔板法，就可以解决问题。将n个箱子视作n-1个隔板，在2m个球中间放置。
那么就可以视作是，在2m+n-1个位置上，选择n-1个位置作为隔板。
那么取法就是$C_{2m+n-1}^{n-1}$个。
所以$C_{2m+n-1}^{n-1}$就是答案。
综上，在1~n个数中，能构造出多少个长为m的数对,$C_{2m+n-1}^{n-1}$就是答案。
ps:本题数据范围不大，就用$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$的公式了

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int mod=1e9+7;
int n,m;
int f[2050][2050];
void init(){
    f[0][0]=1;
    for (int i=1;i<=2000;i++){
        f[i][0]=1;
        for (int j=1;j<=i;j++){
            f[i][j]=(f[i-1][j-1]+f[i-1][j])%mod;
        }
    }
}
int main()
{
    cin>>n>>m;
    init();
    cout<<f[2*m+n-1][n-1];
    return 0;
}

法2：
我自己的超时了，还在研究光头哥的题解2333
摆烂 放个大佬的题解吧peter佬
光头哥